3.3 The Generator

Section 3.2 asks the reader to assume that the table is built by magic. The truth is that translating regular expressions to a state table or case statement is more tedium than magic. In this section, we will outline the steps and leave the algorithm to the reader (see Exercises 7 to 9 ).

Lexical Analyzer Generator Step 0: Recognizing a Regular Expression

A regular expression is either:

1. empty (null) , representing no strings at all, denoted by
2. denoting the language consisting of the empty string (Sometimes 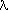is used to denote the empty string and the associated regular expression.)
3. a single letter e.g., a representing the language consisting of an a.
4. the union of two regular expressions a and b, denoted by a | b (also sometimes denoted by a + b or a U b )
5. the concatenation of two regular expressions a and b, denoted by a b (often the is omitted").
6. the Kleene closure. which is the union of with a, with a a, with a a a, etc. and denoted a*.

   a* = {} U a U a a U a a a U ...

   To convert a regular expression to a finite automaton requires the recognition of , |, * and as well as the individual characters in the sets. Recognition of is not really possible, so the resulting automaton will have to be converted to one which has no

   - transitions.

   Converting a Regular Expression to a Finite Automaton

   Converting from an NFA to a DFA

   Converting to a Minimal DFA

   

   Send questions and comments to: Karen Lemone