3.3.1 Lexical Analyzer Generator Step 1:
Converting a Regular Expression to a Finite
Automaton

There are six steps (a) - (f):

The diagram above shows that the regular expression is recognized by a nondeterministic finite automaton that has no way to get to a final state.

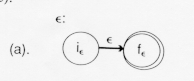
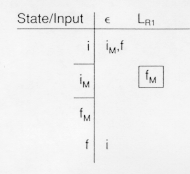
The diagram above shows that the regular expression is recognized by the nondeterministic finite automaton which goes from its initial state to its final state by reading no input. Such a move is called an - transition

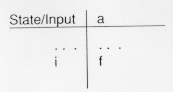
In table form this would be denoted:

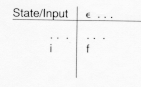
The reader may be wondering about an input of and how it would be recognized by the driver. In fact, it will not be. This is just a first step in table creation, and we will allow the creation of a nondeterministic finite automation (NFA). Section 3.3.2 outlines how to turn this NFA into a deterministic finite automation (DFA)

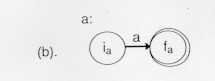
The diagram above shows that the language {a} denoted by the regular expression a is recognized by the finite automatation that goes from its initial to final state by reading an a. In table from this would be:

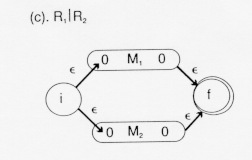
In the diagram above, we presume that the languages denoted by the regular expressions R and R, respectively, are recognized by the finite automata denoted by M and M.

Adding -transitions to the beginning and end creates a finite automation which will recognize either the language represented by R or the language represented by R, i.e., the union of these two languages, LR U LR.

We could eliminate the new final state and the -transitions to it by letting the final states of M and M remain final states.

In table form, this is:

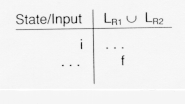
Here, the table entry for f is shown in a different row because the process of recognizing strings in either LR or LR may lead to other intermediate states.

Our example, which recognizes

Letters = A | B | C | . . . | a | b | . . . |z

and Literal = 0 | 1 | 2 | . . . | 9

will use this step.

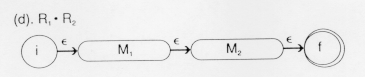
In the diagram above, M is the machine that accepts LR and M is the language that accepts LR. Thus, after this combined automation has recognized a legal string in LR, it will start looking for legal strings LR. This is exactly the set of strings denoted by R R. The related table is:

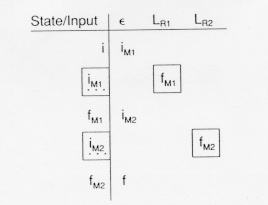
Here the table leads from an initial state, i, to the final state of M upon recognition of strings in LR, then from the final state in M, fM to the initial state in M on an -transition, that is, without reading any input, and then from the initial state in M, iM to the final state in M, fM upon recognizing the strings in LR. The is often omitted. It is understood that two regular expressions appearing next to one another represents the concatenation. We will use this step for the example, when we define an identifier as a string of letters and digits (conatenated). Another example will recognize a literal as the concatenation of one or more digits, that is,

Identifier = Letter (Letter | Digit) *

means

Identifier = Letter (letter | Digit) *

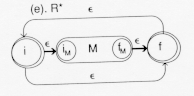
Here, M is a finite automation recognizing some LR. A new initial state is added leading to both M and to a new final state. The - transition recognizes the empty string, (if R did not contain already). The transition to M causes the language LR to be recognized. The transition from all final states of R to its initial state will allow the recognition of LR , i = 1, 2,... The table is:

We will use this step as well as the preceding two, for the regular expressions

Identifier = Letter (Letter | Digit)*

and

Literal = Digit* = Digit Digit*

Using these diagrams as guidelines, we can "build" a nondeterministic finite automation from any regular expression (See Exercise 6