3.3.2 Lexical Analyzer Generator Step 2:
Converting from an NFA to a DFA

As we saw in Section 3.3.1, an NFA may have transitions on reading no input. In addition, an NFA may have more than one transition from the same input:

In Figure 2, one can go from state 1 to either state 1 or state 2 upon reading a "$".

These two possibilities, -transitions and multiple transitions on the same input, represent nondeterminism.

To convert from an NFA to a DFA, we eliminate these two possibilities by grouping states in the NFA. A state in the DFA will consist of a group (set) of states from the NFA.

The new start state is the same as the old start state.

With the new start state we group all the states we can get to upon reading the same input in the NFA; this process is continued with all the states of the NFA that are in any set of states in the DFA.

Any state in the DFA that contains a final state of the NFA is a final state.

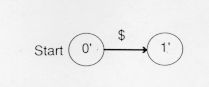
For the NFA above, the new start state is 0', the prime to distinguish it from the old start state. State 1' = {1} since the only state accessible from state 0 in the NFA is state 1:

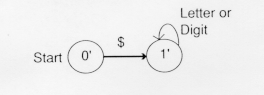
The situation is different for transitions from 1'={1}. Upon reading a letter or a digit, the transition is back to state 1. We can add that transition to the DFA:

But there are two transitions upon reading "$" in the NFA, a move to state 1 and a move to state 2. We group these states into a new state called 2'={1, 2} in the DFA.

The DFA now is:

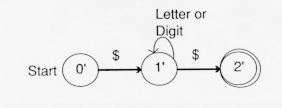
The state 2'={1,2} contains the old final state 2, so it is a final state.

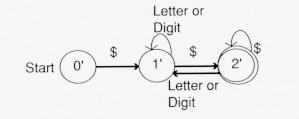
If we are in state 2', so it is a final state. If we are in state2' = {1, 2} and the input is a letter or a digit, there is a transition back to 1' (because there is a transition from 1 to 1 in the NFA). Finally, there is a transition from 2' to 2' in the DFA upon reading a $ ( because there is a transition from 1 to 1 upon reading a $ in the NFA and 2'={1, 2}). The final DFA is:

This step of the lexical analyzer generator, conversion of a regular expression to a DFA, has shown the automata in the state-transition form. This could equally well have been shown in table form (See Exercise 7).

The step for removing -transitions is similar; all the states accessible via an -transition are grouped (See Exercise 6). This step can frequently result in DFA's with many states, some of which are performing the same function and can be combined. This is a necessary step in generating a lexical analyzer since there may be hundreds of states in the table for the tokens in a programming language.

A purist would not consider the above automation a true DFA since a true DFA will have a transition somewhere upon reading any character in the alphabet. Thus, state 0' should have an arrow (leading to an "error" state) upon reading a letter or a digit.