Basic Blocks

Building a Flow Graph

Techniques for Building Flow Graphs

Data Structures for Building Control Flow Graphs

DAGs

Data Structures for a DAG

Benefits of DAGs

When a DAG is created, common subexpressions are detected. Also, creating a DAG makes it easy to see variables and expressions which are used or defined within a block.

DAGs also produce good code at code generation time. In Module 11, we will see a code generation algorithm which produces good (but not optimal!) code from a DAG.

Example 6 shows a bubble sort procedure and a set of quadruples to which it might be translated. Quadruples are an intermediate representation consisting of a single operation, up to two operands and a result. They are easier for humans to read than an abstract syntax tree. The quadruples shown here are in "assignment statement" form.

 EXAMPLE 6 IR for a bubble sort procedure
 	FOR I := 1 TO n - 1 DO
 	        FOR J := 1 TO I DO
 		IF A[J] > A[J+1] THEN
 		    BEGIN
 			Temp := A[J]
 			A[J] := A[ J + 1 ]
 			A[ J + 1 ] := Temp
 		    END
 
 	
 		
 		I := 1
 		GOTO ITest
 	ILoop:	J := 1
 		GOTO JTest
 	JLoop:	T1 := 4 * J
 		T2 := A [T1] 		; A[J]
 		T3 := J + 1
 		T4 := 4 * T3
 		T5 := A[T4] 		; A[ J + 1 ]
 		IF T2 <= T5 GOTO JPlus
 		T6 := 4 * J
 		Temp := A[T6] 		; Temp := A[J]
 		T7 := J + 1
 		T8 := 4 * T7
 		T9 := A[T8] 		; A { J + 1 ]
 		T10 := 4 * J
 		A[T10] := T9 		; A[J] := A[ J + 1 ]
 		T11 := J + 1
 		T12 := 4 * T11
 		A[T12] := Temp		; A [ J + 1 ] := Temp
 	JPlus:	J := J + 1
 	JTest:	IF J < = I GOTO JLoop
 	IPlus:	I := I + 1
 	ITest:	IF I <= n - 1 GOTO ILoop
 

The intermediate code shown in Example 6 is rather high-level. For machines which have no indexing modes, the references to A[...] will have to be computed by the compiler. Also, the IF statements really involve several quadruples (see Module 6). The multiplication by "4" could, alternatively, be done at code generation time. We do it here because it will give us more opportunities for optimization of our example.

Using "( )" to mean "contents of " and "addr" to mean "address of", the low-level quadruples for "Temp := List[i]" might be:

 	T1 := addr(List)
 	T2 := T1 + I
 	temp := (T2)
 

Similarly, if the array reference is on the left-hand side of an assignment statement as in "List[i] := temp", low-level quadruples would be:

 	T1 := addr (List)
 	T2 := T1 + I
 	(T2) := Temp
 

Even if a machine has an indexing addressing mode, translating array references into their low-level format may allow optimizations (for example, if the subscript reference were a common subexpression).

Nevertheless, there will be numerous opportunities to improve the code sequence in Example 6.

---

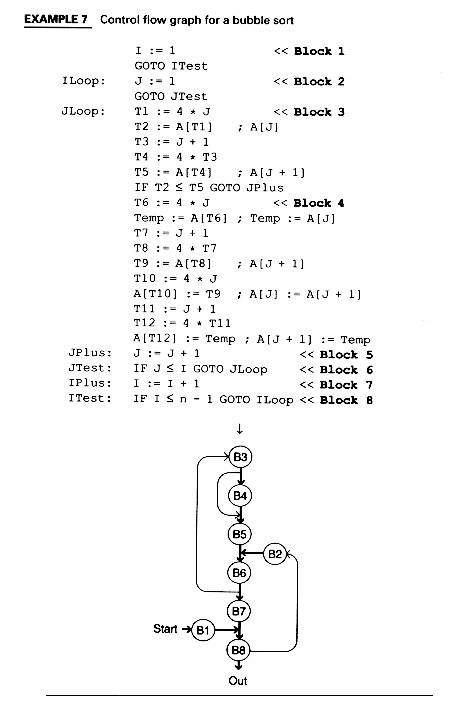
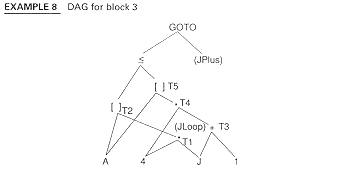
The program of Example 7 contains cycles which may be loops. Determining loops is a major activity of control flow analysis. Creating basic blocks and a control flow graph are two steps toward this process. In the next section, we will formalize the process of determining a loop in a control flow graph.

---