| 6.0 Introduction
6.4 Semantic Analyzer Generators |
6.3.3 Three-Address Code
This intermediate form is called three-address because each "line" of code contains one operator and up to three operands, represented as addresses. Since most assembly languages represent a single operation in an instruction, three-address code is closer to the target code than the parse tree representation. There are a number of variants of three-address code, some more appropriate than others for optimization.
Quadruples (A Three-Address Code)
Quadruples ("quads" for short) consist of an operation, (up to) two operands, and a result.
A + B would be translated into quads as:
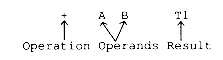
A + B * C would be translated into two quads:
* B C T1
+ A T1 T2
and S := A + B * C would be:
* B C T1
+ A T1 T2
= T2 _ S
Notice that the last quad here had only one operand rather than two.
An alternative notation for quads, one we will use in the chapters on optimization, is to write them as a sequence of assignment statements. Thus S = A + B + C would be written:
T1 = B * C
T2 = A + T1
S = T2
If we think of GOTO L as an operator and a result, the quad would be:

A[i] := B would be:
[ ] A I T1
= T1 _ B
The reasoning for the intermediate code for IF statements is similar to the reasoning used to implement such constructs into assembly language. For example, IF A<B THEN Max := B would be:
< A B Label 1
GOTO Label 2
Label 1
= B Max
Label 2
Here, the first line can be thought of as "if A<B then execute the code at Label 1". The second line can be thought of as "Otherwise execute the code at Label 2". The third line has only a result field--Label 1. These lines can be translated easily into assembly language code.
Triples(A Three-Address Code)
Quadruples use a name, sometimes called a temporary name or "temp", to represent the single operation. Triples are a form of three-address code which do not use an extra temporary variable; when a reference to another triple's value is needed, a pointer to that triple is used. We show the same examples as above for triples:
A + B would be translated into triples as:

A + B * C would be translated into two triples:
(1) * B C (2) + A (1)
Here, the triples have been numbered and a reference to the first triple is used as an operand of the second. S := A + B * C would be
(1) * B C (2) + A (1) (3) = S (2)
Triples are really an abstract syntax tree in disguise:
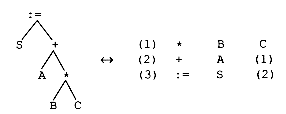
Triples are difficult to optimize because optimization involves moving intermediate code. When a triple is moved, any other triple referring to it must be updated also. A variant of triples called indirect triples is easier to optimize.
Indirect Triples(A Three-Address Code)
Here, the triples are separated from their execution order:
Triples:
1. * B C
2. + A (1)
3. = S (2)
Execution order: 1, 2, 3
Since the execution order here is the same as the order of the triples themselves, it is difficult to see the use of indirect triples. Example 3 shows a case where the execution order is not the same as the order of the indirectriple list.
With indirect triples, optimization can change the execution order, rather than the triples themselves, so few references need be changed.
EXAMPLE 3 Optimizing indirect triples
for i:=1 to 10 do <-> a:=b+c
begin (optimize) for i:=1 to 10 do
a:=b*c; begin
d:=i*3; d:=i*3
end end
. .
. .
end; end;
The triples for the original unoptimized version might be:
(1) := 1 i
(2) * b c
(3) := (2) a
(4) * 3 i Execution Order: 12345678
(5) := (4) d
(6) + l i
(7) LE I 10
(8) IFT go (2)
If the computation a:=b*c is moved out of the loop, as in the righthand optimized version, the execution order is 23145678. Notice that only the reference in (8) need be changed.
As an indication of how intermediate form might be generated during parsing, Section 6.3.6 describes how to generate abstract syntax trees during recursive descent parsing. Similar (semantic) routines would be written for generating AST's if the parser were generated using a tool. Most tools allow such routines to be written.
![]()