CS 2223 Mar 30 2023

Lecture Path: 10
Back Next

1 Hashing With Separate Chaining

1.1 Homework1

The average HW1 (for those students who submitted an assignment) for the past few offerings is:

• 2015 - 87.5

• 2018 - 91.5

• 2019 - 83.2

• 2020 - 82.0

• 2021 - 87.6

• 2022 - 75.8

• 2023 - 90.2 **

Within the expected range of experience.

Note that Rubrics for HW2 are now posted.

1.2 Lecture

For one wild, glad moment we snapped the chain that binds us to earth, and joining hands with the winds we felt ourselves divine...

The Story of My Life
Helen Keller

The Symbol Table (introduced last lecture) represents the ability to store a collection of values to be associated with a given key. The initial implementation stored all (key, value) pairs in a single linked list. This leads to inefficient performance when an increasing number of elements are being stored.

Specifically, when retrieving (get) or inserting (put) a value into the Symbol Table, the performance was directly proportional to the number of elements already stored by the Symbol Table.

We need some way to reduce the length of the linked lists. One solution that works very well in practice is to use a hash function to uniformly partition the keys into different linked lists. This is the intuition and basis for Hashing.

So we start not with a single linked list, but an array of SequentialSearchST objects as we introduced in last lecture. The question remains, however, as to how to partition the keys. The common way to do this is to develop some hashCode method that returns an integer based on the contents of a specific value.

The following is a sample hashCode method for the java.lang.String class:

public int hashCode() { int h = hash; if (h == 0 && value.length > 0) { char val[] = value; for (int i = 0; i < value.length; i++) { h = 31 * h + value[i]; } hash = h; } return h; }

This computed hash value is not guaranteed to be unique. There may be multiple keys that hash to the exact same value. However it is essential that if two key values are equal to each other, then they produce the same hash code.

Hello gives 69609650 aaaaaa gives -1425372064

As you can see, sometimes hashCode returns a negative number, because of mathematical overflow – note that hashCode returns an integer.

Now comes the premise, if this hashCode method does a good job in generating uniform integers, then you can create separate SequentialSearchST objects into which to add the (key, value) pairs. But how many objects should we create initially? Instead of worrying too much about that question, start with an initial number, and then resize as needed if the performance begins to suffer.

public class SeparateChainingHashST<Key, Value> { int N; // number of key-value pairs int M; // hash table size SequentialSearchST<Key, Value>[] st; // array of symbol tables int INIT_CAPACITY = 4; // initial size int AVG_LENGTH = 7; // Threshold to resize /** Initialize empty symbol table with <tt>M</tt> chains. */ public SeparateChainingHashST(int M) { this.M = M; st = (SequentialSearchST<Key, Value>[]) new SequentialSearchST[M]; for (int i = 0; i < M; i++) { st[i] = new SequentialSearchST<Key, Value>(); } } /** Choose initial default size. */ public SeparateChainingHashST() { this(INIT_CAPACITY); } /** Convert hashCode() into index between 0 and M-1 */ int hash(Key key) { return (key.hashCode() & 0x7fffffff) % M; } public int size() { return N; } public boolean isEmpty() { return size() == 0; } public boolean contains(Key key) { return get(key) != null; } public Value get(Key key) { int i = hash(key); return st[i].get(key); } public void put(Key key, Value val) { // double table size if average length of list >= AVG_LENGTH if (N >= AVG_LENGTH*M) resize(2*M); int i = hash(key); if (!st[i].contains(key)) N++; st[i].put(key, val); } }

After a few insertions into a table with M=6 separate chains (you might hear me say the word "bin" or "bucket" since those are common in the literature) you could have the following situation:

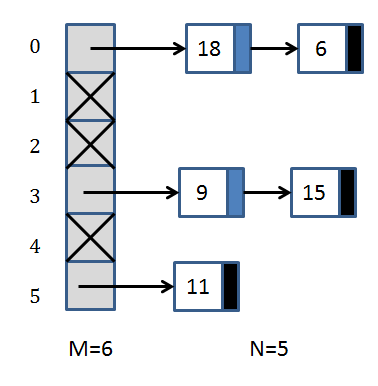
In this case, the hash function is simply "compute modulo 6 of the value being inserted".

1.3 How To Scale

Assuming that the hash uniformly distributes key values, this code improves the performance of each operation.

Specifically, when retrieving (get) or inserting (put) a value into the Symbol Table, the performance is now directly proportional to N/M

However, if you do nothing to change the number of M separate chains, you will eventually have decreasing performance, because N will be substantially greater than M.

Much like you have seen before, you need to resize the array of separate chains. However, what to do with the elements that have already been placed into the hash table? It turns out that you have to take a substantial performance penalty hit and reinsert all elements in the hashtable because they may end up in a different index because the value of the hash function is dependent on M.

The following resize method takes advantage of the existing constructor to simplify its implementation. Once done, it updates the st[] array to use the newly created one.

void resize(int chains) { SeparateChainingHashST<Key, Value> temp = new SeparateChainingHashST<Key, Value>(chains); for (int i = 0; i < M; i++) { SequentialSearchST<Key,Value>.Node node = st[i].first; while (node != null) { temp.put(node.key, node.value); node = node.next; } } M = temp.M; N = temp.N; st = temp.st; }

1.4 Demonstration

If you run the SeparateChainingHashST sample code, you will see the following output:

2015 213557 words in the hash table. Table has 45056 indices. there are 392 empty indices 99.1299715909091% maximum chain is 16 number of single is 1841 THIS YEAR 321129 words in the hash table. Table has 49151 indices. there are 79 empty indices 99.8392708184981% maximum chain is 19 number of single is 473

Note the average number one would expect in a chain is 213557/45056 (4.74) in 2015, or 321129/49151 (6.5) this year, which is impressive!

These results are incredibly promising! You can determine if an item exists in the Hash Table using no more than 19 comparisons. Of course, the memory requirements are noticeable, but you have to admit this is very nice.

Let’s look at these numbers in a bit more detail:

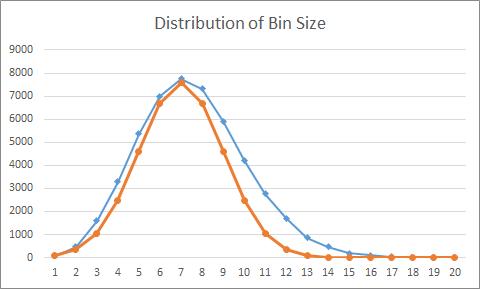
In this chart, the x-axis represents the size of an individual chain, and the y-axis counts then number of chains in the Hash Table with this given size. The blue line represents the actual results, while the orange curve models a normal distribution with a mean of 6 and stdev of 2.

As you can see there is a "longer tail" on the actual results, which suggests the normal distribution undercounts the number of chains that are long.

There is a direct comparison to make with using Binary Array Search over a sorted array. First, you would have to sort all strings and construct an array for them. Thereafter, the maximum number of comparisons to locate an entry would be 1 + Floor(log 321129) or 1 + Floor(18.29279) = 19.

This exercise demonstrates that using additional space can help improve performance.

1.5 Bad Hashing

What if the hash doesn’t do a good job in distributing the values? For example, consider hashing based solely on the first character of the String key value:

public int hash(Key key) { return ((String) key).charAt(0) % M; }

This would result in:

Elapsed time 110.77 seconds 321129 words in the hash table. Table has 49151 indices. there are 49125 empty indices 0.05289821163353414% maximum chain is 34638 number of single is 0 size distribution:[49125, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] number of excessive:26

1.6 Accounting BinaryArraySearch inspections

We have only referred to "log N + 1" for number of comparisons to make when performing Binary Array Search on an ordered collection of N values.

What if N is not a power of 2? The formula changes just slightly, to be 1 + Floor(log N)". In fact, the worst case for Binary Array Search occurs when N is exactly a power of 2 and the best case occurs when N=2k-1. It’s all in the mathematics.

1.7 Counting #less for Merge Sort

When reviewing the fine-grained behavior of MergeSort, there is "noise" in the data, which can be eliminated by focusing on problem instance input sizes where N is a power of two.

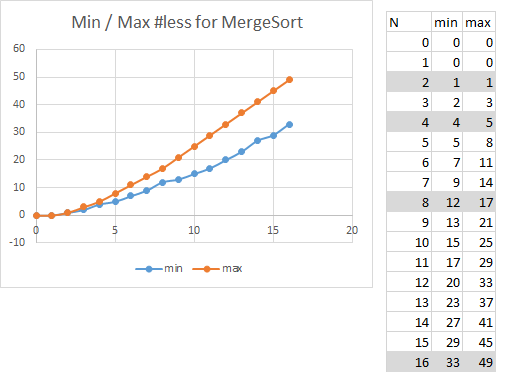
Look at the selected regions for N=2k and you can see that the empirical results confirm the following formula for N >=4. The most number of less comparisons used by Merge Sort is N*log(N)-N+1. What is the big O notation for this formula? Since N*log(N) will dominate the subtraction of N, the growth for this formula is O(N log N).

1.8 Improved O(...) Explanation

Let me try to explain why I focus my attention on key operations. In general, I am interested in the worst case for an algorithm. Let’s go further. For this worst case, I am interested in determining the number of "fundamental machine operations" based on the problem size N. This is incredibly hard! Don Knuth – a towering figure in algorithm analysis – created a hypothetical computer with 4000 bytes of RAM, he called MIX and meticulously designed implementations for key algorithms using this computer and he computed accurately the number of MIX operations executed for each algorithm he had designed. In this manner, MIX is like the Fruit Fly example from day 1 – a model computer which can be used to capture real-world examples that can be exactly analysed.

We don’t have that luxury, since we are programming in Java (an interpreted language) and so we can never know exactly how many fundamental computing operations are invoked.

So what do I do instead? I focus on specific key operations and count how many times these key operations are invoked for a problem instance of size N. Once you know that the total number of times less is invoked is equal to 3 * N * log(N) + 18 * N, then you know that the total number of operations is at least this amount.

The next observation is based on one that I have mentioned in class: when classifying an algorithm as O(N) I said that the performance of the algorithm is directly proportional to N, the size of the problem instance. Whether the number of operations is 15*N or 22*N + 18 or 1,028 * N, in all cases, the classification used is O(N) since in all cases, as N increases over tie, the performance is directly proportional to N.

By focusing a key operation, I make the hypothesis that for every key operation there is a constant number of individual machine operations that are executed. These operations are simple if statements, or variable declarations and expressions.

Sometimes when we do O() anlaysis, the goal is to analyze running time performance.

Sometimes we count the number of key operations. Other times, we look at space utilization.

1.9 Sample Exam Question

A researcher proposes to design a data type which consiststs of a linear linked list of nodes, each of which stores an array of K individual comparable items in sorted order. Only the last node in the list may contain fewer than K items. This data type will offer the following operations:

• insert (v) – insert v into the collection

• remove (v) – remove v from the collection

• contains(v) – check whether collection contains v

He claims he needs ~ log(N*K) performance for determining whether the collection contains a given element.

From this idea, there are several possible questions to ask:

• Start with the contains method. Come up with an algorithm for this method. What is the performance of your method?

• Is his performance claim correct?

• Write pseudo code for insert.

• Write pseudo code for remove.

1.10 Version : 2023/04/07

(c) 2023, George T. Heineman