CS 2223 Apr 15 2022

Lecture Path: 20
Back Next

Visual Selection: Peasant Woman Binding Sheaves, Vincent Van Gogh (1889)

Live Selection: Don’t Stop Believin’, Journey (1981)

Daily Question: DAY20 (Problem Set 20)

1 Quicksort

1.1 Main topics in sorting

Thou dost lie in’t,
to be in’t and say it is thine.
’Tis for the dead,
not for the quick;
therefore thou liest.
William Shakespeare
Hamlet

We have made some major progress in analyzing the sorting problem. We were able to assert the Mergesort is an asymptotically optimal compare-based sorting algorithm.

We made this claim because we demonstrated that any comparison-based sorting algorithm requires O(N log N) comparisons to correctly sort an array of N elements.

The logic was based on identifying a recursive formula that computed the number of comparisons required. We came up with the following formula that demonstrated the most number of comparisons that would be used.

C(n) <= C(n/2) + C(n/2) + N
C(n) <= 2*C(n/2) + N

Be sure you understand the logic as presented in lecture, which is supported by the book; review the class capture if that would be helpful.

1.2 Quicksort Implementation

At this point, you might ask why we should continue investigating sorting as a problem. Well, the first issue is that MergeSort still required O(N) extra storage with which to work. Is it possible to eliminate the extra overhead? It is, and the surprisingly brief implementation might stun you.

Find this implementation here: Quick.

public static void sort(Comparable[] a) { shuffle(a); sort(a, 0, a.length - 1); } // quicksort the subarray from a[lo] to a[hi] private static void sort(Comparable[] a, int lo, int hi) { if (hi <= lo) return; int loc = partition(a, lo, hi); sort(a, lo, loc-1); sort(a, loc+1, hi); }

Once again, you will note there are no comparisons or exchanges, so the real work appears to be done in partition. Just given the information above, let’s see if we can reverse engineer what the method is supposed to do.

It is instructive to compare this method with MergeSort:

mergesort(Comparable[] a, int lo, int hi) { if (hi <= lo) return; sort(a, lo, mid); sort(a, mid+1, hi); merge(a, lo, mid, hi); }

In MergeSort, both halves of the array are sorted, and then merged into place using auxiliary storage.

In Quicksort, an item in a[lo..hi] is found and put into its final spot at a location identified by loc. Let’s assume for a moment that this is even possible. Then, all you need to do is sort the left side a[lo..loc-1] and then the right side a[loc+1..hi].

Now, if partition is able to be effective at finding a value "near the middle" of the array, then the left and right sort subproblems will more or less be half the size of the original problem, and we will be able to demonstrate an asymptotically optimal compare-based sorting algorithm.

1.3 It’s all in how you partition it...

The speed and elegance of Quicksort comes from the partition method. Numerous methods have been proposed (there are at least four that I know of). The book lists one (p. 290) that is clean and easy to visualize. It also has some nice features that take advantage of duplicate values that might exist in the array.

First the intuition: Pick one of the existing values in a[lo..hi] and try to find where it belongs. For convenience, start with the value in a[lo]. Now, imagine sweeping through the array with two index values. Index left starts at lo and advances towards hi. While another index right starts at hi+1 and descends towards lo. Until these indices "cross each other" you try to find two elements that can be swapped with each other.

Let’s try to identify some truths in the following annotated code. The handout has the clean code, so the following is a bit verbose but it has everything you need to know.

These ten-lines of code have a number of complicated logical conditions in such a small space. You truly need to work out a number of examples BY HAND to make sure you are able to follow the logic. Page 291 of the book has a long example and I encourage you to review that example.

Let’s try our hand at the partitioning the following seven-member array:

Start as follows:

1.4 And now we see why shuffle is necessary

Quicksort is dependent on the selection of the partitioning element. As you will see on page 295, if the partitioning only reduces the problem size by 1 then the total number of compares will be O(N2), which was exactly the case for Selection Sort.

So the trick is to ensure the value choosed to partition is close to the median value, that is, the value in the list which has an equal number of items smaller than or equal to it as it does that are greater than or equal to it.

You might think that you need to sort a collection to find its median value, but it turns out there is an approach you can use to determine it in time directly proportional to the elements in the array. However it is not used in practice because of its complexity.

The advanced mathematics alluded to in the book declares that "on average" the partition will be about half, and in the long run, this will lead to a demonstrated number of comparisons that is 40% above optimum.

1.5 Weakness in this partition

Review what happens when all elements are the same!? That is, given an array of SEVEN elements, how does partition operate? And what value right is returned?

Start by selecting a[lo] as the element v to place, set left to lo and right to be one greater than hi:

Remember that the inner while loops use pre-increment for left and pre-decrement for right. In both cases, the condition is false because all values are the same, however left and right are both incremented. When we get to the exch within the while loop, the two values are exchanged, even though they are the same value. The resulting state is follows:

This will repeat three more times, with left and right finally crossing paths, thus terminating the loop. Naturally, during all this time, these exchanges are wasted.

But ask yourself whether it is worth your time to add an additional comparison just to ensure that the elements being swapped are different. Since you are trying to reduce the number of comparisons, it turns out not to help.

1.6 Quicksort Optimizations

The most common optimization for Quicksort include:

• Minimum size for recursion – if length of subarray to be sorted is smaller than some threshold (47 in Java JDK) then switch to insertion sort

• Pivot strategies – Dual-Pivot Quicksort algorithm by Vladimir Yaroslavskiy, Jon Bentley, and Josh Bloch. The algorithm offers O(n log(n)) performance on many data sets that cause other quicksorts to degrade to quadratic performance, and is typically faster than traditional (one-pivot) Quicksort implementations.

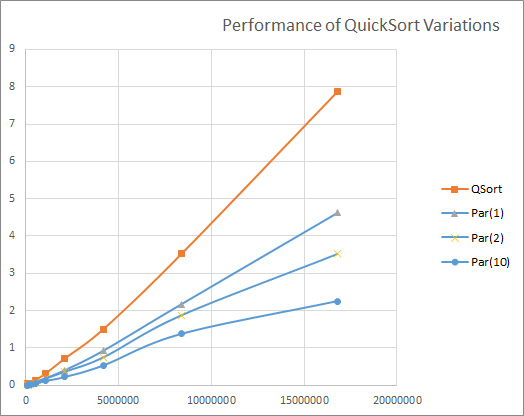
• Parallelize subtasks – Some improvement

  N QSort Par(1) Par(2) Par(10) 65536 0.0469 0.0156 0.0156 0.0000 131072 0.0156 0.0313 0.0000 0.0156 262144 0.0469 0.0313 0.0156 0.0156 524288 0.1250 0.0781 0.0625 0.0313 1048576 0.2969 0.1719 0.1719 0.1094 2097152 0.7031 0.3906 0.3594 0.2188 4194304 1.5000 0.9219 0.7500 0.5313 8388608 3.5156 2.1719 1.8750 1.3750 16777216 7.8594 4.6250 3.5156 2.2500

1.7 Lecture Key Topics

• MergeSort does not improve with increased duplicate values

• Quicksort suffers if partition only reduces problem by size 1. For this reason, the values are initially randomly sorted. Do you think this is a waste of time? Evaluate its performance as N exchanges, which can be easily absorbed by our expected O(N log N) performance.

1.8 Daily Question

The assigned daily question is DAY20 (Problem Set DAY20)

If you have any trouble accessing this question, please let me know immediately on Discord.

1.9 Version : 2022/04/19

(c) 2022, George T. Heineman