CS 2223 Apr 14 2022

Lecture Path: 19
Back Next

Musical Selection: UB40: Can’t Help Falling In Love (1993)

Visual Selection: The Starry Night, Vincent Van Gogh (1889)

Live Selection: White Rabbit, Jefferson Airplane, 1969

1 Expression Trees

Yoda: No more training do you require. Already know you, that which you need.
Luke: Then I am a Jedi.

Yoda: No. Not yet. One thing remains. Vader. You must confront Vader. Then, only then, a Jedi will you be. And confront him you will.
Star Wars: Episode VI

The Binary Tree structure can be used for other purposes. In this lecture, I will introduce a common usage, namely to store the representation of an expression.

We have already seen expressions represented using Infix and Postfix strings. Ultimately "(4 + 5)" and "4 5 +" are equivalent. It’s time to describe how to construct a binary tree structure that represents the mathematical expression, over which we can perform a number of operations (like evaluating or producing the infix/postfix notation).

Consider the following structure:

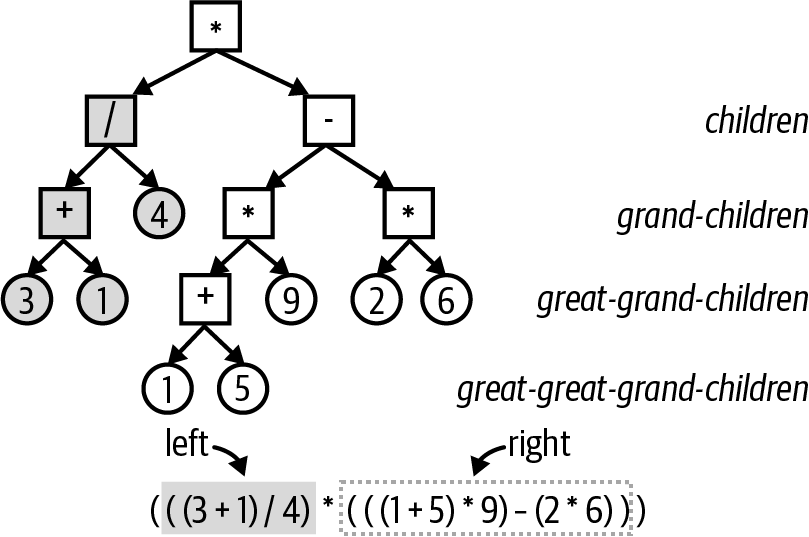
This sure looks like a binary tree. Observe the binary structure inherent in this expression. For simplicity, all operations considered are binary operations with two arguments.

The top multiply node has two child nodes, ultimately leading to four grandchild nodes (one of which is the value 4), six great-grandchild nodes, and two great-great grandchild nodes.

The expression represents the multiplication of two expressions, which demonstrates its recursive structure. To compute the value of this expression, first recursively compute the left expression to produce the result 1. In similar recursive fashion, the right expression evaluates to 42, so the overall result of the original expression is 1 * 42 = 42.

Evaluating an Expression is a recursive process that will eventually terminate at Value objects.

Expression one = new Multiply(new Value(2), new Value(3)); Expression two = new Sqrt(one); System.out.println("one:" + one.format()); System.out.println("two:" + two.format()); System.out.println(new Sqrt(new Value(2)).format()); System.out.println("two evaluates to " + two.eval());

The tree is constructed "from the leaves upwards" which is a distinctly different feel than when constructing a Binary Search Tree by inserting values.

Once you have an expression tree, there are lots of things you can do with it. I’ve shown the standard evaluation and "pretty print" operations. But look at the option which generates Java code statements to compute this expression:

double x0 = 3.0; double x1 = 1.0; double x2 = x0 + x1; double x3 = 4.0; double x4 = x2 / x3; double x5 = 1.0; double x6 = 5.0; double x7 = x5 + x6; double x8 = 9.0; double x9 = x7 * x8; double x10 = 2.0; double x11 = 6.0; double x12 = x10 * x11; double x13 = x9 - x12; double x14 = x4 * x13; System.out.println("value is " + x14);

1.1 Heap Sort

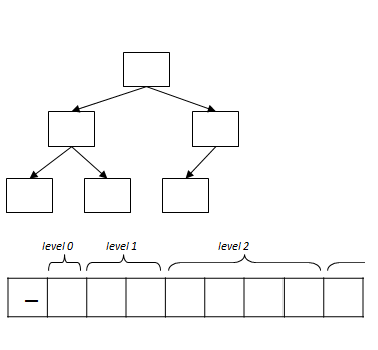
Use this process to build a heap after the following values have been added in the following order:

2, 7, 4, 9, 8, 6

Assuming the array has enough room for the elements, what will be the final array representation in the resulting heap?

1.2 How to use Heap to implement sorting

First observe that the topmost element of the heap is always the largest item. This gives us our first clue. However, if we are to sort "in-place" without any additional storage, what can we do?

Start with an arbitrary array and convert it into a Heap. Note that we now have to ensure that the 0th array location is part of the heap, which is something we didn’t do earlier; however, nothing could be simpler!

The trick is to recognize that all elements are refered to only within the less and exch methods. Therefore, these two methods are changed as follows to reflect 1-based indexing. Thus the 1st element is to be found at index location 0.

static boolean less(Comparable[] a, int i, int j) { return a[i-1].compareTo(a[j-1]) < 0; } static void exch(Object[] a, int i, int j) { Object swap = a[i-1]; a[i-1] = a[j-1]; a[j-1] = swap; }

Note there are still N elements in the array, and they are referred to using 1-based indexing. Again, this was done by Sedgewick to make the computations easier to see and understand.

1.3 Ready to explain HeapSort

There are two steps that we complete. First we need to turn an arbitrary array of values into a Heap.

1.3.1 Convert arbitrary array into heap

Consider the following partial array of values. I use "??" to represent any number. If you look at the picture and squint, the numbers that are present could actually already be in their proper spot for all that you know! Or to put it in other words, each of these elements forms a valid heap of 1 element.

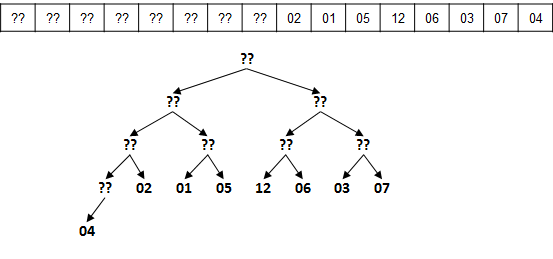
So where is the first element that has a child? If we start counting each element, starting with numbers 1, 2, 3, ... then the position is exactly located at index floor(N/2). See code on (p. 324).

So all we need to do is visit each of the ?? positions in reverse order and call sink on that location to reestablish the Heap ordering property. The code is just a bit more complex because you have to pass in more parameters. First you pass in the array that is being converted into a heap structure; then you pass in N the number of elements, so sink knows when to stop; and you pass in k representing the item location (when counting from 1) to sink:

static void sink(Comparable[] a, int k, int N) { while (2*k <= N) { int j = 2*k; if (j < N && less(a, j, j+1)) j++; if (!less(a, k, j)) break; exch(a, k, j); k = j; } }

This code should be familiar. Once all floor(N/2) positions have been processed and the array has been turned into a Heap, the sorting process can begin.

1.3.2 Exchange largest into proper place

With just N-1 iterations, it is possible to sort the heap into an array. The largest element is always in the 1st location, so we first swap this with the final element in the heap and decrement the number of elements in the array. This results in an array of N-1 elements and all you need to do is reestablish the Heap Ordered Property starting with the 1st element. Here is what the full sorting code looks like:

public static void sort(Comparable[] a) { int N = a.length; for (int k = N/2; k >= 1; k−−) { // (1) Create Heap from array sink(a, k, N); show(a); } while (N > 1) { exch(a, 1, N−−); // (2) Modify in place, sink(a, 1, N); // exch. max } }

As you review the code above, you can see that the step "(1) Create heap from array" consists of a for loop that executes N/2 times. Each time through, it calls sink, which we have already seen. As you should recall, the worst case performance for sink is directly proportional to log(N). So at first, this loop appears to take (N/2)*(log N). It seems suprising, and can be validated empirically, that the total number of comparisons needed to build the initial heap will be 2N; the intuition behind this result is that it is simply impossible to continually experience the worst case as you work your way (backwards!) calling swim. Hopefully the example will reveal this when you work it out by hand.

We will work through example in class.

1.4 Daily Question

Find the daily question in Canvas to answer.

1.5 Version : 2022/04/14

(c) 2022, George T. Heineman