CS 2223 Apr 12 2022

Lecture Path: 18
Back Next

Expected reading:

Classical selection: Creep by Radiohead, cover Thalia Strings (2015)

Visual Selection:

Musical Selection: Nirvana, Smells Like Teen Spirit (1991)

Visual Selection: Still Life, Severin Rossen (1849)

Live Selection: Creep by Radiohead, cover Thalia Strings (2015)

1 BST recursions and Asymptotic Notation

I am going to finish describing recursive methods within BSTs. We will also more formally present Big O notation and explain it mathematically.

1.1 Computing Floor(key) in BST

This section was introduced on day 15 but I didn’t cover it in class. Doing so now.

Let’s tackle a more challenging question. How about returning the keys in a BST that are closest to a target key, without actually being present in the BST? We use the mathematical concept of Floor and Ceiling as follows:

Floor – find the largest key that is smaller than target
Ceiling – find the smallest key that is larger than target

In a way, you have seen this concept in Binary Array Search. Try the following example by hand:

Search for the value 7 in a sorted array:

+—+—+—+—+—+—+—+—+—+—+—+—+ | 2 | 3 | 5 | 9 | 10| 11| +—+—+—+—+—+—+—+—+—+—+—+—+ 0 1 2 3 4 5 (0) lo mid hi (1) lo mid hi (2) lo mid hi (3) hi lo

When Binary Array Search completes without finding a value, note that the value of lo points to the entry which is the smallest value larger than the target (which makes that the ceiling of 7. To locate the floor, simply look at A[lo-1] to find that element.

Note that the above formulation must be carefully handled when looking for the ceiling of a target greater than any element in the array, or for the floor of a target smaller than any element in the array.

What changes when we try to have a Binary Search Tree support the floor (or ceiling) method?

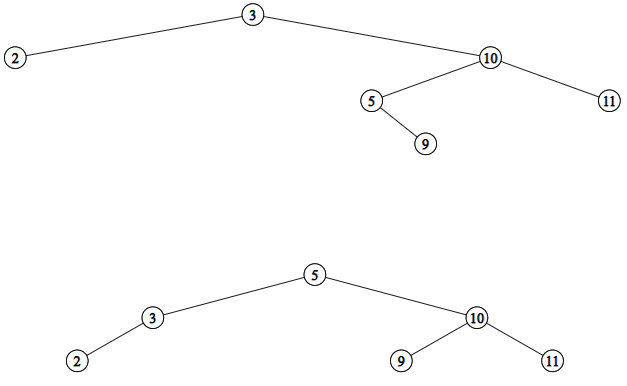
Given this definition of Floor, let’s review the code.

public Key floor(Key key) { Node rc = floor(root, key); if (rc == null) return null; return rc.key; } private Node floor(Node parent, Key key) { if (parent == null) return null; int cmp = key.compareTo(parent.key); if (cmp == 0) return parent; // Found: this is floor if (cmp < 0) return floor(parent.left, key); // key smaller? try left Node t = floor(parent.right, key); // greater? parent might if (t != null) return t; // be floor, but only if return parent; // no other candidate }

1.2 Discussion of Sorting Algorithms

For the homework you are to empirically determine the most number of times that exch is called when using five different sorting algorithms on problems of size N.

ExchangeableVisualizer

Discuss in class.

1.3 Asymptotic Analysis

What if we go back to HW2 and run Analysis to determine the growth of the value printed out.

Consider the notes.xlsx file in Canvas.

You can find a wealth of information on Algorithms on the Internet. This Khan Academy Algorithms presentation is of higher quality:

In particular, you can start with

1.4 Big O Notation Cheat Sheet

Big O Cheat Sheet contains a summary of the information for various algorithms and data structures we have seen so far.

1.5 Daily Question

Find the daily question in Canvas to answer.