CS 2223 Apr 26 2021

Lecture Path: 19
Back Next

Musical Selection: UB40: Can’t Help Falling In Love (1993)

Visual Selection: The Starry Night, Vincent Van Gogh (1889)

Live Selection: White Rabbit, Jefferson Airplane, 1969

1 Graphs and Next Steps

1.1 Graphs

We are now studying a new domain in computer science called Graphs. A graph represents not just a set of items but the relationships between those items, which may be dynamically changed.

Figure 1:

Figure 2:

It is truly interesting to study graphs because there are several possible structures you can use to implement graphs, and there is no standardized solution that everyone agrees with.

Figure 3:

Start with some definitions:

A graph is a set of vertices and a collection of edges that each connect a pair of vertices.

Note that the graph is defined by a set of vertices; each vertex is therefore unique. Each vertex may have any number of edges (zero or more). However, it is common to avoid the following situations:

• Self-loops: when a vertex has edge back to itself

• parallel edges: when a vertex has multiple edges to the same paired vertex.

For our purposes, we will focus on simple graphs that avoid these two anomalies.

In this first lecture we are going to cover a number of new terms that are necessary to understand within the domain of graphs.

• Vertex u is adjacent to vertex v if there exists an edge (u,v) in the graph.

• A subgraph is a subset of a graph’s edges and the vertices that are connected to those edges.

• A path is a sequence of vertices connected by edges.

• A cycle is a path with at least one edge whose first and last vertices are the same.

• The length of a path or a cycle is the number of edges in the path.

• A graph is connected if there is a path from every vertex to every other vertex in the graph.

1.2 Trees

We have covered the Binary Tree structure in the context of Binary Search Trees, but when we come to graphs, the term Tree is a more generalized term.

A Tree is a graph that is fully connected and contains no cycles.

1.3 Structural Concerns

The vertices in a graph are essentially abstract concepts. For convenience, then, we simply refer to each vertex by 0, 1, ..., V-1 for a graph with V vertices.

For the algorithms we cover, we do not address situations where a vertex is added or removed; adding this capability doesn’t really change the complexity of the algorithms.

Naturally it becomes more convenient to have "names" or other arbitrary data associated with each vertex. To make this work, we will use the following standard:

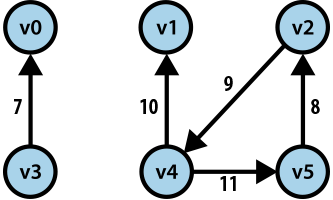
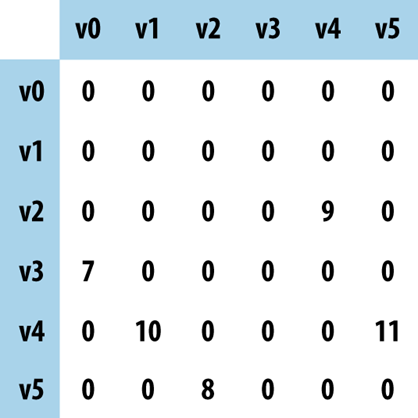
SeparateChainingHashST<String,Integer> map = new SeparateChainingHashST<>(); SeparateChainingHashST<Integer,String> reverse = new SeparateChainingHashST<>();

map takes an arbitrary string and returns its associated vertex number (0, 1, ..., V-1) while reverse takes a given vertex number and returns its associated string. With these structures, we can retrieve (in ~ constant time) the necessary information for a vertex.

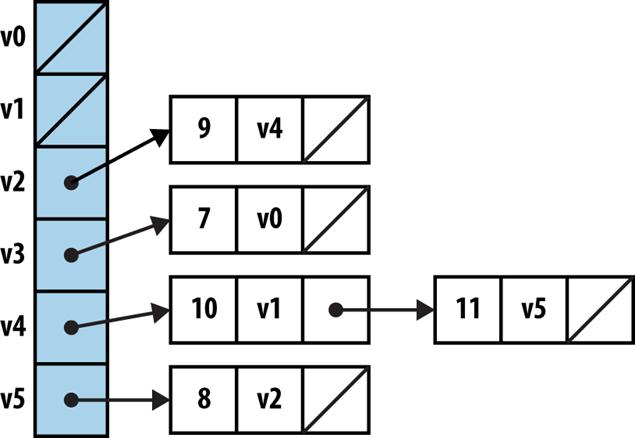
We can store a graph using any of the data structures we have seen so far. Two possibilities immediately come to mind:

Figure 4: Adjacency Matrix

Figure 5: Adjacency List

Which of these solutions is "best"? Well, it depends on the nature of the information you are storing

In 2012, Airports Council International (ACI) reported a total of 1,598 airports worldwide in 159 countries, resulting in a two-dimensional matrix with 2,553,604 entries. How many of these entries has a value? Well, that depends on the number of direct flights. ACI reported 79 million "aircraft movements" in 2012, roughly translating to a daily average of 215,887 flights. Even if all of these flights represented an actual direct flight between two unique airports (clearly the number of direct flights will be much smaller), this means the matrix is 92% empty. This is a good example of a sparse graph.

A complete graph is one where there is an edge between a vertex and every other vertex in the graph.

Since there could be on the order of V*(V+1)/2 possible edges in a graph with V vertices, then in a dense graph, the number of edges is proportional to the square of the number of vertices. In a sparse graph, the number of edges is proportional to the number of vertices.

1.4 Mathematical Analysis

When analyzing graphs and graph algorithms, we will typically use two variables in our formulae:

• V – The number of Vertices

• E – The number of Edges

And often the performance of a specific algorithm will improve (or degrade) based on whether a graph is sparse or dense.

1.5 Processing Graph Queries

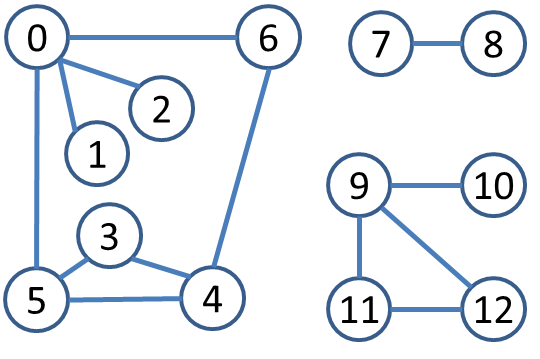
Let’s get started with a simple request. Given the above graph, can you find all Triangles that exist, namely, three vertices u, v and w in which all three edges (u,v), (v,w) and (u,w) exist and these vertices are all different.

Let’s brainstorm for a bit. How would you imagine doing this? How would you make sure that you don’t double count the number of triangles that you see?

Sample code FindTriangle contains different variations on this problem. The basic premise looks like this:

for (int u = 0; u < g.V(); u++) { // for all vertices u... for (Integer v : g.adj(u)) { // find a neighbor v to u for (Integer w : g.adj(v)) { // then find neighbor w to v for (Integer x : g.adj(u)) { // and check if w is neighbor to u if (x == w) { // Triangle } } } } }

The above will overcount the number of triangles and so you need to divide the toal number found by 6, since there are 3! permutations of each of the vertices.

This triangle finding example is rather specific and we likely need some more generic searching capability. This week we cover a number of graph searching algorithms to address this very question.

This is going to take awhile! N E Count Est. 8 13 5 7.0 16 65 84 70.0 32 253 624 620.0 64 1009 5145 5208.0 128 4060 42414 42672.0 256 16334 174082 345440.0 512 65435 692346 2779840.0

1.6 Version : 2021/04/27

(c) 2021, George T. Heineman