CS 2223 Apr 27 2021

Lecture Path: 20
Back Next

Musical Selection: My Shot, Lin-Manuel Miranda et al. (2015)

Visual Selection: Diogenes Sitting in his Tub, Jean-Leon Gerome (1860)

Visual Selection: Twist and Shout, The Beatles, 1964

1 Working With Graphs

I hope you’ve had the chance to read up on the Graph concept from yesterday’s lecture.

As we will see, you can implement a wide variety of algorithms simply by working with this Graph API. Now there are two proposed strategies for storing graphs.

• Adjacency Matrix – Use a V-by-V boolean two dimensional array where entry [v][w] determines whether there is an edge from v to w. Space is prohibitive and would be useful only for very dense graphs.

• Array of Adjacency Lists – Use a one-dimensional vector of size V to record the collection of edges that are adjacent to each vertex. In an undirected graph, each edge appears twice.

We will work in lecture using the Adjacency Lists implementation and you will get a chance to see the Adjacency Matrix implementation on a homework assignment.

As summarized on page 527, the order of growth performance for each of the graph implementations is as follows:

Adjacency matrices have excessive space costs and unexpectedly high cost to iterate over neighbors of v.

1.1 Constructing Graphs

It is not as convenient to work with graphs because it takes so long to set them up "from scratch". It is common to store information in a file and load it up to instantiate the graph. On page 529 of the book there is an example file tinyG.txt which contains the following:

13 13 0 5 4 3 0 1 9 12 6 4 5 4 0 2 11 12 9 10 0 6 7 8 9 11 5 3

I created a class, GraphLoader to easily load up a graph file from disk. The format is Sedgewick’s own.

The first line shows the number of nodes (in this case 13). The second line shows the number of edges (oddly enough, 13 again). Then the next 13 lines all contain a single edge described by two integers representing the vertices in the graph.

When a Graph is constructed from this file, the following is the result.

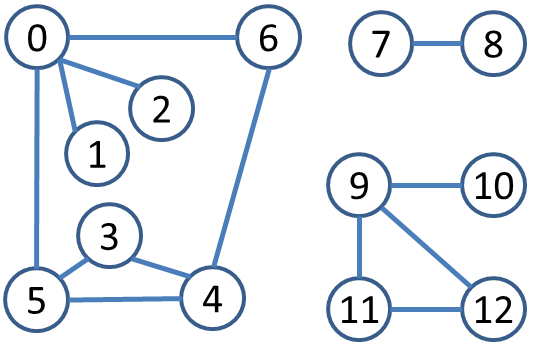
The following shows the adjacency matrix representation for this graph.

00 01 02 03 04 05 06 07 08 09 10 11 12 00 1 1 1 1 01 1 02 1 03 1 1 04 1 1 1 05 1 1 1 06 1 1 07 1 08 1 09 1 1 1 10 1 11 1 1 12 1 1

1.2 Processing Graph Queries

There are a number of common queries that you would have given a graph structure. The most common is based on reachability, namely, can you start at a given vertex v and find a path to another vertex w. And you must perform this computation as efficiently as possible.

1.3 Search Graphs

To motivate searching over graphs, consider the following maze:

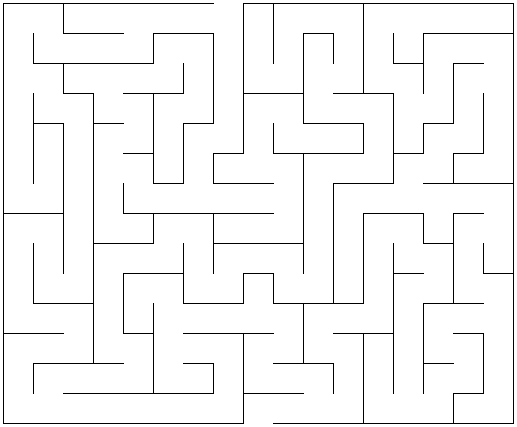
Think about how you solve this maze. For the purpose of this course, let’s represent the maze as a graph. I only show a fragment of this construction:

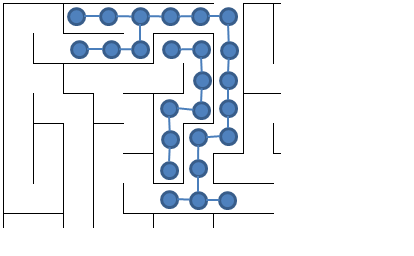
In computer science we routinely transform problems; in this case, we are going to solve a maze by transforming it into a graph of NxM vertices (one for every positions in the N rows and M columns. An edge in the graph exists if two positions are neighbors with no wall between them. This is an example of a sparse graph.

1.4 Initial Approach to Searching a Graph

Let’s use some intuition to construct our first algorithm for searching through a graph. If only we had some way to keep track of our progress! Let’s imagine marking nodes that we have already seen.

public DepthFirstSearch (Graph g, int s) { marked = new boolean[g.V()]; this.g = g; dfs(s); } /** Continue DFS search over graph by visiting vertex v. */ void dfs (int v) { marked[v] = true; // we have now seen this vertex count++; // look into neighbors for (int w : g.adj(v)) { if (!marked[w]) { // will never dfs() on this vertex again dfs (w); } } }

This proceeds until all vertices reachable from the initial vertex s have been processed.

Now, in what order are the vertices processed? It depends on the way they are traversed with the for (int w: g.adj(v)) code. And the order unfortunately depends upon the way that the adjacency list stores the neighbors.

Since we are using a Bag to store the vertices, we have no way to know what this ordering will be. But does it really matter? Since this is a blind search the answer is no!

However, when we work on examples in class or perhaps on an exam, I will always assume that neighboring vertices are iterated in ascending order based upon their unique identifier.

1.5 Demonstrate DepthFirstSearch

Demonstrate using Shell and running DepthFirstSearch on the files tinyG.txt and tinyCG.txt.

There are several observations to make:

• The number of invocations of dfs will also be ≤ V.

• Each edge (u,v) is visited twice, once as a neighbor of u, and once as a neighbor of v.

• The Depth of the recursion ≤ V.

1.6 Recovering Path

This small search utility demonstrates the behavior of Depth First Search, but it doesn’t really do much. Let’s add behavior to recover the path from a designated vertex, s, to any vertex that is reachable from s over the existing edges in a graph.

At first it seems we have to keep track of a lot of information, because there are so many directions in which the search might go. However, instead of thinking about the starting point of an arrow, focus on the ending point of the arrow.

The counter-intuitive solution to this problem is to record a separate one-dimensional vector for each vertex that records the previous vertex in a depth first search from the original s source vertex.

1.7 Sample Exam Question

You are given the following graph. Assuming that all adjacency lists are ordered by increasing vertex number, conduct a depth first search of the graph starting at vertex 0 and stopping when you reach vertex 7.

Show your progress by coloring completed vertices in Black while marking in-progress vertices with an X.

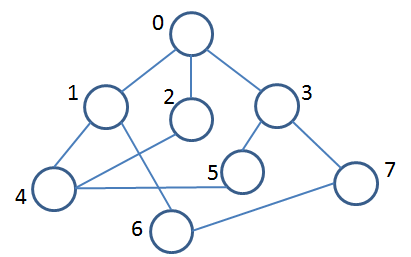
Find fully worked out step-by-step answer in Canvas under Files | in-class exercises | day20_DFS_StepByStep

1.8 Daily Question

What happens to Depth First Search if the graph is not connected?

1.9 Version : 2021/04/27

(c) 2021, George T. Heineman