CS 2223 Apr 01 2021

Lecture Path: 06
Back Next

1 Sorting Principles

As a general comment, you will likely only implement a data type or data structure "from scratch" within an academic context, such as this course. My focus is to make sure that you can understand code examples and pseudocode.

1.1 Important concepts from readings

• Sorting processes arrays of items where each item contains a key.

• Mathematically determine how many comparisons.

• Mathematically determine how many exchanges (or swaps).

• Fully ordered Items, also Reflexive, Antisymmetric, and Transitive.

• CompareTo Interface

1.2 Opening Questions

Did anyone solve daily exercise for splitting a Bag in half?

1.3 Thoughts on Tilde Approximation

This dicussion relates back to page 181 of the book. The purpose of this notation is to try to estimate the total number of key operations, which will directly lead to an understanding of the overall performance of the algorithm.

Figure 1: Anatomy of execution (p.181)

This analysis derives the following cost model:

Figure 2: Cost Model (p.181)

The Tilde Approximaion is an invention of Sedgewick. While it may be useful in the beginning, in the long run, it will not be satisfactory when tackling more interesting problems.

That said, the tilde approximations can be useful for identifying the "Order of Growth" in a mathematical way that helps support the empirical evidence that may strongly suggest an algorithm’s behavior.

And this leads into a discussion on the Big O notation. I am going to introduce its usage NOW, and then provide the full formalized proofs for this notation later in the course.

The "O" in Big O stands for "Order of growth" and is used by algorithm designers to evaluate the performance of an algorithm independent of the programming language used to implement it. This notation, developed in the 1970s, is (in my mind) inspired by Moore’s Law, which takes as its premise that the speed of computer CPUs doubles every eighteen months. In other words, there is no point in predicting how fast an algorithm will run, since you just have to wait a year and it will magically run faster. However, once you run the same algorithm on the same computer on problems of different size then you can predict the runtime performance based on your knowledge of the algorithm.

We will start by empirically observing runtime performance (or counts of how many times a key operation executes) and use this data to build a model for performance. Over time, I will enhance and more formally define the Big notation.

I start with the probing question: What happens to the performance of an algorithm as it processes problem instances that have doubled in size?

How large will count be after running this code?

int count = 0; for (int i = 0; i < N; i++) { for (int j = 0; j < N; j++) { count++; } }

Now as N doubles in size, what happens to count? That’s right – it is FOUR times as big. I also want to make the connection that the magnitude of count is a proxy for the runtime performance on a computer of your choosing. I only have to adjust the scale based on the specific nature of the computing device. One more expensive computer could be 100 times faster than another computer. This is known as a multiplicative constant.

If an algorithm your computer solving the above takes 5 minutes for a given N, it will take 20 minutes if the problem size doubles. Now, you can move over to that more expensive computer to run the code in about 12 seconds. However - even on that computer, subsequent doublings of the problem size will result in execution times that are four times longer.

What if I make the following change...

int count = 0; for (int i = 0; i < N; i++) { for (int j = i+1; j < N; j++) { count++; } }

Figure 3:

1.4 Sorting Groundrules

The best way to compare sorting algorithms is to develop a benchmark approach to properly compare "apples to apples." Sedgewick does this by defining two fundamental operations:

• boolean less (Comparable v, Comparable w) – This determines whether v is strictly smaller than w. It may seem odd, but you can do sorting without actually ever checking whether two objects are equal.

• void exch (Comparable[] a, int i, int j) – Exchanges the elements within the array at positions i and j.

In this regard, we are approaching sorting as Computer Scientists where we can set up experiments and identify valid sorting algorithms and compare their behavior with one another.

Another feature of the Sedgewick approach is to demonstrate the sorting algorithm on small data sets. This allows you to understand the mechanics fully so you can then empirically validate its performance against the predicted speed.

In most cases it doesn’t matter what type of object is being sorted. However it is worth noting that more complicated objects will have slowed performance when computing the less operator between two items.

The goal of these next few lectures – and indeed the entire chapter on Sorting – is to demonstrate a range of mathematical analytic skills to predicting the performance of different algorithmic approaches towards a common problem.

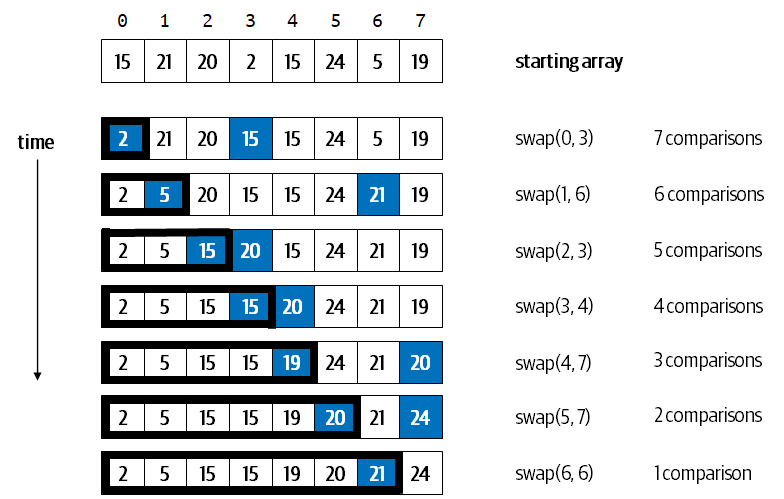
1.5 Selection Sort

This approach is a very "human-centered" approach to sorting, one which you might already employ on a daily basis.

Since the goal is to sort the entire array, selection sort starts by locating the smallest element in the array and swapping it with the a[0]. As you already know, this will take n-1 less comparisons. Once this step is completed, you now have a problem that has decreased in size by 1, namely, you want to sort the "right-side" of the array, which is one size smaller.

If you continue this logic, in n-2 less comparisons, you can find the element that is to be switched with position a[1].

public static void sort(Comparable[] a) { int N = a.length; Truth_____________________________ for (int i = 0; i < N; i++) { int min = i; Truth___________________________ for (int j = i+1; j < N; j++) { if (less(a[j], a[min])) { min = j; } } Truth___________________________ exch(a, i, min); Truth___________________________ } Truth_____________________________ }

Describe and explain expected time performance

Figure 4:

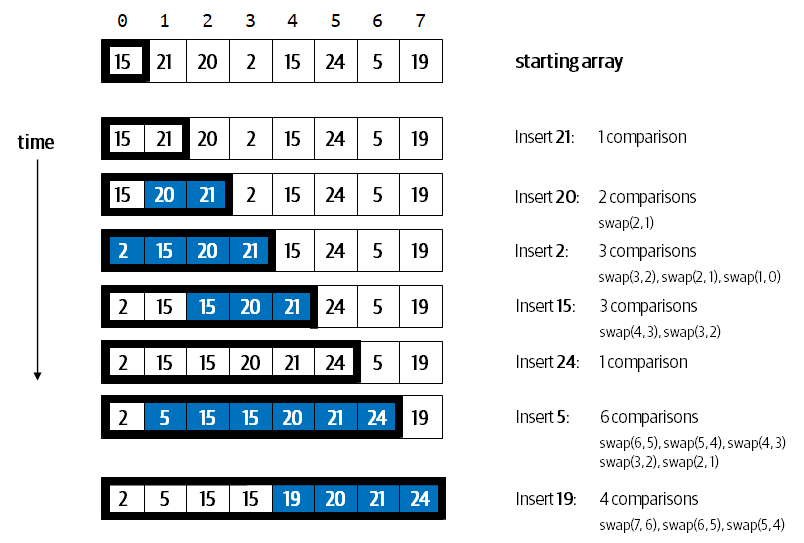
1.6 Insertion Sort

Insertion sort is nominally better because it chooses a different strategy for sorting. It first observes that the a[0], when considered by itself, is already sorted. What about the a[1]? If it is already in position (i.e., it is greater than a[0]) then nothing needs to be done, otherwise they are swapped.

If you continue this logic, you might be able to see that the goal of this method is to assume that a[0] .. a[i] are already sorted, and then it tries to see where a[i+1] should be inserted into place. It performs this task from the right down to the left, that is, in decreasing order, because it may be that a[i+1] is already in position by being greater than a[i]. When this is not the case, the algorithm exchanges neighbors while trying to locate the proper place to insert a[i+1]. Once done, the array a[0] .. a[i+1] is sorted.

This algorithm also reduces the size of the problem to solve by one, but it has some nice attributes that are worth hilighting:

• It is the only sorting algorithm we will present which benefits when items are already in sorted order.

• There are more exchanges in Insertion Sort than Selection Sort.

Describe and explain expected time performance

public static void sort(Comparable[] a) { int N = a.length; Truth_____________________________ for (int i = 0; i < N; i++) { for (int j = i; j > 0 && less(a[j], a[j-1]); j−−) { exch(a, j, j-1); } Truth_____________________________ } Truth_____________________________ }

Figure 5:

1.7 Sample Exam Question

This one relates to linked lists as seen with the Bag data type. How would you implement a contains method that determines whether an element is to be found in tbe Bag.

/** @param <Item> the type of elements in the Bag */ public class Bag<Item> { Node first; // first node in the list (may be null) class Node { Item item; Node next; } /** Determine whether item is contained in the bag. */ public boolean contains (Item item) { // fill in here... } }

Also evaluate the performance of the method in terms of N, where N is the number of elements in the Bag.

1.8 Daily Question

The assigned daily question is DAY06 (Problem Set DAY06

If you have any trouble accessing this question, please let me know immediately on Discord.

1.9 Version : 2021/04/01

(c) 2021, George T. Heineman