CS 2223 Mar 30 2021
Daily Exercise: Digits summing to 100
Sample Exam Question: Swap bottom two elements on stack
Classical selection:
Beethoven Symphony No. 1 (1800)
Musical Selection:
She Believes In Me, Kenny Rogers (1979)
Visual Selection:
Reptiles, M.C. Escher (1943)
Live Selection:
Rhapsody in Blue,
George Gerwshin (1924), Leonard Bernstein (1976)
Daily Question: DAY05 (Problem Set Day05)
1 A Journey of a thousand miles begins with a single step
1.1 Survey Results
1.2 Important concepts from readings
Goals are the links in the chain that connect activity to accomplishment
Tom Ziglar
A linked list is a recursive data structure that is either null or a reference to a node that stores some item and has a reference to a linked list
A Bag can be readily implemented from linked list
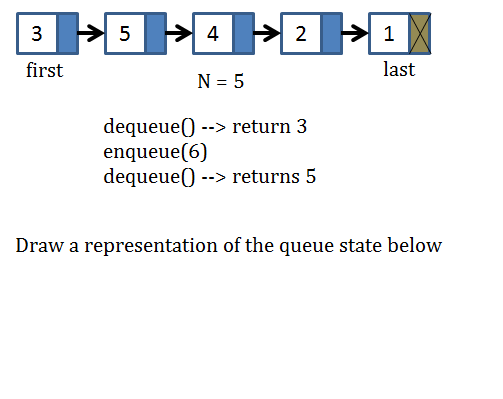
Maintain two pointers (first and last) to properly implement Queue data type
1.3 Opening Questions
Review the lecture challenge My Solution
1.4 Solve sample Stack Exam problem
Here is pseudocode that would be suitable for an exam solution
function swapBottomTwo (Stack s) { if size of s < 2 return Stack backup = new Stack while s is not empty backup.push(s.pop()) oldest = backup.pop() next = backup.pop() s.push(next) s.push(oldest) while backup is not empty s.push(backup.pop() }
Bonus question
1.5 Fixed Capacity Queue Implementation
Ok, this is a bit of a straw-man presentation. The point is that it is possible to implement Queues using a fixed capacity, as we did with Stacks, although the performance is not what you would want.
public class FixedCapacityQueue<Item> { private Item [] a; // holds the items private int N; // number of items in queue // create an empty queue with given capacity public FixedCapacityQueue(int capacity) { a = (Item[]) new Object[capacity]; N = 0; } public boolean isEmpty() { return N == 0; } public boolean isFull() { return N == a.length; } public void enqueue(Item item) { a[N++] = item; } public Item dequeue() { Item val = a[0]; for (int i = 0; i < N; i++) { // shift all elements down one a[i] = a[i+1]; } a[−−N] = null; // clear unused and reset size return val; // value that was dequeued } }
What is the performance of the operations of this data type? Do you see opportunities for improvement?
1.6 Fixed Capacity Circular Queue Implementation
You need to be aware of an alternate implementation of a fixed capacity queue that works very well in practice, and is easy to embed in hardware devices. Yes, we cannot always assume that we have infinite storage or storage that can be dynamically allocated.
The basic concept is a circular buffer. Instead of moving the elements in the queue around, we update two index values, first and last. When the queue is not full, last tells you the index location into which an element will be enqueued. When the queue is not empty, first tells you the location of the element to be dequeued. When enqueing a value (or dequeing a value), you need to increment last (or first, respectively). Code is available in the repository. To simplify computation, keep an extra variable, N, to count the number of elements in the queue. There are ways to avoid having to keep an extra value, but they either make the code too complicated or waste one of the spaces in the array.
public class CircularBufferQueue<Item> { private Item[] a; // holds the items private int N; // number of items in queue private int first; // start of the queue private int last; // end of the queue // create an empty queue with given capacity public CircularBufferQueue(int capacity) { a = (Item[]) new Object[capacity]; N = 0; } public boolean isEmpty() { return N == 0; } public boolean isFull() { return N == a.length; } public void enqueue(Item item) { if (isFull()) { throw new IllegalStateException("Queue is Full."); } a[last] = item; N++; last = (last + 1) % a.length; } public Item dequeue() { if (isEmpty()) { throw new IllegalStateException("Queue is Empty."); } Item val = a[first]; N−−; first = (first + 1) % a.length; return val; } }
This code makes use of the modulo (%) operator, which returns the remainder of a number when divided by a given integer. Doing so allows you to easily move to the "next" position and have that wrap around as necessary.
The following small example will help explain the idea:
Note that in this example, you can say that:
"when the queue is non-empty, first is the index position of the first item in the queue"
and
"When the queue is non-empty, last is the index position immediately after the last item in the queue (wrapping around to 0 as necessary)."
Try this for a programming exercise
1.7 What is a Linked List?
A linked list is a recursive data structure that is either null or a reference to a node that stores some item and has a reference to a linked list (p. 142). This is the fundamental data structure used historically for dynamic storage. In this class we are often shielded from this low-level data structure, but it is critical that you know how to work and manipulate linked lists.
1.8 Linked List offers the perfect data structure for Bag
Operation | Bag | Queue | Stack |
add | add(Item) | enqueue(Item) | push(Item) |
remove | -- | dequeue() | pop() |
size | size() | size() | size() |
isEmpty | isEmpty() | isEmpty() | isEmpty() |
We only want to offer three operations. The following class makes use of Java Generics to construct a Bag of Item objects.
public class Bag<Item> { Node first; // first node in the list (may be null) class Node { Item item; Node next; } public void add (Item item) { Node oldfirst = first; first = new Node(); first.item = item; first.next = oldfirst; } }
As you can see from the depiction of linked objects in the book, you can use these structures to represent dynamically growing linear lists of objects.
Page 155 of the book completes the Bag implementation, with the ability to iterate over all of the elements in the Bag. Review and ask questions as needed.
1.9 Linked List Queue Implementation Resolves Resizing
Page 151 describes how to provide constant time performance for enqueue and dequeue operations. This is done using Linked Lists to structure the information.
public class Queue<Item> { private Node<Item> first; // beginning of queue private Node<Item> last; // end of queue private int N; // number of elements on queue // helper linked list class class Node<Item> { private Item item; private Node<Item> next; } public Queue() { first = null; last = null; N = 0; } public boolean isEmpty() { return first == null; } public int size() { return N; } /** Adds the item to this queue. */ public void enqueue(Item item) { Node<Item> oldlast = last; last = new Node<Item>(); last.item = item; last.next = null; if (isEmpty()) { first = last; } else { oldlast.next = last; } N++; } }
We need to go over the implementation, but the concepts should be clear from the earlier presentation of Circular Buffer.
Under what circumstances is the first reference updated during enqueue?
Under what circumstances is the last reference updated during enqueue?
Once enqueue is considered, you need to also have dequeue method:
public Item dequeue() { if (isEmpty()) throw new NoSuchElementException("Queue underflow"); Item item = first.item; first = first.next; N−−; if (isEmpty()) last = null; // to avoid loitering return item; }
Under what circumstances is the last reference updated during dequeue?
1.10 Stack Resizing Logic
What happens when you more-than-double upon resizing? What about the shrink factor?
The problem is complicated because it is hard to come up with the "average case" for a stack. How do you balance the number of pushes versus the number of pops? They can’t be drawn from the same random distribution, because if they did, then the stack wouldn’t grow enough to warrant being resized. Somehow you need to generate behavior with "spikes" to force the resize, followed by lots of needless operations that do not affect the size, followed by a sudden removal of a number of elements via pop.
1.11 Lecture Takeaways
Be sure to review Rubric for homework HW1
Need practice in pointer/reference manipulation
1.12 Daily Exercise
See if you can do this one. You are given a reference to the first node in a linked list, L, that contains N elements. You are to only traverse the linked list ONCE. The result is to split L into two lists, L and back, where L is updated to only contain the first floor(N/2) elements (in their original order) and back contains the remaining N - floor(N/2) elements (in their original order).
To be more precise, do this operation within the context of Bag
public class Bag<Item> { /** This operation will return a new Bag that contains the remaining N - floor(N/2) elements while modifying the current bag to retain only the first floor(N/2) elements. */ public Bag cutInHalf() { } }
1.13 Daily Question
The assigned daily question is DAY05 (Problem Set DAY05)
If you have any trouble accessing this question, please let me know immediately on Discord.
1.14 Version : 2021/03/30
(c) 2021, George T. Heineman