CS 2223 Apr 02 2021

Lecture Path: 07
Back Next

Musical Selection: Rick Springfield: Jessie’s Girl (1981)
Visual Selection: Primavera, Sandro Botticelli (1470s-1480s)
Live Selection:Take me to the pilot (1971), Elton John (1998)
Daily Question: DAY07 (Problem Set DAY07)

1 Mergers and Acquisitions

Selection Sort and Insertion Sort both operate in linear fashion. That is, they each seek to reduce the size of the problem by one with each iteration.

Can we find someway to divide the problem in half with each pass? MergeSort offers the ability to do just this.

1.1 Sorting a linked list

Yesterday in class I raised the possibility of sorting a linked list of values. I went ahead and did this. Find the solution in LinkedListSort. I wondered whether Selection Sort or Insertion Sort would provide inspiration – it turns out that Selection Sort is more helpful. If the linked lists were doubly-linked (where each node also linked to its previous node) then it is likely that Insertion Sort would provide some guidance.

1.2 Preface Materials

Hmm, difficult. VERY difficult. Plenty of courage, I see. Not a bad mind, either. There’s talent, oh yes. And a thirst to prove yourself. But where to put you?
The Sorting Hat
Harry Potter and the Philospher’s Stone

But first, last year’s midterm has been posted in Canvas (see announcement to this effect). Note that you will see a question that asks for an extensive Tilde analysis of an algorithm. As I have said in class, I will no longer be focusing so intently on Tilde analysis, so that kind of question (Question #2) will not be on this year’s midterm exam.

1.3 Merge Sort

Unfortunately, the first attempt at doing so typically leads to excessive wasted storage that slows everything down. Let’s show what the code would look like (find it in the repository as AnnotatedWastedSpaceMerge}.

public static void sort(Comparable[] a) { sort (a, 0, a.length-1); } static void sort (Comparable[] a, int lo, int hi) { if (hi <= lo) return; int mid = lo + (hi - lo)/2; sort(a, lo, mid); // recursively sort a[lo..mid] sort(a, mid+1, hi); // recursively sort a[mid+1..hi] merge(a, lo, mid, hi); // merge two together }

This is surprisingly succinct. To see the overall behavior, review AnnotatedWastedSpaceMerge} which shows the behavior when sorting an array of eight elements, a[0..7]:

sort(0,7) 1. sort(0,3) 1. 1. sort(0,1) 1. 1. 1. sort(0,0) 1. 1. 2. sort(1,1) 1. 1. 3. merge(0,1) 1. 2. sort(2,3) 1. 2. 1. sort(2,2) 1. 2. 2. sort(3,3) 1. 2. 3. merge(2,3) 1. 3. merge(0,3) 2. sort(4,7) 2. 1. sort(4,5) 2. 1. 1. sort(4,4) 2. 1. 2. sort(5,5) 2. 1. 3. merge(4,5) 2. 2. sort(6,7) 2. 2. 1. sort(6,6) 2. 2. 2. sort(7,7) 2. 2. 3. merge(6,7) 2. 3. merge(4,7) 3. merge(0,7)

The reason Mergesort works in the "real world" is that there is no need to worry about extra storage; as long as you have "room" on the table, then you will have place to put the merged results. But we don’t have that luxury in software. One option (which leads to wasteful space) is shown below.

To understand how the merge function works, recognize that it starts with a single array, a, that is sorted in ascending order from a[lo..mid]; in addition, a[mid+1..high] is also sorted in ascending order. This inefficient solution smakes a full copy of a[lo..hi] into aux (first for loop).

It then (in the second for loop) completes the merge. To see the "wasteful" memoray usage of this implementation, consider the output when sorting a number of sample arrays:

N Extra Estimate = 2*N*log N - 2*N 4 8 8.00 8 32 32.00 16 96 96.00 32 256 256.00 64 640 640.00 128 1536 1536.00 256 3584 3584.00 512 8192 8192.00

As you can see from the above table, if you allocate extra storage within merge, you quickly realize that you are simply wasting space. Fortunately, the fix is an easy one to make (p. 273). Instead of allocating the storage within each sort invocation, do so once when the function begins.

We are now ready to talk about the "in-place" merge sort.

So we need to explain how merge works with an auxiliary array, which is accessible to the merge function:

The key is the final for loop. While it looks complicated at first, you can break it down into four cases as follows, which matches the above code

• (left > mid) Have you exhausted left elements?

• (right > hi) Have you exhausted right elements?

• (less(aux[right]], aux[left]) Take element from right if smaller

• Else we take element from left because it is larger or equal

1.4 Recursive in-class demonstration

Work through example on small array (from p. 273)

E M R G E S O R

Review in debugger in Eclipse (AnnotatedMerge)

1.5 Comparison analysis

Mergesort uses between ~1/2 N log N and N log N comparisons to sort any array of length N (p. 272).

How can we show this? Let’s develop a mathematical model that counts the number of comparisons, C(n), for sorting n elements. For starters, let’s assume that n is a power of 2. This simplifies the accounting of operations, and in the long run, this won’t affect the results since we will be able to show that the result holds even for n that are not powers of two.

First focus on the number of comparisons in merge (a, lo, mid, hi). Consider when a[lo..mid] has two elements and so does a[mid+1..hi]. With each comparison you advance either i or j, and it is possible that this could happen just 3 times, before one of them fall off the range. Check this out yourself:

i: [ 2, 4 ] merge j: [ 1, 3]

is 1 < 2? Yes, so advance j
is 3 < 2? No, so advance i
is 3 < 4? Yes, so advance j

To generalize, you could go as far as N-1 comparisons where N is the sum of the lengths of the two arrays being merged.

In the best case, you would only compare N/2 elements since one would become exhausted.

So you can’t do FEWER than N/2 and you can’t do more than N-1.

To clean this up, we’ll just say:

So you can’t do FEWER than N/2 and you can’t do more than N.

So now ready for the big claim:

C(N) <= C(N/2) + C(N/2) + N
C(N) >= C(N/2) + C(N/2) + N/2

This is a very accurate evaluation. To compute the upper bound for C(N) we use the first equation above and try to find equality:

Now we assume N is a power of 2, or 2n. Thus we have

C(2n) = 2*C(2n-1) + 2n.

If you recursively replace the right-most C(2n-1) you get:

C(2n) = 2*[2*C(2n-2) + 2n-1] + 2n.

Let’s do one more time to see the effect:

C(2n) = 2*[2*[2*C(2n-3) + 2n-2] + 2n-1] + 2n.

If you expand out the multiplications, you get the following:

C(2n) = 8*C(2n-3) + 2n + 2n + 2n.

As you look at this equation, it looks like the following:

C(2n) = 2k*C(2n-k) + k*2n.

Now replace back:

C(N) = 2k*C(2n-k) + k*N

So the final question to ask is how many times can you increase k? The answer is log(N), at which point C(1) means no comparisons for a single element. Thus the final equation we develop is:

C(N) = N * log N as an upper bound on the number of comparisons.

The analysis becomes more complicated when N is not a power of 2, but this suffices for lecture. Thus C(N) is ~N log N.

1.6 Array access analysis

Mergesort uses at most 6N log N array accesses. This works out in similar fashion and I won’t do it here (please see p. 275).

1.7 Final information for HW1

Question 4 on the homework asks you to investiage the performance of the various quantum search algorithms. How can you do this since you do not have access to my code? Well, the provided table contains the list of total probes that were needed to complete a given number of probes on a problem of size N.

How many probes? Well, for each question it is different (and I’ve just updated the HW1 homework description).

• Slicer – N*N targets searched for

• Manhattan Square – N*N targets searched for

• Heisenberg – 10*N+1 targets searched for

• FuzzyFinder – 10*N*N + 1 targets searched for

In each trial, a given number of targets are searched within a problem of size N. Starting from this table, normalize each entry so it represents the average number of probes per target.

With this information in hand, your goal is to try to detect the trends in this data set based on What happens to this average number as the size of the problem instance doubles from N to 2N. There are some distinct possible results:

• O(1) – The results appear to be constant and unchanging. Or, based on small variations in the problem size, they could also slightly decrease

• O(log N) – As the problem size doubles, the average number increases by a fixed amount. Think about Binary Array Search, where the while loop in the algorithm executes just one more time when faced with an array that is twice as big.

• O(N) – As the problem size doubles, the average number also doubles, more-or-less.

• O(N log N) – This is hard to quantify because there are so few real-world concepts to match this intuition. As the problem size doubles, the average more than doubles, but with a more graceful slope.

• O(N2) – As the problem size doubles, the average number quadruples.

I am asking you to think about the results and do your best shot in assessing the expected performance classification of the different algorithms based solely on the empirical evidence. Once you see the actual code, then these analyses will be firmed up and properly completed.

1.8 Comparison-based Sorting Proposition

So now let’s explain why the Merge Sort analysis interesting.

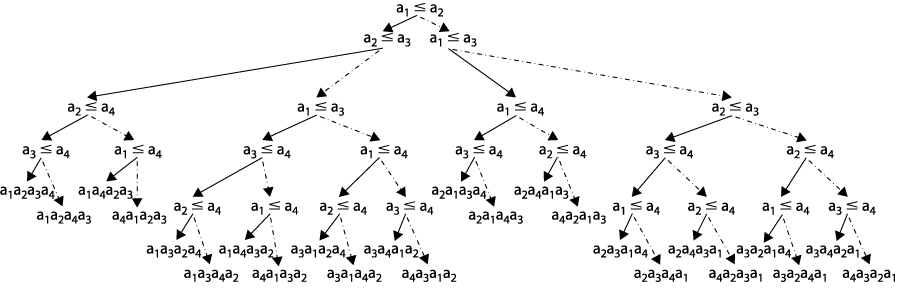
Remember the exercise to compute the fewest number of comparisons needed to sort five elements? If you use comparisons to sort elements, there are some fundamental limits that we can prove. First, consider the following decision tree that reflects the n! permutations of four elements:

Figure 1: Similar to p.281

First verify that all 4!=24 possible permutations exist as leaves in this decision tree. Now the question at hand is the maximum distance from the top decision (a1 <= a2) to any of the permutations.

There are some permutations that only require four comparisons (for example, the leftmost a1a2a3a4. But some require five comparisons, such as in the middle a4a3a1a2. Note that the maximum number of comparisons is 5.

Can we use this observation to make any claim about the maximum height of a decision tree for using comparisons to sort n elements? The answer is yes! First we need to state a properly of binary decisions trees, namely, that a tree with height h has no more than 2h leaves. And in fact, the tree of height h with the maximum number of leaves is perfectly balanced, or complete (see p. 281).

Second observe that the decision tree will have at least n! leaves; after all, you could have an algorithm that reaches the same sorted answer with a different ordering of comparison questions.

Thus N! <= number of leaves <= 2h

Take logarithm of both sides, and you see log(N!) <= h. So all you need is an approximation for log(N!). Try this:

log(N!) = log( N*(N-1)*(N-2)* ... *2*1 )
log(N!) > log( N*(N-1)*(N-2)* ... *N/2) Only go half way
log(N!) > log( (N/2)N/2) Simplify further
log(N!) > (N/2)*log(N/2)
log(N!) > (N/2)*(log N - 1)
log(N!) > (1/2)*N*log N - N/2

Now using Tilde approximation, N*log N will grow more rapidly than N/2, so we can say (finally):

log(N!) is ~ N log N

Because of this confirmation, you know that no sorting algorithm that uses comparisons can guarantee to use fewer than ~ N log N comparisons. This is a lower bound on the difficulty of the sorting problem.

No compare-based sorting algorithm can guarantee to sort N items with fewer than log(N!) comparisons. Note that log(N!) is ~ N log N.

This is a LOWER BOUND on the number of comparisons needed to sort elements.

Mergesort offers an UPPER BOUND on the number of comparisons that it uses.

With this in hand, we can assert the Mergesort is an asymptotically optimal compare-based sorting algorithm.

*whew*

1.9 Interview Challenge

Each Friday I will post a sample interview challenge. During most technical interviews, you will likely be asked to solve a logical problem so the company can see how you think on your feet, and how you defend your answer.

A plane with N seats is ready to allow passengers on board, and it is indeed a full flight; every seat has been purchased. Each person has a boarding pass that identifies the seat to sit in. When the announcement is made to board the plane, all passengers get in line, in some random order.

The first person to board the airplane somehow loses his boarding pass as he enters the plane, so he picks a random seat to sit in.

All other passengers have their boarding passes when they enter the plane. If no one is sitting in their seat, they sit down in their assigned seat. However, if someone is sitting in their seat, they choose a random empty seat to sit in.

My question is this: What is the probability that the last person to take a seat is sitting in their proper seat as identified by their boarding pass?

1.10 Daily Question

The assigned daily question is DAY07 (Problem Set DAY 07)

If you have any trouble accessing this question, please let me know immediately on Discord.

1.11 Version : 2021/04/02

(c) 2021, George T. Heineman