CS 2223 Mar 29 2021

Lecture Path: 04
Back Next

Sample exam question: Postfix processing
Classical selection: Tchaikovsky: Piano Concerto No. 1 (1874)
Musical Selection: Wings: With a little Luck (1978)
Visual Selection: Napoleon Bonaparte, First Consul, crossing the Alps at Great St. Bernard Pass (1803)
Live Selection: La Campabella (Liszt, 1851) (Evgeny Kissin, 2010)
Daily Question: DAY04 (Problem Set DAY04)

1 Arrays are Structures, not types

Did anyone guess why 1255 is such an amazing number?

1.1 Homework 1 Status

I have an anonymous canvas quiz/survey asking you to report on your status of HW1. Please take a few seconds to go there and provide feedback.

Also, I note that in the main loop of ManhattanSquareFinder, I mistakenly only check for (int n=1; n < 10; n++). To validate your ManhattanSquareFinder produces proper results for the 13x13, please change to something like for (int n=1; n < 15; n++).

1.2 Important concepts from readings

• Arrays are a data structure not a type

  We struggle with, agonize over and bluster heroically about the great questions of life when the answers to most of these lie hidden in our attitude toward the thousand minor details of each day.
  Robert Grudin
  Time and the art of living

• If you use array for Stack (or Queue), then you are responsible for managing size dynamically

• Analysis of Experimental data

1.3 Reminder of key operations

The iterators allow you to view the elements of these data types without changing its state.

We have not yet shown how to define an operation that determines whether one of these data types contains a specific value. Use the iterator to retrieve all values without updating its state

public void output (FixedCapacityStackOfStrings stack) { for (String s : stack) { StdOut.println(s); } }

1.4 Answer to question from yesterday

Yesterday I asked the following question:

You are given a train track arrangement with an incoming track containing (from left to right) cars 1, 2, 3, ..., N. There is a single spur that can contain up to N cars, and a single outgoing track. What are the most number of permutations that you can achieve on the outgoing track. There are a total of N! total possibilities.

Answers

Check out the implementation in SingleSpurProblem. The solution makes an interesting use of Stacks, if you would like to check it out. This problem is a bit more challenging than what I could put on a homework.

Interested in more insight into the sequence 1, 2, 5, 14, 42, 132, 429, 1430, 4862, ... ? Check out https://oeis.org/A000108.

1.5 Daily Questions

So far, three daily questions are behind us. I have fully scored question 1 (and am trying to figure out how to get these results into Canvas). I have scored a subset of the next two questions, and this effort will soon involve the TAs in the class so I can keep up with these daily questions.

Q1: In your own words, why is BINARY ARRAY SEARCH guaranteed to eventually stop and return either true or false? Ans: Within the while loop, either it returns TRUE or low is increased to a larger value or high is decreased to a smaller value. If target is not found, eventually low becomes greater than high and the loop exits.

Note: A bad algorithm can make the same claim but not achieve performance of BINARY ARRAY SEARCH: NotBinaryArraySearch.

Q2: I showed a naive implementation to find largest:

largest = 0 for i = 0 to n-1 if A[i] > largest largest = A[i] print "largest is", largest

This uses N comparison, but this algorithm is not correct (as many you of you caught) because all values in A could be negative, and this code would return the wrong result.

Q3: So why is the tournament algorithm SLOWER than the native algorithm when it is run? Ans: Here is one of the best answers:

The tournament algorithm is theoretically faster than the native algorithm when comparisons are the only time object taken into account. However, there is a lot more data necessary to be stored in the tournament algorithm than the native algorithm. This fact causes the tournament algorithm to in practice actually run slower than the native algorithm. Comparisons are not the only aspect of the timescale for programs

1.6 Data Type vs. Data Structures

In addition, you can’t even resize most arrays. The best you can do is create a new array that is larger (or smaller) than the original one, and then you copy elements from the original array into the new structure. The obvious conclusion is that resizing a stack takes time directly proportional to the stack size. This point will come up later this lecture.

This distinction is important because we are going to use arrays to implement a number of data types, starting with Stack

1.7 Fixed Capacity Stack Implementation

You have seen FixedCapacityStackOfString implementation (p. 133). If you continue with p. 135 you will see an implementation that uses the Java Generics capability to define a Stack of any type of element. Functionality is the same, this is just easier to program with.

The generic implementation can be found in the Git repository, in class FixedCapacityStack where it uses generics.

public class FixedCapacityStack<E> { private E[] a; // holds the items private int N; // number of items in stack // create an empty stack with given capacity public FixedCapacityStack(int capacity) { a = (E[]) new Object[capacity]; N = 0; } public boolean isEmpty() { return N == 0; } public boolean isFull() { return N == a.length; } public void push(E item) { a[N++] = item; } public E pop() { return a[−−N]; } }

Here are some questions to ask

Are you familiar with N++ and −−N operators?

What does the field N represent? Can you put it in words?

Can you make the E[] a field have the final modifier?

Can you make the int N field have the final modifier?

The biggest limitation is that this will run out of the existing memory, so we need a strategy to deal with expanding storage on demand.

1.8 Expandable Fixed Capacity Stack Implementation

Pages 136-137 describe how to resize the stack as needed to ensure it grows to support the full set of objects being pushed onto the stack. This implementation is efficient for several reasons:

• Memory efficient – once popped, the former value in the array location is set to null. This improves Garbage Collection. But also makes it easier to understand within the debugger.

• Amortized constant performance – A tricky statistical consideration.

The goal, as stated by Sedgewick, is to ensure that "push and pop operations take time independent of the stack size." (p. 132). How can you be sure this is true if you know that resizing the stack takes time directly proportional to the stack size.

Statistics to the rescue!

Let’s say you did N operations, and each one took a fixed amount of time. For simplicity, we’ll call this a single unit of time, without regard to whether it is seconds or hours in length. Once completed, these N operations will have taken up N units of time

1 + 1 + 1 + 1 + ... + 1 + 1 = N time units

So the average is N/N or 1 time unit.

All good so far. What if some operations take longer? For example, what if each successive operation takes one more unit of time than the previous? With N operations, you would then have

1 + 2 + 3 + 4 + ... + N-1 + N = N*(N+1)/2 time units

Here the average is (N+1)/2 time units. No longer is the time of an operation considered to be independent of other operations. In addition, the average is no longer a constant number.

Now let’s review the behavior of Stack. As long as the stack is not full, you can be assured that each push or pop operation will take time "independent of stack size", so it can be treated as a single time unit.

Now, what if you could guarantee that given a sequence of N operations, N-1 of the operations would require a single time unit while just one would require N time units. Note it is important that the N is the same value (both to count the number of operations and to reflect the length of the time to perform). The reason is that this special operation would take time to perform "in time that is dependent on the size of the input" (to twist the statement on page 132).

Now your summation becomes:

1 + 1 + 1 + 1 + ... + 1 + N

That is, 1 added N-1 times, and N added one final time. The total is 2N-1 operations, which when divided by N is 2-1/N which can be considered to be a constant especially with increasing values of N.

How do you ensure this nice distribution? First, let’s review the code (which I have placed in ResizingArrayStackResizeStrategies. Here is the revised push function (a bit simplified from my actual code which is instrumented to show why this strategy is the right choice.

public void push(Item item) { if (N == a.length) { resize (2*a.length); } a[N++] = item; // add item }

Here’s the thing. Empirical studies have consistently shown that this is the best approach when you have no idea as to the number of elements that will be pushed onto the stack.

ResizingArrayStackResizeStrategies demonstrates the benefit. When you compare two separate runs, how much SLOWER is the one that only extends linearly, say by 100 positions?

Resize by extending by 100 positions Time: 0.06300 (size = 59982, #Resize = 600) Avg=0.03316 +/- 0.01404 Time: 0.03200 (size = 59950, #Resize = 600) Avg=0.00954 +/- 0.01216 Time: 0.04600 (size = 60292, #Resize = 603) Avg=0.01759 +/- 0.01105 Time: 0.03200 (size = 60146, #Resize = 602) Avg=0.00665 +/- 0.00973 Time: 0.03100 (size = 60226, #Resize = 603) Avg=0.01305 +/- 0.01278 Resize by doubling Time: 0.00000 (size = 60004, #Resize = 15) Avg=0.00000 +/- 0.00000 Time: 0.01600 (size = 60254, #Resize = 15) Avg=0.00996 +/- 0.00776 Time: 0.00000 (size = 60152, #Resize = 15) Avg=0.00000 +/- 0.00000 Time: 0.01600 (size = 60296, #Resize = 15) Avg=0.00951 +/- 0.00786 Time: 0.00000 (size = 60070, #Resize = 15) Avg=0.00000 +/- 0.00000

public Item pop() { if (isEmpty()) throw new NoSuchElementException("Stack underflow"); Item item = a[N-1]; a[N-1] = null; // to avoid loitering N–; if (N > 0 && N == a.length/4) { // shrink size of array resize(a.length/2); // if necessary } return item; }

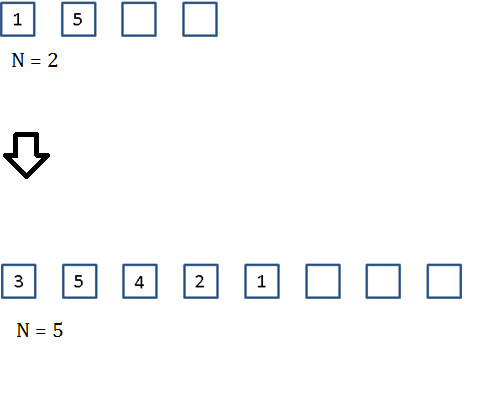
1.9 In-class question

You are given a stack of elements with storage of size 4 and containing two elements as shown. Propose a sequence of operations that results in the revised stack with storage of size 8 and containing 5 elements as shown.

Figure 1: Open Discussion

1.10 Iteration

Review the discussion on page 138-139 which describes how to traverse all elements of an aggregate data type. In this case, the structure is an array, so a ReverseArrayIterator is developed as an inner class to ResizingArrayStackResizeStrategies.

Briefly, why does a Stack need a reverse array iterator instead of a regular forward iterator?

Note in the Lecture help session today (3PM Friday in FL PH-UPR) I will go over the Iterator code. This will be recorded, so if you can’t make this special help session, you will be able to review the video when you can.

You can review the ArrayIterator sample code I have provided for iterating in forward direction over an array of elements.

1.11 Analysis of Experimental Data: Order of growth

Sedgewick presents the case for running benchmarks on your data to determine runtime performance. From this data, you can determine trends by plotting the results.

The goal is to determine Order of Growth for performance (p. 180). Here is sample output for DoublingTest, comparing results from 2015 and 2018.

These results were run on three different computers, but they exhibit, more or less, the same growth pattern. What can you make of these numbers? Perhaps you might use Excel to compute Trendlines for the available data.

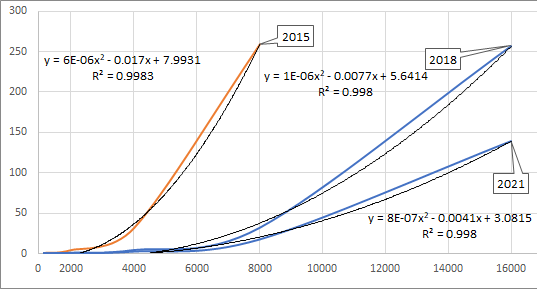
Using this model, you might be able to estimate the time it would take to perform the computation with N=32000 elements. The difference in specific values from column-1 to column-3 reflect the improved hardware performance (and perhaps other factors) since the code is identical.

Develop mathematical model (following upon Knuth’s foundations) that the running time of a program is determine by:

• Cost of executing each statement

• The frequency of execution of each statement

Sedgewick uses Tilde approximation which abstracts most code blocks into constant execution, relying on identifying the most frequently executed operations. Typically these are deep within a nested for loop, or you can determine the number of recursions that a recursive function call makes.

1.12 Demonstration: Anagram Reborn

To show the new algorithm, here is a pseudocode fragment. You will be asked to work with pseudocode this term, whether in class, or on a homework or on an exam so it is good to become comfortable with this notation.

In pseudocode, you can have variables and functions. Loops and if-then-else conditionals are also available. You use natural English fragments to describe computations, and use pseudocode to demonstrate high-level control flow.

Find the implementation within AnagramFinal. Show demonstration.

That’s right. It now takes 2 seconds to find an anagram of the 15 letters. This is the power of algorithms: Taking a brute-force computation from 31 days down to 2 seconds. 2,678,400 seconds down to 2 seconds. A million-fold speedup!

One way to see why it has improved so much is to review the first twelve words that each one checks.

ORIGINAL NEW britneyspears britneyspears britneyspeasr britenyspears (save 8! = 40320) britneysperas britynespears (save 8! = 40320) britneyspersa britsneypears (save 8! = 40320) britneyspesar britsenypears (save 7! = 5040) britneyspesra britsynepears (save 7! = 5040) britneyspaers britspneyears (save 7! = 5040) britneyspaesr britseneypars (save 7! = 5040) britneyspares britsaneypers (save 7! = 5040) britneysparse britsrneypeas (save 7! = 5040) britneyspaser britssneypear (save 7! = 5040) britneyspasre britpneysears (save 8! = 40320)

Admittedly, this speed-up occurs because the dictionary of english words actually provides a boost by allowing us to filter out huge chunks of the computational space. If English had ten-times as many words, with more prefix-similar words, then the resulting effort would still require factorial permutations.

Can you do better? Last year one student submitted a solutio that found an anagram for "GRADS TENSE SHINE" in just 40 milliseconds! How is this possible?

With my original solution (2 seconds) I was able to optimize the code to get my solution down to 89 milliseconds. This twenty-fold speed up was achieved by structuring the data differently to increase the overall speed of my implementation.

1.13 Sample Exam Question: solved

There is an alternate notation known as postfix notation. The above equation would be represented as "1 4 5 * 2 3 + * +". As its name implies, in postfix notation the operator comes after the arguments. Based on the structure of Dijkstra’s algorithm, devise a one stack solution to compute the value of this sequence of tokens.

On the exam, I would ask you to describe this algorithm using pseudocode:

This only shows for "+" and "*" but you can clearly see how to extend to other binary operators. This would be a suitable answer on an exam.

stack = new Stack while more input available s = next token if s is "*" then pop off last two values from stack and push back their product else if s is "+" then pop off last two values from stack and push back their sum else if s is value then push numeric interpretation of s onto stack pop value from stack and print it out

1.14 Sample Exam Question

This question assumes that you have a Stack of elements.

Write pseudocode for a function that takes a Stack of elements and modifies the stack so that its bottom two elements are swapped with each other.

1.15 Lecture Takeaways

• Arrays can store aggregate information. For dynamic behavior, you can both grow and shrink array.

• Homework 1 Rubric is posted

1.16 Thoughts on Homework 1

So far my office hour attendance has been more social than answering questions that students have. This might mean that students are taking care of business and do not have lots of questions. Of course it could also mean that you do have questions, but you are going to the TA office hours (great!). If, however you haven’t started the homework yet, please take my advice and delay no longer...

1.17 Lecture Challenges

Given the 10 base-10 digits (0, 1, 2, 3, 4, 5, 6, 7, 8 and 9) can you construct a mathematical expression solely of addition that produces the value 100?

For example, 18 + 29 + 30 + 4 + 5 + 6 + 7 = 99. So close! Note how each digit is used exactly once. In trying to solve this problem, try to make statements of fact that you can use to guide your solution. For example, you could start by realizing that no three digit number would ever be used, because that is already over the target total of 100.

1.18 Daily Question

The assigned daily question is DAY04 (Problem Set DAY04)

If you have any trouble accessing this question, please let me know immediately on Discord.

1.19 Version : 2021/03/30

(c) 2021, George T. Heineman