CS 2223 Dec 10 2015

Lecture Path: 24
Back Next

Expected reading:
Daily Exercise:

If you don’t know where you are going, you’ll end up someplace else.
Yogi Berra

1 All Pairs Shortest Path Lecture

We have completed the presentation of Single-Source Shortest Path. You have seen this in class and you are also working on your own implementation using an adjacency matric implementation for homework5.

Naturally this leads to the next question, namely identifying the shortest path between any two vertices in a digraph. Because of the nature of directed edges, it may be the case that there are some vertices that are unreachable from other vertices.

Given the existing solution DijkstraSP which computes single-source shortest path, we repeat the execution for each vertex to produce an array of solutions all[].

public class DijkstraAllPairsSP { DijkstraSP[] all; /** Computes all shortest path solutions. */ public DijkstraAllPairsSP(EdgeWeightedDigraph G) { all = new DijkstraSP[G.V()]; for (int v = 0; v < G.V(); v++) all[v] = new DijkstraSP(G, v); } /** Returns a shortest path from vertex s to t. */ public Iterable<DirectedEdge> path(int s, int t) { return all[s].pathTo(t); } /** Returns the length of a shortest path from s to t. */ public double dist(int s, int t) { return all[s].distTo(t); } /** Determines if path exists. */ public boolean hasPath(int s, int t) { return dist(s, t) < Double.POSITIVE_INFINITY; } }

Ok, so now it is time to perform a time analysis of DijkstraSP so we can understand the time analysis of DijkstraAllPairsSP.

1.1 Review Example

Handout contains small example to be worked on. During this execution, you are keeping track of a distTo[] array and a pq priority queue, where each vertex in the priority queue is assigned a value; smaller values mean the vertex is closer to the front of the queue. Ties are broken arbitrarily.

1.2 Performance Analysis

Review the handout for today in which we go over this algorithm.

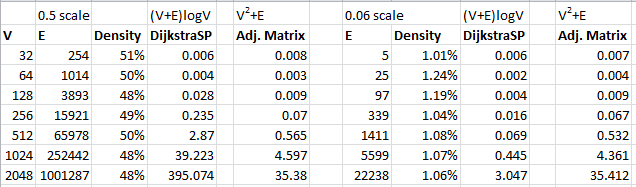
It turns out that the Tilde Approximation for DijkstraSP is (V+E)*log V while the Tilde Approximation is V2+E for the adjacency matrix implementation for the same algorithm.

Which should you choose? Depends on the number of edges, doesn’t it?

We are now ready to introduce the official notation used throughout computer science theory (and practice) to define the execution performance of algorithms. It is officially known as asymptotic notation but informally it is known as Big Oh notation.

We use O-notation to give an upper bound on a function, to within a multiplicative factor. You have already seen this idea with regard to Tilde Approximation. We will continue to do so but now with a new notation.

You have seen this (ever so briefly) in the HW5 description of the algorithm. We say the performance is O(f(...)) where the function f declares the order of growth.

1.3 Exam preparation

The final exam is scheduled for one week from today. This examination is cummulative. Once again, you will be able to bring a single piece of paper on which you can write whatever you want to help you during the exam. This is an opportunity for you to collect your thoughts and organize the material on paper (as well as in your head).

Here is the structure:

Question 1: Short answer with explanations. Be sure you offer an explanation since you will lose points if you only provide the specific answer.
Question 2: Performance consideration. Given a sample algorithm you will be asked to evaluate its performance
Question 3: Algorithm Design. You will be asked to design an algorithm to solve a given problem.
Question 4: Example solution. You will be given a small problem to solve and show your work.
Question 5: Type question. In this you will be able to demonstrate your knowledge of the fundamental types used in this course: bag, stack, queue, priority queue, binary search trees.

1.4 Status Injective Graphs Exploration

To give a sense of the scale of graph problems, consider creating random undirected graphs with N vertices. How many such graphs exist? Given N vertices, there are N*(N-1)/2 possible edges. If each of these can exist independently of each other, then there are 2N*(N-1)/2 possible undirected graphs. If N=9, then N*(N-1)/2 = 36 which means there are 236 possible undirected graphs, or 68,719,476,736.

I am currently running a Status Injective Explorer to find all 9-vertex graphs that are status injective. I’ve tried this over a number of days and I have been constantly thwarted by Microsoft auto-update that reboots my machine during the night when applying updates.

Nonetheless, I am counting about 100,000 SIJ graphs every 70 seconds of wall time. I have currently counted 107,000,000 possible SIJ graphs, but I don’t know when this will complete because I should be clocking the number of graphs being checked, rather than the number of SIJ graphs computed. I will let you know tomorrow.