►CS 2223 Dec 11 2015
1 Big O Notation Completion
1.1 Empirical Evidence
1.2 Loop performance analysis
1.2.1 Nested Loops With Integer indices
1.2.2 Graph Looping Analysis
1.3 Major concerns
1.4 Master Theorem
1.4.1 Find maximum recursively
1.5 Other complexity families
1.6 Summary
1.7 Version : 2015/ 12/ 14

CS 2223 Dec 11 2015

Lecture Path: 25
Back Next

Expected reading: pp. 638-657
Daily Exercise:

There should be no such thing as boring mathematics
Edsger Dijsktra

1 Big O Notation Completion

1.1 Empirical Evidence

You will routinely execute your programs and then graph its progress:

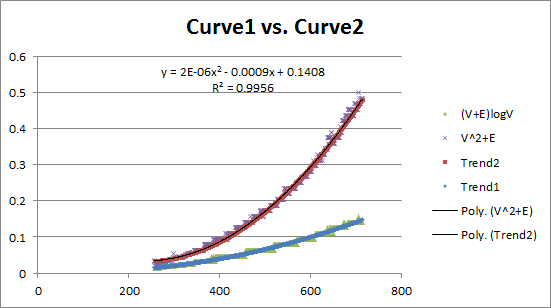
These two curves reflect the two different single-source shortest path algorithms presented yesterday. Observe that they have different growth behaviors, but can this be used to empirically confirm the theoretical results as shown yesterday?

The performance of the algorithm (on average) appears to be hitting the mark very close to expected. But what happens in the worst case? Indeed, what is the worst case for each of these algorithms?

We want to be able to identify three cases for each algorithm:

For the duration of this lecture, we will be solely interested in worst case performance.

1.2 Loop performance analysis

Regular loops are easy to handle, but we need to take special care with nested loops (including for/while) as well as the latest loops seen with graph structures.

1.2.1 Nested Loops With Integer indices

We have seen several types:

for (int i = 0; i < N; i++) { for (int j = 0; j < N; j++) { statement } }

The above statement will execute N2 times, and this naturally extends to higher orders:

for (int i = 0; i < N; i++) { for (int j = 0; j < N; j++) { for (int k = 0; k < N; k++) { statement } } }

Here the statement executes N3 times. What if the indices are more dynamic?

for (int i = 0; i < N; i++) { for (int j = i+1; j < N; j++) { statement } }

We have seen this format also. When i is 0, statement executes N-1 times, when i is 1, statement executes N-2 times, and so on. It turns out you need to compute the sum of the numbers from 1 to N-1 to determine the proper number of executions of statement. These are the triangular numbers, that is, the Nth triangle number is N*(N+1)/2. In this case we are looking for the N-1th triangle number (starting from N=1) which means the proper computation is N*(N-1)/2 times.

Here is a more complicated situation

for (int i = N; i > 1; i /= 2) { for (int j = 0; j < N; j++) { statement } }

Here the outer i loop executes exactly floor(log(N)) times. What about the inner loop? It continues to execute N times, thus the total number of times statement executes is: N*floor(log(N))

1.2.2 Graph Looping Analysis

Now that we have seen the graph structure, there are more complicated patterns of behavior.

for (int u = 0; u < g.V(); u++) { for (int v = 0; v < g.V(); v++) { statement } }

The inner statement executes V2 times. This is true regardless of whether g is a directed or undirected graph.

However, it is more common to see something like this for an undirected graph.

for (int u = 0; u < g.V(); u++) { for (int v : g.adj(u)) { statement } }

How to interpret in this case? Well, you know that the outer u for loops is going to visit each vertex exactly once. Then the inner v loop visits each neighbor of u.

What about recursive executions, such as dfs? What is the perform of dfs(g, 0)? In this case, Graph is undirected. Note that whenever I refer to a directed graph, I will always call it a Digraph.

void dfs(Graph G, int v) { marked[v] = true; for (int w : G.adj(v)) { if (!marked[w]) { edgeTo[w] = v; dfs(G, w); } } }

First observe that the recursive call only happens because there is an unmarked vertex; after each recursive call the vertex is marked, so you know that the depth of the recursion is never more than V, the number of vertices in the graph. Now, how many times does the if (!marked[w]) statement execute? Well, assuming that you can retrieve the neighbors of a vertex in time directly proportional to its degree, then this statement executes twice for every edge E.

For a directed graph, the if (!marked[w]) statement would execute once for every edge E.

A similar argument can be made for breadth first search:

void bfs(Graph g, int s) { Queue<Integer> q = new Queue<Integer>(); marked[s] = true; q.enqueue(s); while (!q.isEmpty()) { int v = q.dequeue(); for (int w : g.adj(v)) { if (!marked[w]) { edgeTo[w] = v; marked[w] = true; q.enqueue(w); } } } }

The queue contains marked vertices. As each one is dequeued, its neighbors are checked; if any of them are unmarked, they are added to the queue. Thus once a vertex is marked it won’t be added back into the queue, which means the dequeue method is called no more than V times. In an undirected graph the inner if (!marked[w]) statement executes twice for every edge E in the graph.

1.3 Major concerns

We used Sedgewick’s Tilde expressions to rapidly approximate the execution performance of an algorithm, or to compute the number of times a key function (such as compareTo) executed.

The goal was to evaluate the worst case behavior that would result for an algorithm and to classify the algorithm into a well known performance family. We have seen several of these families to date. We now can classify their order of growth (in the worst case) using the following notation:

But what does this terminology mean? we need to turn to asymptotic complexity to answer that question:

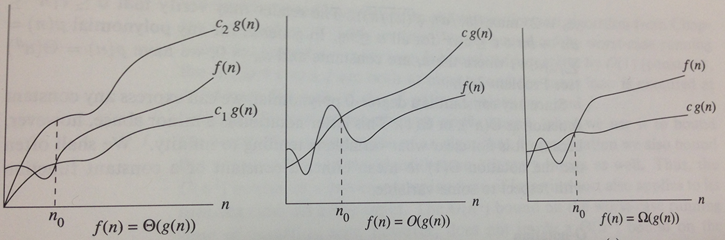
The above picture has a curve f(n) that represents the function of interest. The value n represents, typically, the problem size being tackled by an algorithm. As you can see, the value of f(n) changes over time, increasing when n increases.

The goal is to classify the rate of growth of f(n) and we use a special notation for this purpose, which looks awkward the first time you see it.

There are three notations to understand:

Once an algorithm is thoroughly understood, it can often be classified using the Θ() notation. However, in practice, this looks too "mathematical". Also it can’t be typed on a keyboard.

So what typically happens is that you classify the order of growth for the algorithm using O(g(n)) notation, with the understanding that you are using the most accurate g(n) classification.

To explain why this is necessary, consider someone who tells you they have a function to find the maximum value in an array. They claim that its performance is O(2n). Technically they are correct, because the rate of growth of the function (which is linear by the way) will always be less than some constant c*2n. However, there are other classifications that are more accurate, namely O(n).

And it is for this reason that all multiplicative and additive constants are disregarded when writing O() notations. Specifically, the constants matter with regard to the specific runtime performance of actual code on specific problem instances. Programmers can improve the code to reduce the constants, that is, making the program run faster in measurable quantities. However, theoretically, there are limits that programmers can achieve. And the overall order of growth, or rate of growth, is fixed by the design of the algorithm.

1.4 Master Theorem

We have seen a number of recurrence equations in this course, which are of the following form:

T(n) = aT(n/b) + f(n)

There are a number of special cases that can be handled by this theorem.

1.4.1 Find maximum recursively

We have already seen this algorithm for finding the maximum value in an array of N elements.

static Comparable largest (Comparable[] a, int lo, int hi) { if (hi <= lo) { return a[lo]; } int mid = lo + (hi - lo)/2; Comparable maxLeft = largest (a, lo, mid); Comparable maxRight = largest (a, mid+1, hi); if (less(maxLeft, maxRight)) { return maxRight; } else { return maxLeft; } }

When computing the number of comparisons used in this function, that can be described by

C(N) = 2*C(N/2) + 1

If you assume n is a power of 2 (to simplify the argument) then

C(N) = 2k*C(N/2k) + 2k-1 + 2k-2 + ... + 1

Note that C(N) = 0 and if you expand this out you get:

C(2n) = 2n-1 + 2n-2 + ... + 1

which equals N-1

From the original statement of the recurrence, however, this result could have been determined.

The master theorem declares how to compute these results without carrying out the telescoping process.

In particular, let a >= 1 and b > 1 be constants, and let f(n) be a function. Now define T(n) on the non-negative integers by the recurrence

T(n) = aT(n/b) + f(n)

And we interpret n/b to be either floor(n/b) or ceiling(n/b) as appropriate. We are trying to find the asymptotic bound for T(n) as n grows.

The key intuition is comparing f(n) with regards to nlogb(a). That is, you divide problem of size n into sub-problems of size n/b and then you perform a of them. When a < b, logb(a) < 1. However, if you perform a > b subproblems, then you will eventually begin to pay the cost, and you have to account for it.

In the recursive maximum computation, a = b = 2, which is a common case. That is,

T(n) = 2*T(n/2) + f(n)

Note that logb(a) in this case is log2(2) which is 1. So in this common case, what are the possible results?

*whew*

Why does this matter?

Well, if you found a recurrence of the form:

T(n) = 2*T(n/2) + Ω(n log n)

then you know that T(n) = Θ(n log n).

Ask yourself why the recursive functions don’t have additional work that requires sorting of the results? The reason is simply that the extra work performed during the recursion cannot be ignored and it will eventually build up to overwhelm the benefit of splitting the problem recursively.

You can use this same formula to compute the performance cost of the three-way merge sort which subdivided a problem into three sub-problems (thus, b=3 and a=3 also).

1.5 Other complexity families

There is a class of problems in computer science that have defied any efficient solution in a reasonable amount of time. These are known as the NP-Complete problems.

One example is called the "Hamiltonian Cycle" problem. Given an undirected (or directed) graph, compute a path that visits every vertex in the graph exactly once and then returns to the starting vertex.

While this problem looks very similar to the check whether a graph is connected, it cannot be solved without generating all possible paths. I will wave my hands for a bit and suggest that the number of possible paths in an undirected graph is proportional to N!

You can try your hand on sample random graphs in the HamiltonianCycle code example. This is similar in structure to the anagram solver, since it tries all possible paths.

1.6 Summary

You can find numerous online resources about the Big O notation. Here is one convenient one that I have found:

The Big-O Cheat Sheet

1.7 Version : 2015/12/14

(c) 2015, George Heineman