9.7 High_Level Data Flow Analysis
We can perform data flow analysis on a tree when the tree is known to represent the program flow(e.g., no multiple entries and exits from loops, no GOTO's etc.).
The following live variables analysis is described by Babich and Jazayeri (1978a). They compute dead variables and available expressions. We will discuss dead variables. Exercise 9 asks the reader to write the equations for available expressions and reaching definitions.
A variable is defined as dead at a point in a program if its value will not be used after control leaves that point.
The following (ambiguous) grammar will be used:
StatementStatement1 Statement2 Statement
IF Expression THEN Statement1 ELSE Statement2 Statement
WHILE Expression DO Statement Statement
Label : Statement Statement
GOTO Statement Statement
Assignment Statement
ReadStatement Statement
WriteStatement
The following notation will be used for the tree nodes:
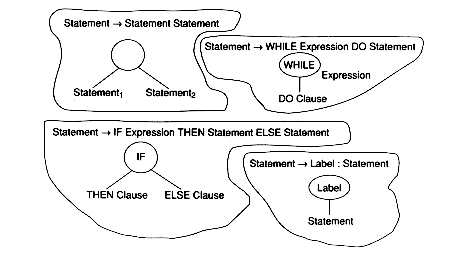
Four Boolean attribute, Kill, Gen, DeadAtBeginning and DeadAtEnd, will be associated with each of these nodes. For simplicity, only one variable will be analyzed. Exercise 7 asks the reader to extend this for more than one variable. The equations will reflect the following:
Statement.DeadAtBeginning := True if the variable is Dead at the beginning of Statement.
Statement.DeadAtEnd := True if the variable is DEAD at the end of Statement.
Statement.Kill := True if the variable is assigned a value in Statement.
Statement.Used := True if the variable is used and not assigned in Statement or else used in statement before being assigned in Statement.
We will define these first two more precisely below. The algorithm will iterate because none of the methods we have developed so far will work (see Exercise 6).
Since deadness at a point is inherently a property of the portion of the program that comes after that point, we need to have sacnned the portion of the program that that node. Thus, we scan the tree from right to left.
The attributes DeadAtBeginning and DeadAtEnd are defined as follows:
For Assignment, Read, and Write Statements:
-
Statement.DeadAtBeginning := NOT(Statement.Used) AND (Statement.Kill|Statement.DeadAtEnd)
For Statement  Statement1 Statement2, we note that we want to start with the
value of Statement.DeadAtEnd and compute Statement.DeadAtBeginning and that
the end of Statement1 is also the beginning of Statement2. Therefore,
Statement1 Statement2, we note that we want to start with the
value of Statement.DeadAtEnd and compute Statement.DeadAtBeginning and that
the end of Statement1 is also the beginning of Statement2. Therefore,
Statement2.DeadAtEnd := Statement.DeadAtBeginning
and since the end of Statement1 is also the beginning of Statement2,
Statement1.DeadAtEnd := Statement2.DeadAtBeginning
The beginning of Statement1 is the same point as the beginning of Statement, so:
Statement.DeadAtEnd := Statement1.DeadAtBeginning
The equation for IF statements and WHILE statements are similar. The attribute grammar is:
(1) StatementStatement1 Statement2 (i) Statement2.DeadAtEnd := Statement.DeadAtBeginning (ii) Statement1.DeadAtEnd := Statement2.DeadAtBeginning (iii) Statement1.DeadAtEnd := Statement2.DeadAtBeginning (2) Statement
IF Expression THEN Statement1 ELSE Statement2 (i) Statement2.DeadAtEnd := Statement.DeadAtEnd (ii) Statement1.DeadAtEnd := Statement.DeadAtEnd (iii) Statement.DeadAtBeginning := NOT (Expression.Used) AND (Statement1.DeadAtBeginning AND Statement2. DeadAtBeginning) (3) Statement
WHILE Expression DO Statement (i) Statement.DeadAtEnd := NOT (Expression.Used) AND (Statement.DeadAtEnd AND Statement1.DeadAtBeginning) (ii) Statement.DeadAtBeginning := NOT (Expression.Used) AND (Statement.DeadAtEnd AND Statement1.DeadAtBeginning) (4) Statement
Label : Statement (i) Statement1.DeadAtEnd := Statement.DeadAtEnd (ii) Statement.DeadAtBeginning := Statement1.DeadAtBeginning (5) Statement
GOTO Statement (ii) Statement.DeadAtBeginning := TargetStatement.DeadAtBeginning (6) Statement
Assignment | ReadStatement | WriteStatement (i) Statement.DeadAtBeginning := NOT (Statement.Used) AND (Statement.Kill | Statement.DeadAtEnd)
For the WHILE loop the rules for Statement1.DeadAtEnd and Statement.DeadAtBeginning are the same because an exit from the body of a WHILE loop is followed by a branch back to reenter the loop.
It may be necessary to compute the attributes at a node more than once before the correct values are computed. The (recursive) algoritm to compute attribute values for each statement is:
-
Algorithm
Dead (statement)
BEGIN {Dead}
FOR each component of Statement,
in right to left order,
BEGIN
Compute Component.DeadAtEnd
Call DEAD (Component)
END
Compute Statement.DeadAtBeginning
END {Dead}
The values for DeadAtEnd and DeadAtBeginning are saved in the tree as they are computed. Thus each tree node contains at least the following information:(1) node type (compound, IF, WHILE, etc.), (2) the values of DeadAtEnd and DeadAtBeginning, (3) assorted pointers to other nodes, describing the position of the node in the tree and (4) values of Used and Kill where needed.
In a pass over the tree, attributes whose values are needed will usually be computed before they are used. In two cases, however, this will not be true. The first case is backward GOTO's since the right to left scan will not have computed the right-hand side of the semantic function. The second case is for WHILE statements since to find DeadAtEnd, we need DeadAtBeginning, which isn't know because Statement1 hasn't been analyzed yet. Because of these two cases, we initialize these attributes to True.
The evaluation algorithm iterates until no attribute value changes.
-
Algorithm
Dead(Tree)
While there are changes to any attribute value DO
Initialize attributes to True
BEGIN
Store Root.DeadAtEnd and Call Dead(Root)
Store any changed values
END
Example 12 shows a program and the values after two passes over the tree, analyzing the attribute values for the variable A.
EXMAPLE 12 High-level data flow analysis example
Read A
WHILE B < > 0 DO
BEGIN
Write A
WHILE A < 5 DO
BEGIN
A := A + 1
Write A
B := A
END
Read (A)
END
Pass 0( Initializing Attributes to True):

Pass 1

Example 12 shows the initialization pass and pass 1 of the evaluation. The reader is asked to perform the remaining passes in Exercise 8.
