9.5 Reached Uses
Reached uses is a similar problem to live variable analysis.
A Use of A is reached from the assignment statement A := if there is some path from the assignment to the use along whitch A is not redefined.
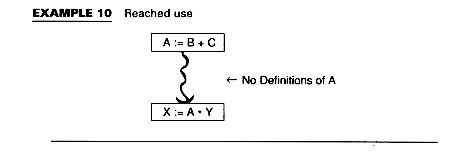
We can detect useless assignments: they are those assignments with no reached uses.
To find the equations for reached uses, note that the last definition of A in a block B reaches what the end of block B reaches, plus subsequent uses of A within B. Prior definitions of A within B reach only their uses within B.
Equations for Reached Uses
The domain is somewhat different here: the set of pairs consisting of a statement S and a variable A appearing on the right of S.
Kill(B) = {(S,A) | S not in B and B contains an assignemnt to A}
Gen(B) = {(S,A) | S 
B, A on right-hand side of S, and no definitions of A prior to S in B}
Transfer Equation
In(B) = (Out(B) - Kill(B)) 
Gen(B)
Confluence Equation
-
Out(B) =
In(S)
-
S
Succ (B)
The algorithm is essentially the same as that for live variables; that is, we assume nothing is reached, and apply the equations. The result is the smallest solution since a use is reached only if we can really find a path to it.