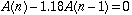 Where A(n) is the balance in
the nth month.
Where A(n) is the balance in
the nth month.[WPI] [cs2223] [cs2223 text] [News] [Notes] [Recurrence] [Word]
W1. 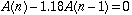 Where A(n) is the balance in
the nth month.
Where A(n) is the balance in
the nth month.
W3. When the nth person joins, n-1
others send messages. 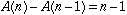
W4. Form an n-letter word by adding a letter
to an n-1 letter word. Consider two cases for words of length n-1:
words containing only B-Z (to which Z can be added) and all other acceptable
words containing A (to which only A-Y can be added). In the first group,
the letters are all B-Z so there are 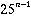 words, to which Z can be added.
In the second group, there are A(n-1) words, to which any
of 25 letters can be added. The number of n-letter words is:
words, to which Z can be added.
In the second group, there are A(n-1) words, to which any
of 25 letters can be added. The number of n-letter words is: 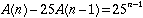
W5. Subsets of Sn can be broken into two groups:
those that don't include n-1 (to which n can be appended without
causing consecutive integer conflict) and those that do include n-1
(to which n cannot be appended). The first set is just A(n-2)
and the second set is A(n-1). The number of subsets is: 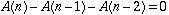 This
is the fibonacci sequence.
This
is the fibonacci sequence.
W6. There are two ways to arrange boxes on a shelf of
size n: add a shoebox to the end of a shelf of size n-1 or
add a boot box to the end of a shelf of size n-2. The number of arrangements
is: ![]() Again, this is the fibonacci sequence.
Again, this is the fibonacci sequence.
W8. The average value on day n-1 is
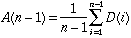
and the average on day n is
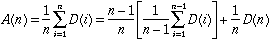
The recurrence relation is 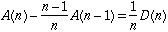
W9. At each step, pieces 1/3 of each edge of the snowflake perimeter is removed and replaced by two pieces of the same size. Thus each piece is replaced by segments of total length 4/3 the original length. Adding together all of the pieces, the recurrence relation for the perimeter is:
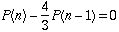
And, new triangles (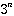 of them) each with area
of them) each with area 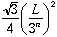 , is added to
the snowflake area. The resulting recurrence relation is:
, is added to
the snowflake area. The resulting recurrence relation is:
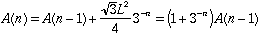
W10. Products of even numbers are even; products of odd numbers are odd. Thus the recurrence relation that works for both even and odd numbers is:
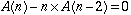
![]()
![[WPI Home Page]](../../../images/wpi_logo_small.gif) |