cs2223 Word Problem Examples

[WPI] [cs2223] [cs2223 text] [News] [Notes] [Recurrence]

cs2223, D97/98 Recurrence Word Problem Examples

These examples contain word descriptions of problems or algorithms. You can use them to practice writing recurrence relations. Try to work the problems before looking at the solutions.

W1. [Solution] Your bank charges 18% per month interest on the ourstanding balance on your Visa card. If you have a balance of $1.00 and you absent-mindedly forget to pay such a small balance, how much will you owe the bank in 35 years?

W2. [Solution] Redo W1 but include a $60 annual bank fee (charged in 12 monthly increments).

W3. [Solution] Imagine an e-mail system which is only used to greet people who join the system. Thus, when the first person joins, no e-mail is sent. When the second person joins, one message is sent (from the first to the second), and so on. What is the total number of messages that has ever been sent after the 100th person joins?

W4. [Solution] How many words of length n can be formed using the 26 letters {A-Z} with the condition that the letter Z never appears after an A?

W5. [Solution] Consider a set Sn of consecutive integers of size n. How many subsets of Sn contain no consecutive integers?

W6. [Solution] Shoe boxes come in two sizes: shoes fit in a shoe box and boots fit in a boot box that is twice as wide as a shoe box. In your shoe store you have shelves that are big enough to hold n shoe boxes. How many arrangements of shoes and boots can you display?

W7. [Solution] In a certain game, your gain (or loss) at the nth round is The game has been rigged so that you alternate winning and losing. What is your cumulative total after n rounds?

W8. [Solution] The Dow Jones stock market index on day n of the year is D(n). What is the yearly average value A(n) on day n?

W9. [Solution] The Koch snowflake is a transformation of an equalateral triangle. At each step, each edge is trisected and a smaller (1/3 the length) equalateral triangle is constructed in its place.

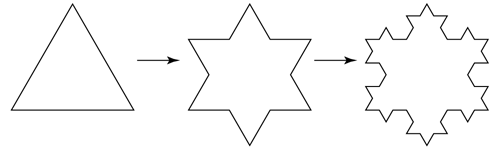
Calculate P(n), the perimeter at the nth step and A(n), the area at the nth step when the starting length is L. Notice that the values for the starting triangle (n=0) are:

W10. [Solution] Let Sn be the set of all positive integers less than or equal to n. Find the largest possible product Pn of the elements of Sn with this property: if n is even, Pn is even; if n is odd, Pn is odd.