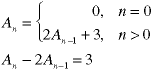
[WPI] [cs2223] [cs2223 text] [News] [Notes] [Recurrence] [Solving] 

cs2223, D97/98 Solving Recurrence Relations - Step 1

Find the Homogeneous Solution

Begin by putting the equation in the standard form. That means all terms containing the sequence go on the left and everything else on the right. Here is "mathemetician" notation and "standard notation" for the same recurrence relation:

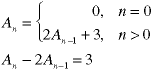
A(n) = {0, n=0 or 2*A(n-1) + 3, n>0; A(n) - 2*A(n-1) = 3

Set the RHS (right hand side) to zero to form the homogeneous equation. That equation describes how the sequence evolves in the absence of any "forcing function" - the stuff in the RHS. The solution is the homogeneous solution. Here is how you find it.

Guess that the solution is of this form:

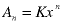
A(n) = K*x^n

At this point, don't worry about what K and x are, just consider them to be constants whose values are not yet known. Substitute this guess into the homogeneous equation and solve for x:

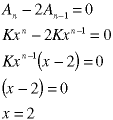
A(n) - 2*A(n-1) = 0; K*x^n - 2*K*x^(n-1) = 0; K*x^(n-1)*(x-2) = 0; (x-2) = 0; x=2

Thus the homogeneous solution is:

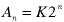
A(n) = K*2^n

The undetermined coefficient K can be any finite number - they are all solutions of the homogeneous equation;

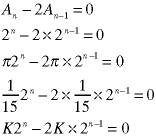
A(n) - 2*A(n-1) = 0; 2^n - 2*2^(n-1) = 0; pi*2^n - 2*pi*2^(n-1) = 0; (1/15)*2^n - 2*(1/15)*2^(n-1) = 0; K*2^n - 2*K*2^(n-1) = 0

The equation for x is called the characteristic equation. It can be derived from just looking at the recurrence relation;

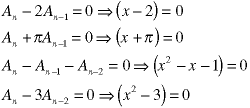
A(n) - 2*A(n-1) = 0 -> (x-2) = 0; A(n) + pi*A(n-1) = 0 -> (x+pi) = 0; A(n) -A(n-1) - A(n-2) = 0 -> (x^2 - x - 1) = 0; A(n) -3*A(n-2) = 0 -> (x^2 - 3) = 0

The order of the characteristic equation is the same as the order of the recurrence relation. When it is of first order, the solution is simple.

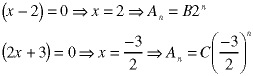
(x-2) = 0 -> x = 2 -> A(n) = B*2^n; (2*x + 3) = 0 -> x = (-3/2) -> A(n) = C * (-3/2)^n

When the characteristic equation is of second order, the solutions can be found by factoring:

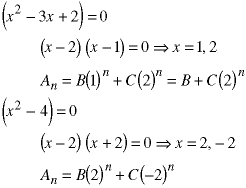
(x^2 - 3*x + 2) = 0; (x-2) * (x-1) = 0 -> x = 1, 2; A(n) = B*(1^n) + C*(2^n) = B + C*2^n;(x^2 - 4) = 0; (x-2) * (x+2) = 0 -> x = 2, -2; A(n) = B*2^n + C*(-2)^n

There are two undetermined coefficients because the equations are of second order. The standard quadratic method can be used if the factoring is not obvious:

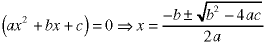
(a*x^2 + b*x + c) = 0 -> x = (-b +/- sqrt(b*b - 4*a*c)) / (2*a)

Here are a few examples:

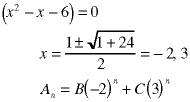
(x^2 - x - 6) = 0; x = (1 +/- sqrt(1 + 24)) / 2 = -2, 3; A(n) = B*(-2)^n + C*3^n

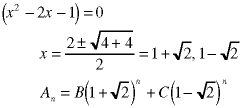
(x^2 - 2*x - 1) = 0; x = (2 +/- sqrt(4 + 4)) / 2 = 1 + sqrt(2), 1 - sqrt(2); A(n) = B*(1+sqrt(2))^n + C*(1-sqrt(2))^n

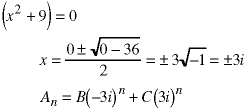
(x^2 + 9) = 0; x = (0 +/- sqrt(0 - 36)) / 2 = +/- 3*sqrt(-1) = 3*i, -3*i; A(n) = B*(-3*i)^n + C*(3*i)^n

Don't worry if the roots are irrational, imaginary, or complex. When the values of the coefficients are determined at the very end, the resulting sequence values, An, will be real.

If the characteristic equation is of third-order or higher, finding the roots can be problematic. Mathematical tables, symbolic mathematical software, or numerical root-finding programs can sometimes be useful.

Repeated Roots

Some characteristic equations give multiple copies of the same root:

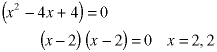
(x^2 - 4*x + 4) = 0; (x-2) * (x-2) = 0; x = 2, 2

In that case, just put n in front of one of the roots in the solution:

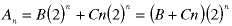
A(n) = B*2^n + C*n*2^n = (B + C*n)*2^n

We can directly substitute this into the recurrence relation to show that it is the correct answer;

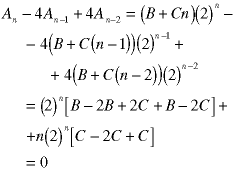
A(n) - 4*A(n-1) + 4*A(n-2) = (B + C*n) * 2^n - 4 * (B + C(n-1)) * 2 ^ (n-1) + 4 * (B + C(n-2)) * 2^(n-2) = 2^n * (B -2*B + 2*C + B - 2*C) + n*2^n * (C - 2*C + C) = 0

Here is another example:

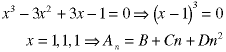
x^3 - 3*x^2 + 3*x -1 = 0 -> (x-1)^3 = 0; x = 1, 1, 1 -> A(n) = B + C*n + D*n^2

Now that we know how to find the solution to the homogeneous equation, we are ready to go on to Step 2, finding the particular solution.--------------------
[WPI Home Page] [cs2223 home page]  [cs2223 text] [News] [Notes] [Recurrence] [Solving] 

Contents ©1994-1998, Norman Wittels
Updated 19Mar98