[WPI] [cs2223] [cs2223 text] [News] [Notes] [Recurrence] [Solving]
This is the part of the total solution which depends on the form of the RHS (right hand side) of the recurrence relation. Guess a solution of the same form but with undetermined coefficients which have to be calculated. We find their values by inserting the particular solution into the recurrence relation.
This recurrence relation:
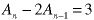
has a constant in the RHS, so guess the particular solution of the same form (a constant);
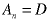
Substitute this back into the recurrence relation and solve for the unknown coefficient, D.
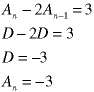
This is only part of the total solution. If it bothers you that we didn't include the homogeneous solution when we solved for the unknown coefficient (the one from the particular solution), recall that the homogeneous solution always sums to zero (that's how we found it!) so it can have no effect on the calculation of D:
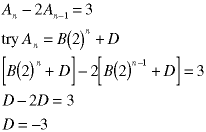
For the rest of this web page, we will ignore the homogeneous solution when we are solving for the coefficients in the particular solution. But, as we will show later, you must know the homogeneous solution before guessing the particular solution.
The form of the particular solution has nothing to do with the order of the recurence relation. It only depends on the form of the RHS.
| RHS | Guess this Particular Solution |
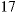 (constant) (constant) |
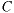 (constant) (constant) |
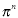 (constant to the nth power) (constant to the nth power) |
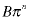 (constant to the nth power) (constant to the nth power) |
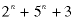 (linear combination) (linear combination) |
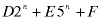 (same linear combination) (same linear combination) |
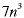 (polynomial in n) (polynomial in n) |
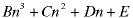 (decreasing polynomial) (decreasing polynomial) |
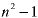 (polynomial) (polynomial) |
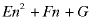 (decreasing polynomial) (decreasing polynomial) |
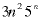 (linear combination) (linear combination) |
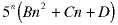 (linear combination) (linear combination) |
Notice how a polynomial in n produces a decreasing polynomial with all orders down to, and including, the constant term. Without those extra terms, the coefficients cannot usually be determined successfully.
Look at this recurrence equation:
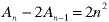
If we try a single-term guess, watch what happens:
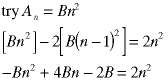
There is no way to eliminate the n, so we cannot solve for B. Now try a complete descending polynomial:
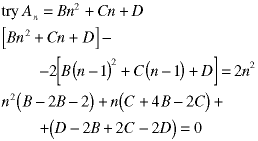
In order for the solution to be independent of n, each of the three terms above has to equal zero. That gives us three equations in three unknowns - B, C, and D, The solution is:
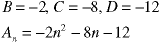
Again, this is only the particular part of the solution, it has to be added to the homogeneous solution to form the total solution, as we will show in Step 3.
There is a slight complication when the RHS is already of the form of the homogeneous solution. Look at this example:
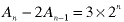
We cannot try a particular solution of the form:
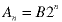
Because that is already a homogeneous solution so the left side will sum to zero. We get around this problem using the same trick as when we found the homogeneous solution; multiply the guess by n:
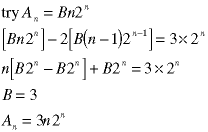
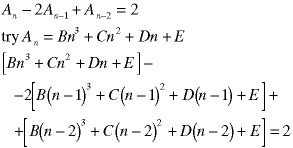
Note, we didn't neeed the B term in the solution - the repeated root is of second order so we only needed to have three terms in the guess (two for the repeated root and one for the constant on the right side). But, pretend we don't notice that and see what happens:
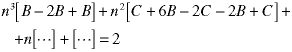
There is no reason to proceed. When we set each term to zero, the first tells us nothing and the second tells us that B equals zero. So, let's try again, using a simpler guess:
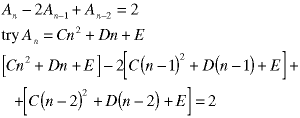
Setting each term to zero, we get this solution:
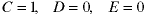
The last two parts of the solution may not seem obvious from looking at the above mathematics, but the equations show that D and E can have any values. This means that either they are already part of the homogeneous solution. The best solution is to set any such ambiguous coefficients to zero.
We can reach the same result by looking at this sequence of trial solutions, in which we try a constant, then a constant times n, etc.:
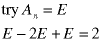 |
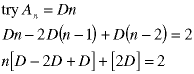 |
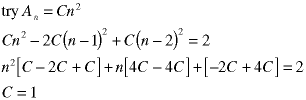 |
The first two show that the a constant or a constant times n cannot be the particular solution. But, we already knew that because their linear combination forms the homogeneous solution. The third shows that a constant times n-square can be a particular solution so, by uniqueness, it must be the particular solution.
Some people find it easier to solve polynomial particular solutions by beginning at the top (at the order of the RHS, or above if the RHS is of the form of the homogeneous solution) and eliminating terms until the solution is found. Some people fine it easier to begin at the bottom (try a constant, first-power of n, second-power of n, etc.) until the solution is found. Pick which works best for you. In any event, if you find a set of coefficients which works, that is the soluion. If you cannot find a consistent set of coefficients, you guessed poorly. There will be no undetermined coefficients in the particular solution - if you have any, then what you found isn't the particular solution.
![]()
![[WPI Home Page]](../../../../images/wpi_logo_small.gif) |