cs2223 Class 8

[WPI] [cs2223] [cs2223 text] [News] [Syllabus] [Classes]

cs2223, D97/98 Class 8

Note: This page contains an attached Excel spreadsheet. A zip version is also atached for those whose browsers do not reliably download spreadsheet files.

Tower of Hanoi Redux

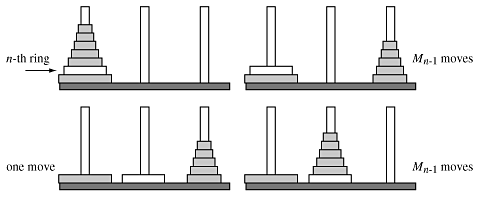
In Class 7. we looked at one way of solving the Towers of Hanoi problem. Here is a somewhat different approach which gives a different recurrence relation but the same answer: Moving the top n rings from one rod to another is equivalent to this sequence: move the n-1 rings above it to the third rod, move the n-th ring, then move the stack of n-1 rings so they are back on top of the n-th ring:

Figure showing the moves described above

The recurrence relation is:

and the solution is.

Page 1 of the attached spreadsheet shows, by direct calculation, that the first fifty terms of the two recurrence relations match each other and the solution.

Binary Search

The linear search method of finding whether a number is in an array - start at the beginning looking for a match; if you run off the end of the array, it isn't there - is not a particularly effecient search method. If the array has n elements, the best possible search takes one comparison, the worst takes n, and the average case takes n/2 comparisons. A more efficient search method is to presort the array and use the binary search method.

If we know the data are ordered, the best place to start is in the middle of the array. Depend on whether the number we are looking for is higher or lower than the number at the midpoint, we jump to the midpoint of that half, and so forth until the number of the step size is one.

[Figure illustrating the above algorithm]

In this example, the bad news is that we looked for the number 23 and didn't find it. The good news is that it only took three comparisons, instead of the eight which would be required to reach the same conclusion, if we used a linear search. Here is how to compute the worst case number of comparisons - that is the case in which the search is not successful, the number is not found. One comparison is made each time we cut the search region in half so the recurrence relation for comparisons is:

This does not fit either of the forms we identified as "relatively easy to solve" in the recurrence relation notes, so we need a trick. We will use substitution of variables. The problem with the recurrence relation is the variable step size between the two terms - the relation can be first-order, second-order, fourth-order, eight-order, etc, but not third order. By substituting the variable k for lgn we obtain this recurrence relation:

n = 2^k <--> k = lg(n); C(2^k) - C(2^(k-1)) = 1

Nothing has changed except that the terms now appear in some sort of sequence - specifically the exponents of two are sequential. Let's form another sequence of terms, B_k, and match them up with the C_k.

Each B_k is uniquely identified with a C_k - if you know one you know uniquely which is the corresponding value. Here is why we went to this trouble. The C_k are not sequential - there are gaps between them when going from k to k+1. The B_k, however, are sequential - there are no gaps. Thus we can solve the recurrence relation for B_k.

Notice how we used the initial condition on C_n - when there is one element in the array it takes one comparison to see if that is the number we are seeking - to form the corresponding initial condition on B_k. Recall that lg(1)=0. Now we go backward through the process to find what we want - C_n

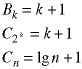
B(k) = k + 1 -> C(2^k) = k + 1 -> C(n) = lg(n) + 1

The second page of the attached spreadsheet shows that this solution matches the original recurrence relation for the first 12 terms. We discussed that this search algorithm is inherently recursive. The code for a recursive binary search algorithm is s contained in the CCC directory

/cs/cs2223/classes/class08/

and the attached script shows its operation.

Fibonacci sequence

Consider this recurrence relation:

We can use the characteristic equation method to find the solution:

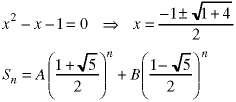
x^2 - x - 1 = 0 -> x = (-1 +/- sqrt(1 + 4))) / 2;
S(n) = A*((1+sqrt(5))/2)^n + A*((1+sqrt(5))/2)^n

To find A and B we need two initial conditions. Here is an example.

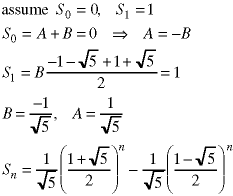
S(0)=0, S(1)=1 -> A = 1/sqrt(5), B = -1/sqrt(5) ->
S(n) = (1/sqrt(5)) * ((1 + sqrt(5))/2)^n - (1/sqrt(5)) * ((1 - sqrt(5))/2)^n

The third page of the attached spreadsheet shows that this solution gives the correct values for the first one hundred terms in the sequence.

Notice that this solution contains irrational constant coefficients times powers of irrational constants yet the terms come out integral, for integer values of n. Âlso, note that the sequence this solution produces - 0,1,1,2,3,5,8,13,... - is the "usual" fibonacci sequenc. But it is not the only fibonacci sequence. So is

In fact any sequence - integer, rational, real, or complex - in which each term is the sum of the prior two is a fibonacci sequence.

Fibonacci sequences show up often in computer science. Consider the problem of parking cars and busses in a parking lot with n spaces, if cars take up one space and busses take up two. Suppose we want to calculate -A_n the number of arrangements of cars and busses in a parking lot of size n. There are two ways we can fill n spaces: we can add one car to the end of a lot with n-1 spaces or we can add one bus to the end of a lot with n-2 spaces. This produces the recurrence relation.

The solution is a fibonacci sequence with the initial conditions A1=1 (the only arrangement is one car) and A2=2 (two arrangements - two cars or one bus). The resulting sequence is 1, 2, 3, 5, ...