cs2223 Class 6

[WPI] [cs2223] [cs2223 text] [News] [Syllabus] [Classes]

cs2223, D97/98 Class 6

Note: This page contains an attached Excel spreadsheet. A zip version is also atached for those whose browsers do not reliably download spreadsheet files.

Proofs

There are three types of proofs commonly used in analyzing algorithms - direct proofs, indirect proofs, and inductive proofs. These notes compliment the material in Chapter 1 of the text.

Direct Proof

The direct proof combines known true statements (definitions or theorem, which are statements proven to be true) to produce other new statements.

The definitions of even and odd in the system of integers are:

If there exists some integer i such that the integer n = 2i, then n is even
If there exists some integer j such that the integer n = 2j+1, then n is odd

37 is an odd number

In order to prove that 37 is odd, we need merely to find an integer j which fulfills the definitiion of oddness. That number is j=18, so 37 is odd.

Indirect Proof

Whenver you are trying to prove that something doesn't exist, the indirect proof, or proof by contradiction, is almost always used. Thatis because proof of non-existence using direct proofs would require a very large - usually infinite - number of proofs. You would have to show that each of the possible answers doesn't work in order to prove there is no answer to the question. The indirect proof reaches the same result but in a different way. There are three steps:

Take a collection of known true statements (definitions and theorems). "Known true" means there are no contradictions between them. For example, if combining the statements shows that 1=0, that would be a contradiction.
Add another statement whose tis in question. This is usually a statement we want to disprove, so it is the opposite of what we really want to prove.
Look for any contradictions. If one is found, the new statement must be false, which makes it opposite - what we really wanted to prove - true.

No integer can be both even and odd

For example, let's prove that no integer can be both even and odd. Assume that there is such an integer, n, which is both even and odd - this is our added statement, the opposite of what we want to prove. Then, using the definitions above, we can write n two different ways and combine them.

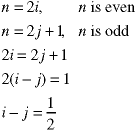
n=2i (n is even);
n=2j+1 (n is odd);
2i=2j+1; 2(i-j)=1;
i-j = 1/2

This is a contradiction. We have shown that the difference between two integers is a number which is not an integer. But the set of integers is closed under the operation of addition - that means that the difference between any two integers has to be an integer - so this is a contradiction. Thus the statement "there is a number which is both odd and even" has been proven to be false so the statement "there is no number which is both odd and even" is true.

No two successive integers can have the same divisor except one

Prove that no two successive integers have a common divisor - except one, which is a divisor for all integers. Begin by assuming that there are two succesive integers, n and m, which have a common divisor j.

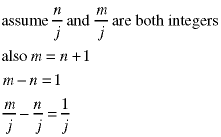
assume n/j and m/j are both integers and that m=n+1;
m-n=1;
m/j - n/j = 1/j

Again, we have the same contradiction - the difference between two integers is a non-integer. We have proven that no two successive integers can have a common divison.

Euclid's proof

Prove there is no largest prime number - which is equivalent to proving there are an infinite number of prime numbers. A prime number is is an integer which cannot be divided by any other integer except itself or one. Assume that P_N is the largest prime number. Then form the number R - the product of all of the prime numbers - and add one to it.

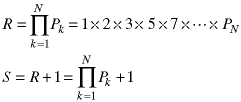
R = prod(k=1->N; P(k)) = 1*2*3*5*7*...*P(N); S = R+1 = prod(k=1->N; P(k)) + 1

By the last theorem (proof), S cannot be divided by any of the prime numbers, so it must be prime. This is a contradiction, so we have provent here is no largest prime number.

Proof by Induction

The proof by induction is used to produce a sequence of proofs.

Arithmetic Series

For example, here are two definitions of A_n. Proving that they are equivalent for all positive values of n, requires a sequence of proofs - one for each value of n. Instead, we would use an inductive proof.

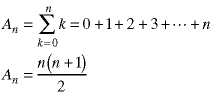
A(n) = sum(k=0->n; k = 0+1+2+3+...+n;
A(n) = n * (n+1) / 2

There are two parts to the inductive proof.

The basis step. This is a demonstration that there is one case for which the proof is true. Both of the above equations, produce the same answer, A₀=0, so the basis step is established.
The inductive step. We assume the n-th proof in the sequence is true. If we can use this assumption to show that the n+1-th step is also true, then we have completed the proof, and have shown that all proofs in the sequence are true.

Look at both definitions of A_n and extend them to the next step in the sequence, using the assumption that they are equivalent at the n-th step. If the new expressions are equivalent, then the inductive step has been completed.

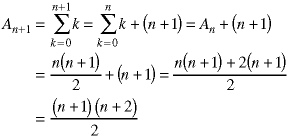
A(n+1) = sum(k=0->n+1; k) = sum(k=0->n; k) + (n+1) = A(n) + (n+1) = n*(n+1)/2 = (n+1) = (n*(n+1) + 2*(n+1))/2 = (n+1)*(n+2)/2

This result is exactly what we obtain when we replace n by n+1 in the second definition of A_n so we have shown the two definitions to be equivalent. This is known as the arithmetic series. Page 1 of the attached spreadsheet shows that the definitions of the first 100 terms are equivalent. It does not, however, show that all of the terms are equivalent - only a proof can do that.

Another related series

Consider this statement.

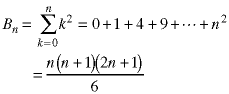
B(n) = sum(k=0->n; k^2) = 0+1+4+9+...+n^2 = n*(n+1)*(2*n+1)/6

The second page of the attached spreadsheet shows that this is true for the first 100 terms in the sequence. Can you prove this is true for all values of n>0?

Geometric series

Prove this statement, the solution of the geometric series.

G(n) = sum(k=0->n; a^k) = (1 - a^(n+1)) / (1 - a) when abs(a) < 1

When n=0, both sides give A₀=1, so the basis step is established. The inductive step is:

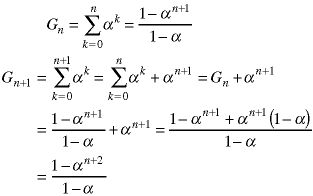
G(n) = sum(k=0->n; a^k) = (1 - a^(n+1)) / (1 - a);
G(n+1) = (1 - a^(n+1)) / (1-a) + a^(n+1) = (1 - a^(n+1) + a^(n+1) * (1-a) / (1-a) = (1 - a^(n+2)) / (1-a)

This result is exactly what we obtain when we replace n by n+1 in the second definition of A_n so we have proven that the definitions are equivalent. The third page of the attached spreadsheet shows that this is correct for the first 100 terms in the sequence (to within the accuracy of Excel).

Selection Sorting

The selection sort was described on pages 62 and 106 of the text. We go through an array taking each element in sequence and looking for the smallest number in the rest of the sequence. If a smaller number is found, we swap the two numbers. The result is a sorted array.

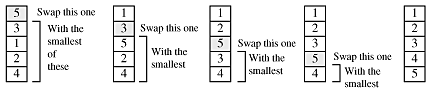
illustration of the sorting process

Here is a sorting function which uses this algorithm.

void selection(int n, int *array) // selection sort an array
	{
	int temp;
	for (int i = 0; i < n - 1; i++)
		for (int j = i + 1; j < n; j++)
			if (array[j] < array[i])
				{
				temp = array[i]; // swap the values
				array[i] = array[j];
				array[j] = temp;
				}
	return;
	} // end selection()

We want to calculate the number of comparisons made by the command

			if (array[j] < array[i])

and the number of swaps, which is just the number of times that the comparison evaluates as true.

We can replace the for statements by summations to calculate the number of comparisons for an array of size n:

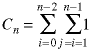
C(n) = sum(i=0->n-2; sum(j=i+1->n-1; 1))

We used the fact that there is one comparison per time through the inner loop. The solution, which uses a result from the discussion about summations in Class 4 and the geometric series from above, is:

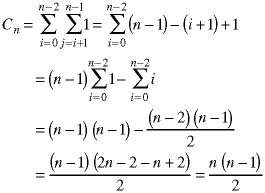
C(n) = sum(i=0->n-2; sum(j=i+1->n-1; 1)) = sum(i=0->n-2; (n-1) - (i+1) + 1)) = (n-1) * sum(i=0->n-2; 1) - sum(i=0-.n-2; i) = (n-1)*(n-2) - (n-2)*(n-1)/2 = (n-1)*(2*n - 2 - n + 2)/2 = n*(n-1)/2

The function selection() was put into a simulation program. The source code is in the CCC directory:

/cs/cs2223/classes/class06/

The attached script shows operation of the program. Note that the simulation also shows that the number of swaps in the best case - the data were already sorted - and the worst case - the data were in inverse order - are exactly what we predicted in class.