The explosive growth of mailing lists, Web sites and Usenet news
has caused information overload. It is no longer feasible to search through all
the sources of information available in order to find those that are of
interest to an individual user.
Collaborative filtering systems recommend items based upon opinions of people
with similar tastes. Collaborative filtering overcomes some difficulties
faced by traditional information filtering by eliminating the need for computers
to understand the content of the items. Further, collaborative filtering can also
recommend articles that are not similar in content to items rated in the past as
long as like-minded users have rated the items. Unfortunately, collaborative
filtering is not effective when there are too few users that have rated an item
or for users that do not have a strong history or correlation with other users.
Content-based systems use content to filter or recommend items. These perform
well when users know and specify topics in which they are interested.
Recommendations for a user are based solely on a profile built by analyzing the
content of the items which that user has rated in the past. Content based filters
face problems of over-specialization. When the system can only recommend items
scoring highly against a user's profile, the user is restricted to seeing items
similar to those she has already seen. Also, it is often difficult for
content-based filters to understand the meaning of text or even the actual content
of complex items.
We combine the strengths of content-based filtering techniques with collaborative
filtering to provide more accurate recommendations. We use thresholds to improve
the accuracy of traditional filtering algorithms, and design and implement a
way to apply content-based filtering to an online newspaper. We compare our improved
algorithms to current algorithms using both off-line and online experiments and show
that these result in more effective filters that can help manage the massive amount
of information that is confronting us today.
I would like to thank my thesis advisor Prof. Mark Claypool for his
advice and support throughout this entire project. Thank god they still
make such advisors! I would also like
to thank Prof. George Heineman, Prof. Carolina Ruiz and
Prof. Sergio Alvarez for bearing with me at all the times I have
burst into their office for guidance or ideas.
I am also grateful to my friends, Chandrakant Natarajan, Jens Peter
Kaps and Andreas Koeller, my roommates Charu Vepari and
Allegra Treaster and my office mate Peter Leveille for
helping me maintain my sanity during the tough times and for tolerating
me when I occasionally crossed the line between genius and madness!
Last but not least, I would also like to thank my parents for deciding
to come for my graduation thus leaving me with no option but to graduate
in time !
Recent years have seen the explosive growth in the amount of
information. The amount of information available through books,
movies, news, television programmes, advertisements, and in
particular on-line sources, such as email, Usenet News, Web
documents, is staggering. An individual cannot hope to absorb even
a tiny fraction of today's information, and, to make things worse,
more information is added daily!
The World Wide Web started in 1990
and grew to over 10,000 Web sites by December 1994 [RIS94]
and to 650,000 Web sites by January 1997 [Gra99]. Together
these servers exported a minimum of 1.05 million documents.
Furthermore, studies in 1996
have shown that the Web is filled with transient information.
In 1996, there were an estimated 50 million pages on the Web and each
page was online for only an average of 75 days. Other recent
surveys have estimated the number of Web users
in the U.S. as of May 1998 at 57,037,000 and the number of Web pages as
of April 1998 at approximately 320 million [Tre98b]!
Furthermore, the number of pages is doubling every year. Using
the average Web page size of 30 kilobytes (including graphics)
brings the current size of the Web to 1.5 terabytes (or
million megabytes).
Usenet News is also growing exponentially. Estimates show that in May 1993
there were over 2.6 million users of Usenet News at almost 87,000 sites
that generated over 26 thousand new articles a day [Tre98a]. A year
later, the estimated number of users on Usenet News had risen to almost
10 million. Other surveys have also estimated a 140 percentage increase in the
number of on-line auction sites listed by Yahoo from April to June,
1997 [Tre98a].
Studies have also shown that on average, a video store holds
about 5,000 video titles, a music radio station holds about
10,000 LPs and CDs [Sta99]. The Library of Congress
contains about 20 million books.
The adoption of media like the email by corporations, governmental and
educational institutes and the widespread use of newsgroups further
compounds the problem of information overload.
These media, being effective means for fast coordination, dissemination
and retrieval of information, bring with them the problem of information
overload. Information overload
in new electronic media stems from the skewed relationship between the
costs of the sender of the information and those of the recipient in
relation to other media. Once the sender has created the information,
the cost (in both money and effort) of sending it to many recipients
is relatively low. The problem (from the recipients point
of view) with electronic media is that they shift virtually all the power
from the recipient to the sender. This shift in power makes it very
important to develop automatic techniques to filter information at the
recipients side. It is impossible to access or read all the
information out there.
The need for automated techniques to cope with so much information
has become very important. Automated techniques are needed to prioritize the
information that a user is able to access (or that
gets sent to her) so that the user can make effective use of her time
to read the information that might be most relevant to her.
Collaborative filtering is a general approach to personalized
information filtering.
Collaborative filtering automates the process of recommending items
to a user based upon the opinions of people with similar tastes.
In most cases, the filtering system determines which users have similar
tastes by using standard formulae for computing statistical correlations.
In other systems, users can additionally specify the users whose ratings
should be considered while computing the prediction.
Collaborative filtering has been present socially and implemented on a human
level each time people have based their actions (for example, going for a
particular movie) on the feedback received from people they normally
agree with (for example, the opinion of a close friend or neighbor).
Today's networked computers allow collaborative filtering to apply
to more and more users.
This technique helps a user build correlation with every other user
depending on how much she agrees with them and then uses a combination
of this correlation and their feedback on particular items to help
her filter out or prioritize her items. Take the example of a
user making a decision on the movie she wants to go and see. If
there is a way for the user to find all the people who have similar
tastes about movies, she could make a much better decision about the
movie to see by basing her decision on the opinions of all these people
instead of relying on the opinions of a few friends.
Many collaborative filtering techniques use a form of weighted average
to determine a prediction for a user [BP98, , , FD92, ]. These techniques use the
correlation (degree of similarity between two users) as the weights.
Every user receives a prediction for all items and submits a rating
of how well she likes a
item after reading it. This feedback given by her is used along with
similar feedback from other users to calculate a rating prediction. The
feedback given by the user along with the rating prediction received by
her for a particular item is later used to update her degree of
correlation with every user.
The effectiveness of collaborative filtering
techniques relies on the confidence on the computation of the
``similarity'' between users. Further, the more the number of
``similar'' users, the more effective the prediction will be
as having more users can minimize the inconsistencies/errors
that could arise if a user agreed with another on most topics
except a few. For example, if user A agreed on most things
with user B except that user A liked romantic comedies and B
hated them, then it would lead to an inaccurate prediction if
A relied only on user B's rating for romantic comedies. We
shall henceforth refer to improvements suggested to current
collaborative filtering techniques to improve the accuracy
of the predictions as tuning of collaborative
filtering techniques.
Current collaborative filtering techniques make predictions
without taking the history between users into account.
These systems neither threshold on the history between users nor assign
any weights to the history so that users with stronger histories
can influence the prediction more than other users. A user is given
a prediction based on the ratings of users who may not have
seen enough items in common to be able to justify making a strong
prediction based on their ratings. For example, if user A and B have seen only
one item in common and have agreed, it is not a strong basis to
predict that they will agree on the rating given to the second item, too.
Current techniques also do not favor those people that have a strong
history and cannot give more importance to ratings of users
who have agreed over a larger number of articles and so are more likely
to agree in the future. We shall henceforth refer to these issues as the
History Problem.
Another reason for tuning is that current techniques make
predictions even if the number of users (or raters) whose
ratings are utilized are less than a particular threshold. For example,
if an item has been seen by just one user, it could potentially
be a ``weak'' rating. There is a possible risk of computing an
inaccurate prediction for an article if only one user had rated it
and the article happened to be on a subject that the user in question
and the user who rated it disagreed on even though the two users had
a high correlation over all topics.
One way to solve this issue is to be able to let the system give a
stronger prediction even if the number of people who have read
the article and have a correlation with the user is low. This is
possible if the system bases the prediction on the content of the
article also. We shall henceforth refer to this issue as the
Weak Rating Problem.
Furthermore, current collaborative filtering systems do not use the
content of the article as a factor in determining its relevance.
Predictions are entirely based on correlation between other users.
If a user wants articles on ``collaborative filtering''
to be given a high prediction, she cannot specify that articles with
particular content (in this case ``collaborative filtering'') be always
given a higher rating. This means that a user cannot setup
specific profiles so that articles with certain keywords would be given
higher rating predictions by the system. She is also unable to specify
just how much she wants the information content to control a rating
prediction. For example, she may want items marked as at least average
by other users and containing the words
``collaborative filtering'' to be given a higher prediction. Therefore,
we also need to integrate current traditional content-based filtering
techniques with collaborative filtering to provide a user with a more accurate
prediction under all circumstances. We shall henceforth refer to this
issue as Content Problem.
Lastly, tuning is also required for cases where current techniques
provide predictions outside the range of valid ratings. Current collaborative
filtering algorithms can face situations where the computed prediction
falls outside the range of ratings that a user can give to an article.
In such cases there is no clear definition of how to interpret these
predictions that are above or below the valid range. For example, if a
prediction of 7 is mapped to 5 (5 being the highest possible on a scale of
1 to 5), it is unclear how a user should interpret a prediction of 5 that
was not re-mapped. This reduces the confidence that a user can place
in a prediction. We shall henceforth refer to this issue as
the Normalization Problem.
We implement modifications to current weighted average algorithms to
solve the problems outlined above. We improve accuracies in predictions
arising due to the History Problem by enforcing thresholds on the
number of articles seen in common by any two users. Ratings of users who
have seen articles less than the thresholds with the user in question
are not considered for the computation of the prediction. We also impose
similar thresholds on the correlation between two users so that only users
who have very similar/dissimilar opinions influence the
predictions. We evaluate our modifications to the basis algorithm on data
sets extracted from the Eachmovie data set [EM97]. In addition, we analyze
the characteristics of collaborative filtering data sets.
We devise techniques for content filtering of the news articles and for the
integration of the collaborative and content filtering predictions.
In order to evaluate our approach to the content problem, we built a filtering
system that combines collaborative and content based filtering
on newspaper articles from a local online newspaper (Telegram and Gazette). We
ran this system with a test bed of 18 users who rated newspaper articles
for two months and collected and analyzed performance data.
In summary, the main contributions of our work are:
We design and develop a more acurate collaborative filtering algorithm
by implementing correlation and history thresholds on a basis algorithm.
We show that our algorithm is also more consistently accurate.
We show that the implementation of both history and user
thresholds is most effective when these thresholds are user specific.
We show that the integration of pure collaborative filtering with content
based filtering improves the accuracy of the prediction specially in the startup
phase of a collaborative filtering system.
We also show that the integration of collaborative filtering techniques
with content based filtering allows the collaborative filtering system to
compute the prediction for new users or for other users who haven't rated enough
articles to have a correlation with any other user.
We show that the absolute size of the data set and the total
number of ratings in the data set is not a good indicator of the
accuracy of the collaborative filtering system. The accuracy of the predictions
depends more on the number of rated items in common between users
than on either the total number of items in the system or the absolute number
of items seen and rated by any user.
In Chapter 2, we look at related work
in information filtering in general and collaborative filtering
specifically.
In Chapter 3, we discuss the various
improvements we propose to the base algorithm and our experiments
to evaluate our improvements.
In Chapter 4, we discuss our approach to
integrating collaborative filtering techniques with content
based filtering techniques and our experiments to evaluate our
aproach.
Lastly, we present our conclusions in Chapter 6 and
recommend areas for future work in Chapter 7.
The general problems of information overload have received considerable
attention in research literature. Research in the general area of solving
information overload problem can be broadly categorized into
information filtering techniques and information retrieval.
We shall use the term information filtering generically to refer both
to finding desired information (filtering in) and eliminating that which
is undesirable (filtering out).
Malone et al. describe three categories of filtering techniques,
cognitive, social, and economic, based on the information sources the
techniques draw on in order to predict a user's reaction to an article
[MGT87]. The three categories provide a useful
road map to other literature on filtering techniques. In the recent past,
work has also been done on systems that use a combination of any two
or all three of the above categories. We shall refer to these as
hybrid techniques and shall discuss some of the work done in
this area.
Cognitive, or content-based, filtering techniques select documents based on
the text in them. For example, the kill files and string search
features
provided by Usenet news clients perform content filtering. More sophisticated
techniques might also filter out articles from people who previously
co-authored papers with an objectionable person. Even the division of
Usenet news into newsgroups is a primitive example, since a reader restricts
her attention to those articles with a particular text string in their
``newsgroup:'' field. Strings could also be combined with the Boolean
operators AND, OR, and NOT.
Alternatively, the profile of what to filter in or filter out could consist
of weight vectors, with the weights expressing the relative importance
of each of a set of terms [DDF90, FD92, PR91].
In standard ``keyword-matching'' vector systems [PS79], textual
databases are represented by a ``word-by-document'' matrix whose entries
represent the frequency of occurrence of a word in a document. The
similarity between documents is computed as the inner product or cosine
of the corresponding two columns of the word-by-document matrix. The words
are considered to be pairwise independent.
Latent Semantic Indexing(LSI) [DDF90, ] does not consider
the words to be pairwise independent. In LSI, the associations among
terms and documents are calculated and exploited in retrieval. A description
of terms, documents, and user queries based on the underlying latent semantic
structure is maintained. Users can thus retrieve relevant documents even if
they do not have any words in common with the query.
Some content filtering techniques update user profiles automatically based
on feedback about whether the user likes the articles that the current
profile selects. Information retrieval research refers to this process as
relevance feedback [SB98]. It has been shown that user inputs about
concepts related to those mentioned in an initial query, together with their
relative importance, can significantly improve retrieval effectiveness
[SB98]. Relevance feedback can be improved if users select
features from the texts of relevant documents [CD90], instead of limiting
them to selecting concepts from lists of terms selected automatically from
relevant documents by the system (the system extracts these concepts by
applying natural language processing techniques to the descriptions of
interests that the user provides). The techniques for updating profiles
can draw on Bayesian probability [BC92], genetic algorithms
[SB90], or other machine learning techniques.
Social filtering techniques select articles based on relationships between
people and on their subjective judgments. A moderated newsgroup employs a
primitive form of social filtering, choosing articles for all potential
readers based on evaluations by a single person, the moderator.
Collaborative filtering, based on the subjective evaluations of other readers,
is an even more promising form of social filtering. Human readers do not
share computers' difficulties with synonymy and context when
judging the relevance of text. Moreover, items being filtered need not
be amenable to parsing by a computer. People can judge texts on other
dimensions such as quality, authoritativeness, or respectfulness.
The Tapestry system makes more sophisticated use of subjective
evaluations [HHWM92b].
In Tapestry, many people can post evaluations, not just a single moderator,
and readers can choose which evaluators to pay attention to. Moreover,
filters can combine content-based criteria and subjective evaluations.
For example, a reader could request recipes containing the words ``romantic
comedies'' that user B has evaluated and where the evaluation contains the
word ``good''. Tapestry, though, does not include aggregate predictions.
The subjective evaluations used in collaborative filtering may be implicit
rather than explicit. Read Wear and Edit Wear guides users based on other
users' interactions with an artifact [HHWM92a]. This is done by
associating the history of their use with computer documents. This is
called the ``wear'' of an article/object. Objects with more wear are the
more commonly used articles. Further, the wear acts as an indicator of the
content of the article. PHOAKS another system based on Usenet news articles uses
recommendations. This system searches newsgroups for any mention of web
pages and then uses that information for assisting users on an information
hunt [THA97]. PHOAKS provides a ranked list of articles where the
highest ranked articles are predicted to be the most preferred.
The user modeling community has spawned a range of recommendation systems
which use information about a user to assign that user to one of a finite
set of hand-built, predefined user classes or stereotypes. Based
on the stereotype that a user belongs to, the system then makes
recommendations to the user. For example, [Ric79] recommends
novels to users based on a stereotype classification.
The Grouplens [RIS94] system applies social information filtering to
the personalized selection of NetNews. Grouplens employs Pearson's r
correlation coefficient (a measure of the inherent strength of
the relationship between two sets of values) to determine the similarity between
users. The GroupLens news clients also monitor how long users spend reading each
article to get an implicit rating reflecting how much a user likes an article.
Finally, some commercial packages exist that make recommendations to users.
An example is Movie Select, a movie recommendation software package
by Paramount Interactive Inc. Some of the other movie recommendation systems
are Movie Critic, moviefinder and Morse. These
systems collect correlations between different items and use these to make
recommendations. Another system that
makes recommendations is the Sepia Video Guide by Sepia Technologies Inc.
Bostondine, another recommendation system by Hubnet Communication Ltd.
recommends restaurants in Boston that fit a user's tastes. Firefly and
NetShepard Rating Services have tools for rating and filtering Internet content.
Some ``customized newspapers'' developed by using cognitive filtering techniques are
LA Times, London Times, CRAYON etc. An ongoing MQP at WPI is
building a system to develop an on-line newspaper (Tango) using social filtering
techniques [MSNM99].
Economic filtering techniques select articles based on the costs and benefits
of producing and reading them. For example, Malone argues that mass mailings
have a low production cost per addressee and should therefore be given lower
priority [MGT87]. Applying this idea to Usenet news, a news
client might filter out
articles that had been cross-posted to several newsgroups. More complicated
schemes could provide payments (in real money or reputation points) to
readers to consider articles and payments to producers based on how much the
readers liked the articles.
Stodolsky has proposed a scheme that combines social and economic filtering
techniques [She94]. He proposes on-line publications where the publication
decision ultimately rests with the author. During a preliminary publication
period, other readers may post ratings of the article. The author may then
withdraw the article, to avoid the cost to her reputation of publishing an
article that is disliked.
The Fab system is a hybrid of the cognitive and
social filtering techniques discussed above [BS97]. Fab maintains user
profiles based on content analysis and directly compares the profiles
to determine similar users for collaborative
recommendation. Users ``receive'' items both when they score highly against
their own profile or when they are highly rated by a user with a similar profile.
The Ringo system is similar to [BS97] except that during
a similarity assessment between users, the system selects profiles of users with
the highest correlation with an individual user [UP95]. The Ringo
system uses mean-squared difference (a measure of the variance of articles)
and the Pearson- R measure (a measure of the inherent strength of
the relationship between two sets of values) to determine similarity.
Another System [BHC98] also combines social and cognitive filtering
techniques by defining additional features about the articles (For e.g. some
features of a movie could be the the actors, directors, writers etc. of the movie).
These features along with the proportion of a retrieved set of documents that
are relevant (called precision) and the proportion of all relevant
documents retrieved (called recall) are then used to categorize the
articles by degree of likability for users. Correlations with actual users are
not used in this system.
[SKB99] use filtering agents (filterbots) that act like normal users in
a collaborative filtering system. These filterbots
return ratings on articles based on certain semantic information. This system
used filterbots that generated ratings depending on the length of the article, the correctness of spellings in the article etc.
The tech report by Microsoft Research compares the various collaborative filtering
techniques and performs an empirical analysis on the same [BHK].
Conventional information retrieval (IR) [SM83] is very closely related to
information filtering in that they both have the same goal of retrieving information
relevant to what a user wants while minimizing the amount of irrelevant information
retrieved [SM83, vR79]. Selective Dissemination of Information
(SDI), one of the original information retrieval systems, is similar
to most information filtering applications [PS79, HK70].
SDI was designed as an automatic way of keeping scientists informed of new documents
published in their areas of specialization. SDI maintained keyword based profiles
of users and used these profiles to match the keywords against new articles to
predict which of the articles would be most relevant to the scientist's interests.
Furthermore, research done in the field of evaluation of IR techniques
[SM83, ] can also be applied to information filtering systems.
A number of measures of evaluating IR techniques have been developed with the
best known being precision and recall described above. These measures can also
adequately evaluate the
effectiveness of most information filtering techniques.
Further, Belkin and Croft identify the primary differences between
information filtering and retrieval [BC92]. This will help researchers in
the area of information filtering to benefit from research in IR, by ``customizing''
the IR techniques for information filtering while keeping in mind the differences between
them. These differences mainly arise because user preferences in information filtering
typically represent long term interests while queries in IR represent a short term
interest that can be satisfied by performing the retrieval. Also, information filtering
is typically applied to streams of incoming data while in IR, changes to the
information source do not occur often and retrieval is not limited to new items in
the information source. Finally, filtering involves the process of ``removing'' data
from the stream while IR involves the process of ``finding'' information in that stream.
In pure cognitive filtering techniques, only a very limited analysis of the content
can be performed. Only certain aspects of the text can be evaluated and other
aspects like aesthetic quality of multimedia information, style of language of
text, other computer non-scannable information like the network factors
(e.g. loading time )are completely ignored. Also filtering of items that do not match a
profile effectively inhibits the user from being able to see articles on new topics
(outside her profile) thus narrowing the scope of articles she sees.
On the other hand, social filtering techniques suffer from ``first user'' problems.
A new article coming in cannot be recommended to a user until it has been read
by at least one
person. Also sparsity of coverage of ratings (in situations where the number of users is
very small compared to the volume of data) can lead to inaccurate recommendations.
Finally, users with tastes dissimilar to other users are ``punished'' as there will
be very few users having a high correlation with such users. These can lead to
filtering systems that are unable to give a prediction or filtering systems that are
highly inaccurate.
We build upon past work in social and cognitive filtering techniques to combine the
advantages of both.We shall make improvements to the social filtering techniques to
minimize the effect of the above problems. We shall also integrate them with the
cognitive filtering techniques to minimize some of the problems outlined above.
We shall later propose techniques for the same.
We develop an algorithm to compute predictions that are more accurate
(closer to the rating the user would give the movie) than those given
by current algorithms. In this chapter we describe the basis algorithm,
describe the general design and setup for experiments to evaluate our
algorithms and explain our incremental improvements.
Although there is an increasingly strong demand for collaborative
filtering techniques, only a few different algorithms have been proposed
in the literature thus far [RIS94], [FD92],
[MGT87], [Mal94], [Suc94],
[BS97], [UP95]. Furthermore, most of these algorithms are
based on simple predictive techniques that use a measure of agreement
between users in order to make predictions. Like these previous
researchers, we consider a collaborative filtering algorithm that uses
a weighted average to compute predictions.
We choose these algorithms not only because they constitute a large
portion of the algorithms (including those used in commercial products)
but also because they intuitively generate predictions
for users based on the similarity between the interest profile
of that user and those of other users. These algorithms
compute the similarities (correlations) between user profiles or
compute correlations between users by looking at their history of
agreement over articles rated in common.
The basis algorithm defines correlation as a measure of the
degree of like-mindedness between pairs of users. We define likability
as a measure of how much the user will like/dislike the movie.
It is the amount by which her rating would be above or below her
mean. The mean, here, is an average over all the user's ratings.
It gives an indication of how ``stringently'' or
``leniently'' the user rates items. The basis algorithm uses
the Pearson's correlation coefficient to make full use of ratings between
users that have different rating systems by adding the likability
to the average rating the user gives her items to predict a rating for
that particular user. For example, user A may rate all items between
one to three where one is bad, two is average and three good while user B
may rate all items between three and five where three is bad, four average
and a five good. The algorithm adds the likability to the average of
user A (two in this example) to predict a rating for user A.
The general formula to compute the likability for an article for a
user by the basis algorithm is:
is the correlation of user i with the user for whom the
prediction is being computed. represents the rating submitted by
user i for the article for which the prediction is being computed.
is the average rating (the average of all the ratings for all
articles given by the user) for user i. is the total
number of users in the system that have some correlation with user .
These users are those whose ratings are used in the calculation of the
prediction for user .
Consider an example to demonstrate how the formula is used
to compute the prediction for an article for a user, X.
The following table gives the ratings for an
article by two users and their individual correlations with the user
X. We assume that the mean rating for the user X
is also known and equals 3 in this example.
User A
User B
Correlation
Mean for user X,
The prediction will be computed as:
Our basis algorithm considers ratings given by all the users for a
particular article in order to calculate a prediction. This includes
those users who have very low correlation between them. A Pearson's
correlation coefficient in the range is
considered to be a low correlation between users. Similarly
or is considered
a moderate correlation and and
is considered a high correlation between any two
users. Statistically, there is very little certainty that the ratings
of users with low correlation between them follow either a pattern of
similarity or dissimilarity. This suggests that the rating of such
users then not be allowed to have a bearing on the calculation of
the prediction. A contribution of this thesis is to improve the accuracy
of the basis algorithm by implementing a threshold on the correlation
such that only users with a correlation above the threshold will be able
to affect the prediction calculated by the system.
We can also see that the basis algorithm can produce inaccurate results
if the number of users whose ratings are considered are below a
certain minimum. As an example, consider the case where two users A
and B agree on most things except one topic. We would ideally not
like to consider just user B's opinion to compute a prediction for
user A for that particular topic (this is not handled by our basis
algorithm). On the other hand, if there are a hundred users (including
user B) who think like user A, then the rating of user B for that
particular topic would not adversely affect the prediction as the
rating of user B contributes a much smaller portion towards the
computation of the prediction.
The history (number of
items/articles rated in common between two users) should influence
the prediction in some way. As an example, consider the scenario
where user B has watched a hundred movies in common with user A and
has always agreed with user A while user C has watched just one movie
in common with user A but has agreed on that one movie.
In this case we cannot really be sure about user A being in agreement
with user C on the next movie. In fact the more movies user A watches
in common with user C, and agrees, the greater the faith we have in
the opinion of user C. There should be some way to differentiate
between such users and give the rating of user B more weight than that
of user C. We improve the accuracy of the basis algorithm by implementing
thresholds on the history in common between two users.
In this section, we present experiments that evaluate our proposed
improvements. We shall first describe the general experimental design.
We focus on the techniques we use to calculate correlations between
users and to compute a prediction for a particular article for a user.
We then describe the experimental setup for our improvements focusing
on how we compute the accuracy of a prediction.
The design for our experiments on the improvements
to the basis algorithm will comprise of off-line experiments.
This means that we do not perform these experiments on real users
using a live system but instead perform these experiments
on both data simulated by us and on data from previous collaborative
filtering experiments. The simulated data consists of both random and
pseudo-random data sets generated by us that simulate the ratings
provided by users in a real system.
The off-line experiments mainly consist of experiments on the data
from the EachMovie
collaborative filtering service. The EachMovie service was part of a
research project at the Systems Research Center of Digital Equipment
Corporation. The service was available for 18 months from February 1996
to September 1997. During that time the database grew to a fairly
large size, containing ratings from 72,916 users for 1,628 movies. User
ratings were recorded on a numerical six point scale. The data set is
publicly available and can be obtained from the Digital Equipment
Corporation (now Compaq).
As a part of the off-line design we maintain separate files
which store the ratings for different movies given by a
user and the correlations between all pairs of users in
the system. The ratings for the movies are extracted from
the EachMovie data set. These ratings are
stored as a matrix of users with ratings in a text file and
are later used to generate
correlations between users. The correlations between
users are generated as Pearson's correlation coefficients.
The system then uses these ratings and correlations and calculates
the prediction for every movie for every user. The predictions are
calculated using the formulae described in our individual improvements.
This is done by ``pulling out'' the rating for the
movie in question for a user. This means that when the system calculates
the prediction for that movie for the user, it ``ignores'' the rating
value for that specific instance from the matrix, thus simulating a
condition where the user has not watched the movie earlier and therefore
has given no rating for it. The prediction is then compared with the
actual rating for the movie in question for that user (the value
that was ``pulled out'' from the matrix during the computation of
the prediction) to give an indication of the accuracy of the
prediction. We describe this process in detail in the
next section covering the experimental setup. This process is carried
out for every movie for every user in the data set (for every point in
the generated matrix) to get the average accuracy of the prediction for
the data set.
We conduct similar experiments on random and pseudo random data.
For these experiments, we generate random/pseudo random data to represent the
ratings submitted by users for movies. All the other steps are the same as
those carried out for the off-line experiments on the EachMovie data.
The accuracy of a prediction can be measured by determining the number and
severity of errors. An error is the difference between the rating
prediction supplied by the system and the rating given by the
user. We test our algorithms by checking the variance and percentage
of errors produced by our algorithm.
An error is serious if the difference in the predicted
rating and that given by the user after rating the item is very
large while an error is trivial if the predicted rating value and
the actual rating given by the user varies not more than one level
so that rounding the prediction to the nearest level would not lead
to any recognizable error by the user. The trivial errors are therefore
a function of both the user interface used by the system and the scale of
the ratings. If the acceptable range of ratings is the list
of positive numbers between one to ten then an error of 0.3 for example
might not get noticed by the user as the prediction will get truncated
to the nearest integer. Consider the case where the rating given by a user
was 5. If the system computed the prediction as a 4.7 (so that the error
is 0.3) but rounded that off to 5 before showing it to the user then the
user would not even notice an error if the prediction was shown as a
number! On the other hand, if the user interface used a scroll bar to
indicate the prediction then the error might have been more noticeable.
As a second example, consider the situation where the system allows all
positive numbers between one and hundred as valid ratings. In this case
an error of 0.3 by the system would be less noticeable even on the
scrollbar user interface! We use a 10 point scale
to give ratings and predictions with all integers between 1 and 10 as valid
ratings (or predictions).
A `good prediction' will have low deviation of the
prediction from the actual rating. The metrics that we will use to measure
the accuracy of our algorithms include the following:
Mean Absolute Error :
Also called the arithmetic mean, mean absolute error is defined
as the sum of measures observed divided by the number of observations.
The lower the mean absolute error, the better the algorithm.
For our experiments, we compute the mean absolute error between the
rating given by the user and the prediction computed by the system.
Standard deviation:
The standard deviation is defined as the square root of the average
squared deviation from the mean. This is a measure of how consistently
accurate the algorithm is. For our experiments we compute the standard
deviation between the mean error for the data set and the error computed
for each individual prediction.
The basis algorithm computes a prediction by using the ratings
submitted by all the users of the system for the article in
question. This includes the ratings submitted by users who have a
low correlation with the user in question. This can lead to to
inaccuracies in the prediction if the number of users with a low
correlation increases or is more than the number
of users with a high correlation with the user in question. The
positive effect of the rating of like-minded users on the
prediction will be negated (or overshadowed) by the ratings of
users with low correlation with the user in question.
As an example, consider the case where user A has a high
correlation (equal to 0.8) with user B but a low correlation
(equal to 0.3) with users C, D and E. If user B gives a rating of 10
(on a scale of 1 to 10)
for an article and users C, D and E give a rating of 2, 4
and 2 respectively then the prediction computed by taking
all the users into consideration will be 5.47 which is closer
to 4 than to 10. Intuition suggests that since
user A generally agrees with user B than with the other users,
hence the prediction for user A should reflect the rating given by
user B more than the ratings given by the other users.
Another potential problem with using the ratings of all the users
is that there is an increase in the computation time which is
not justified by an equivalent increase in accuracy. Considering
the ratings of all the users (irrespective
of their correlation with the user in question) increases the
computation time exponentially with an increase in the number
of users. At the same time, this increase in computation time is
not justified by a corresponding increase in the accuracy of the
prediction. In fact, as we can see from the example above, the
accuracy can potentially drop!
To address this problem, we implement thresholds on the
correlations with users that are to be considered. For example,
if we had only taken the ratings of users above a certain threshold
(say 0.5) then we would have been guaranteed a prediction that
was closer to user B than to the other users. We
consider only those users that have a high correlation with the
user in question thus reducing the margin of error.
The advantage with this technique is that users with lower correlation
do not unduly affect the rating prediction and the prediction is based only
on those users who show either a high degree of agreement or disagreement.
The specific implementation of this improvement is as follows:
Find the number of users who have a correlation greater than the
threshold with the user in question.
For all such users, apply the basis algorithm described in section
3.1
We carried out off-line experiments on data extracted from the EachMovie
database [EM97]. Data sets were created by extracting the ratings
submitted by a subsection of the users on various movies. In order
to obtain a broad range of correlations between users. These ratings
were then stored as matrices with each element in the matrix
(dataset) representing the rating submitted by a user for a particular
movie, . We generated the prediction for every user for
every movie. This was done by ignoring the element (rating) in
the matrix for that particular user and movie. We then
considered the ratings submitted by other users for the movie
in question. We note that for this improvement we only considered
users who have a correlation above the threshold with the user
in question. We compared the prediction computed as above
with the rating (extracted from the EachMovie data) that
the user gave for the movie. We repeated this same procedure for
every user and movie (for every data element in the matrix data set).
We computed the average absolute inaccuracy
(absolute difference between the generated rating and its computed
prediction) for the whole data set. This is the average inaccuracy
of the data set for that particular value of the correlation threshold.
We then repeated the same procedure for different values of the
correlation threshold.
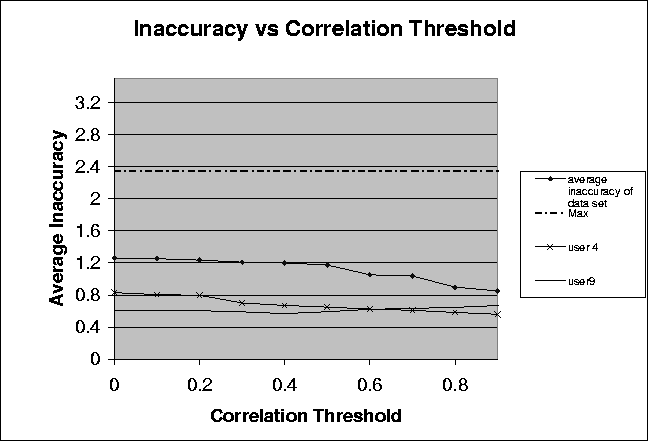
Figure:Plot showing the relationship between the average inaccuracy and the correlation threshold for data from the EachMovie Data. This dataset consists of the ratings of 58 users and 125 movies. Average inaccuracy is an average of the differences between the rating and the prediction for every pair of users and movies in the data set.
Figure 3.1 illustrates the results from our
experiments on a data set consisting of ratings submitted
by 58 users for 125 movies.
The ratings in the data set are extracted from the EachMovie data.
The ratings submitted were on a scale of 1 to ten.
The line labeled Max shows the average of the of all
the users in the data set. This is computed by
taking the average of the inaccuracies in the prediction returned for all the
users if the prediction returned was the mean rating of the user.
We plot this as this is the prediction returned for the user if no user in
the data set has a correlation higher than the threshold with the user
in question.
The line labeled average inaccuracy of data set shows the average
inaccuracy for the data set for the corresponding correlation
threshold value. The average inaccuracy was
calculated by taking the average of inaccuracies in all the predictions
computed by the system for every pair of users and ratings.
The lines labeled user1 and user9 show the average inaccuracy in
the predictions for individual users. This is computed by taking the
average of the inaccuracies in the predictions for all the movies
for that particular user.
We can see from the graph that the mean rating of the data set
(Max) is always higher than the average inaccuracy of
the data set for all values of the threshold.
As discussed earlier, we know that the mean is the prediction returned
by the system when the number of users with a correlation above the threshold
with the user in question is zero. This means that the prediction returns a
mean when the ratings of other users are not considered at all (collaborative
filtering techniques are not applied). This value is above
the average inaccuracy of the data set even when no thresholds are applied.
Using collaborative filtering techniques, therefore,
is better than just returning the mean as the prediction.
The curve labeled average inaccuracy of data set shows the
average inaccuracy of the data set for different correlation
thresholds. The average inaccuracy of the data set
drops with increasing values of correlation thresholds. This is because
at each correlation threshold, the rating of the users who have a value
less than the correlation threshold are not considered. We are thus
increasingly considering only those users whom we agree with the most.
This implies that the application of correlation thresholds leads to
increased accuracy of the predictions.
Lines labeled user1 and user9 show the average inaccuracies for
two different users in the data sets. We can see that the accuracy of the
prediction for the user in
Line user1 benefits all the time from the application of
correlation thresholds.
This implies that the correlation threshold of 1.0 (considering only those
users whom the user in line 3 always agrees with) is the best choice.
Line user9, on the other hand, shows that the average inaccuracy
for that user decreases upto a certain value of the threshold but then
increases if the correlation threshold value is further increased.
Though application of correlation thresholds is beneficial for the user
in line user9, the value of the best threshold for the user in
line user9 is not the same as that for the user in line
user1 (which is the same as the best threshold value for the
average inaccuracy of the complete data set). There is no correlation
threshold that works best for all the users in the data set. Correlation
thresholds should be different for different users to be able to compute
the best predictions. The best correlation threshold value is most likely
influenced by the number of users who are above this correlation threshold
value. In particular, the inaccuracy increases with increasing correlation
thresholds if the number of users who have a correlation above the threshold
value drops below a certain number. However, the number of users varies from
40 to 49 and is not the same for each individual user.
We also carried out off-line experiments on random data sets. We generated
random data sets as matrices by using a pseudo-random number
generator to generate the ratings submitted by users for different
movies.
We performed experiments similar to those on the EachMovie data. The
graph shown below illustrates the relationship of the inaccuracy of
the prediction and the correlation threshold value.
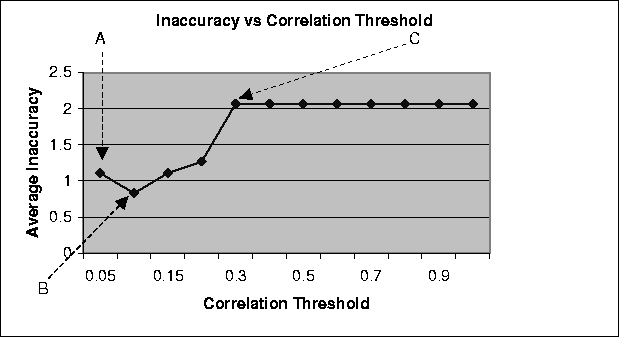
Figure:Plot showing the relationship between the average inaccuracy and the correlation threshold for a random data set consisting of 10 users and 100 movies. Average inaccuracy is an average of the differences between the rating and the prediction for every pair of users and movies in the data set.
Figure 3.2 illustrates the results from our
experiments on a data set consisting of ratings submitted
by 10 users for 100 movies. The ratings submitted were
on a scale of 1 to ten. The average inaccuracy plotted in the
graph is the average inaccuracy for the data set for the corresponding
correlation threshold value. The average inaccuracy was calculated by
taking the average of inaccuracies in all the predictions computed by
the system for every pair of users and ratings.
Point A on the curve shows the average inaccuracy
when there is no correlation threshold applied (correlation threshold
is 0.0). Point B on the graph shows the average inaccuracy when the
correlation threshold is 0.1. Point C shows a rise in the
inaccuracy when the correlation threshold is increased to 0.3.
Figure 3.3 also illustrates the relationship between the
average inaccuracy of the data set and the correlation threshold.
This graph illustrates the results of the same experiment (with correlation
thresholds) on a random data set with the same number of users but a
greater number of movies (five times the number of movies as in the first
graph).
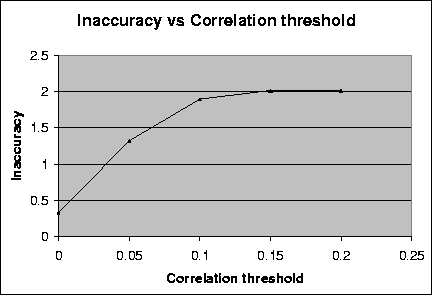
Figure:Plot showing the relationship between the average inaccuracy and the correlation threshold for a random data set consisting of 10 users and 500 movies. Average inaccuracy is an average of the differences between the rating and the prediction for every pair of user and movie in the data set.
We can see from the above graphs that the use of random data to test for
collaborative filtering techniques is not very useful. The inherent randomness
of the data generated does not loan itself to computations of correlations
or the predictions made using the correlations. We make the following
general observations:
It is difficult to model real life data representing the
opinions of people on various topics using random data sets. We normally
expect people to have similar opinions on different movies/articles on the same
topics. This behavior is difficult to reproduce in random data.
It is also very difficult to ``randomly'' generate two sets of
numbers such that the correlations between them remain almost the same or
to generate them such that the next pair of number in each set models the
correlation of the two sets up to that time.
Finally, two sets of data generated randomly have almost no correlation,
so that if these sets are used to represent ratings submitted by users than
the data set would consist of ``users'' such that all the users have a
very low correlation with each other.
We shall henceforth perform all our off-line tests only
on data from the EachMovie data set [EM97].
Typical collaborative filtering algorithms also use the ratings
submitted by users who have a low history with the user in
question. This means that the algorithms also consider the
ratings of users who have rated a low number of items in common
with the user for whom the prediction is being calculated.
This can lead to inaccuracies in the prediction
computed by the system if the number of users with a lower
history with the user in question increases or is more than
the number of users with a high history with the user in question.
There is no statistical basis for a prediction if the history of
agreement is low. For example 2 movies watched in common and liked
by both users does not guarantee or even strongly indicate that the
two users would agree on the next movie. A prediction based on the
opinions of users with low history is likely to be inaccurate.
The positive effect of the rating of users with a high history on
the prediction could be negated by the ratings of users with low
history with the user in question.
As an example, consider the case where user A has a high
history (two thousand movies watched in common) with user B but a low
history (two movies watched in common) with users C, D and E.
Assume also, for the example, that user A has the same correlation with
all the users such that user A has a correlation of 1.0 with users
B, C, D and E. If user B gives a rating of 10 (on a
scale of 1 to 10) for an movie and users C, D and E give a
rating of 2, 4 and 2 respectively then the prediction computed by taking
all the users into consideration will be closer to 4 than to 10. Since
user A has agreed all the time with user B for a range of two thousand
movies it is more logical to say that user A and user B think alike
and so the prediction for user A should be closer to the rating given
by user B. On the other hand, we can see that since users C, D and E
have not watched many movies in common with user A, a high correlation
with user A does not always guarantee a proven history of agreement
between user A and users C, D and E. We therefore cannot really
justify making a strong prediction based on their ratings.
We tune our basis algorithm such that the weighted
average formula for the computation of the prediction is applied only
to users who have rated more items in common than the history threshold.
We implement history thresholds such that we consider the
correlation and the rating given by each user only for users who have the
number of items rated in common greater than the history threshold
imposed by the system. We carry out our experiments on different values of
history thresholds.
In our example, if we had only taken the ratings of users above a certain
threshold (say 50 movies watched in common) then we would have been
guaranteed a prediction that was closer to user B than to the other users.
We consider only those users that have a high
history with the user in question thus reducing the margin of error.
The advantage with this technique is that users with
lower history do not unduly affect the rating prediction and the
prediction is based only on those users who show either a proven
degree of agreement or disagreement.
The specific implementation of this improvement is as follows:
Find the number of users who have a history greater than the
threshold with the user in question.
For all such users, apply the basis algorithm described in section
3.1
We carried out off-line experiments on data extracted from the
EachMovie database
by extracting the ratings for various movies for a number of users
such that each element in the matrix (dataset) represented the rating
submitted by a particular user for a particular movie. We note that
since the EachMovie database is very sparse (with a density of
ratings of only about 2 percent) we had to limit our choice of
users and movies that we used in the data set such that the
users submitting more ratings and
movies for which more ratings had been submitted were selected
over others. This was done to ensure that most users had at least
two movies in common with some other user. (This is necessary
for the system to be able to compute a correlation between the two users).
We also had to ensure that the users and movies were selected
such that at least some users had a history in common (movies watched
in common with each other) greater than the history threshold value
so that the system could compute the prediction for all the
history thresholds in the experiments.
We generated the prediction for every user for
every movie that the user had watched and submitted a rating for.
We performed experiments similar to those for the correlation thresholds
improvement.
The graph shown below illustrates the
relationship of the inaccuracy of the prediction and the
number of users in the data set for data extracted from the
EachMovie database [EM97].
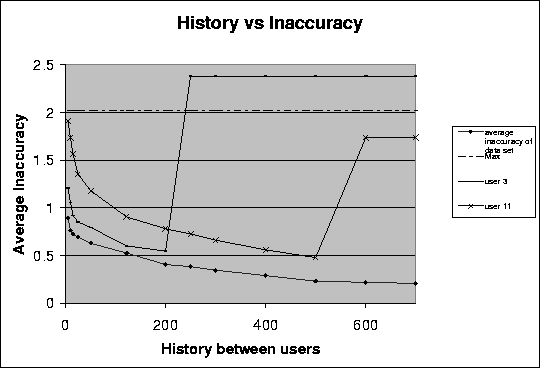
Figure:Average inaccuracy and the history in common between any two users. The number of users is kept constant at 125. Average inaccuracy is an average of the differences between the rating and the prediction for every pair of users and movies in the data set.
Figure 3.4 illustrates the results from our
experiments on a data set consisting of ratings submitted
by fifty eight users for six hundred movies.
The ratings in the data set are extracted from the EachMovie data.
The ratings submitted were on a scale of 1 to ten.
The line labeled Max shows the average of the of the data set.
This is computed by taking the average of the inaccuracies in the prediction
if the prediction returned was the same as the user's mean rating value.
We plot this as this is the prediction returned for the user if no user in
the data set has a history in common higher than threshold with the user
in question.
Line average inaccuracy of data set shows the average
inaccuracy for the data set for the corresponding history threshold value.
The average inaccuracy was
calculated by taking the average of inaccuracies in all the predictions
computed by the system for every pair of users and ratings.
Lines user 3 and user 11 show the average inaccuracy in
the predictions for individual users. This is computed by taking the
average of the inaccuracies in the predictions for all the movies for
that particular user.
We can see from the graph that the mean rating of the data set
(Max) is always higher than the average inaccuracy of
the data set for all values of the threshold.
As discussed earlier, we know that the mean is the prediction returned
by the system when the number of users with a history in common above
the threshold with the user in question is zero. This means that the
prediction returns a mean when the ratings of other users are not
considered at all (collaborative filtering techniques are not applied).
The line labeled average inaccuracy of data set shows the
average inaccuracy of the data set for different history
thresholds. We can see that the average inaccuracy of the data set
drops with increasing values of history thresholds. This is because
at each correlation threshold, the rating of the users who have a value
less than the history threshold are not considered. We are thus
increasingly considering only those users whom we have watched the most
movies in common with. This implies that the application of history
thresholds lead to increased accuracy of the predictions.
Lines user 3 and user 11 show the average inaccuracies
for two different users in the data sets. We can see that the accuracy of
the prediction for the user in line user 3 benefits
from the application of correlation thresholds upto a certain value.
The history threshold of 200 (considering only those users with whom the
user in line user 3 has watched at least 200 movies
in common) results in the maximum accuracy. Line user 11, on
the other hand, shows
that the average inaccuracy for that user decreases upto a certain
value of the threshold but then increases if the history
threshold value is further increased. Though application of history
thresholds is beneficial for the user in line user 11, the
value of the best threshold for the user in line user 11 is not
the same as that for the user in line user 3.
There is, thus, no history threshold that works best for all
the users in the data set. The history thresholds, therefore, should
be different for different users to be able to compute the best predictions.
We plotted the average inaccuracy for other users as well and made similar
observations in the trends about the inaccuracy and the best history
thresholds for individual users.
We also observed that the optimum correlation threshold value depends on the
number of users who are above this history threshold value. In particular,
the inaccuracy increases with increasing correlation thresholds if the
number of users who have a history in common above the threshold value
dropped below a certain number. This number of users, however, is not
the same for all users and varies between 35 to 50.
As we mentioned earlier, we also believe that the ``strength'' of
predictions computed by considering users who have a low history
in common with the user in question would be low.
For example, consider a situation where user A and user B have watched
just two movies in common and have agreed on both. There is no
statistical justification in assuming that they will think alike on the
next they watch (i.e. the prediction is inherently weak).
On the other hand, if user A and user B had watched two thousand movies
in common and agreed on all then they are likely to agree on the
next movie they watch.
We have also discussed earlier that predictions computed by using
the ratings of users who have a low history also leads to predictions
that are not consistently accurate. The history
between users is not high enough to guarantee that the correlation
computed between these users is a true indication of their degree of
similarity or dissimilarity. We would thus assume that such predictions
would have a high standard deviation. (This has been discussed in more
detail earlier in section 3.2.2).
We perform analysis on the data from the above experiments to see the
effect of the history on the strength of the prediction. We compute the
standard deviation of the inaccuracies in the predictions. We then plot
the average inaccuracy of the data set and also plot graphs which are at
1 standard deviation distance from the average. (For normally distributed
data approximately 60 percent of the total predictions would lie in the
range within 1 standard deviation of the mean.
The graph shown below illustrates the
relationship of the inaccuracy as well as the standard deviation
of the inaccuracy of the prediction and the history in common
between the users in the data set for data extracted from the
EachMovie database.
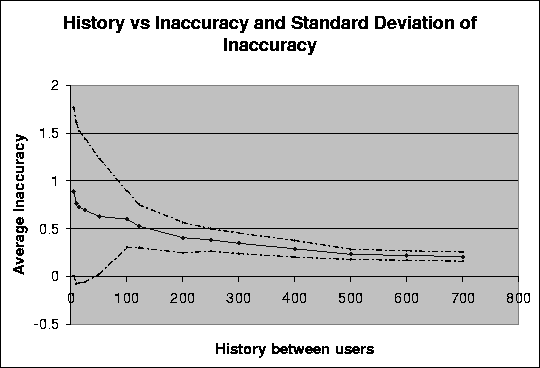
Figure:Plot showing the relationship between the average inaccuracy, the standard deviation of the average inaccuracy and the history in common between any two users in the data set for a data set consisting of ratings extracted from the EachMovie database. Average inaccuracy is an average of the differences between the rating and the prediction for every pair of user and movie in the data set.
We observe in figure 3.5 that the standard deviation is
really high for a history in common of five movies and then rapidly
drops with an increase in the history in common between users.
This supports our earlier conclusion that an increase in the history
in common between any two users will lead to predictions that are
not just more accurate but also more consistently accurate.
A potential problem with the basis algorithm is that the rating
prediction computed by the system for a particular article for
a user could be outside the valid range for the rating. This
means that if the ratings given by the user are on a scale of
1 to ten, then the prediction could be either greater than
10 or less than 1 for some cases. This can
potentially lead to problems of interpretation
of a prediction. For example, if the system sometimes returns a
prediction of 12 (while the allowed range of valid ratings
is between 1 to ten) it will be forced to represent this
prediction of 12 as a 10 as that is the maximum possible
in the range. This leads to questions about the confidence a
user can place in a prediction computed by the collaborative
filtering system as she has no guarantee that if a prediction of
12 should be taken as a 10 then a prediction of 10 for
example should still be taken as a 10 (since this is in the
valid range and the system does not have to ``round'' it off
as in the previous case) and not as a 8.
We try and reduce the effects of this problem by
normalizing the likability so that the final rating
prediction is always between the minimum
and maximum rating values. This allows us to convert
the prediction value calculated into an accurate
measure of the likability of a movie.
The specific improvement is as follows:
Calculate the likability for user x using the formula in the
basis algorithm:
Rating =
let Max rating allowed= and minimum rating allowed =
If (
Normalize (maximum likability - ) to ( -
)
If (
Normalize (-minimum likability ) to ( - )
Final rating prediction = mean + normalized value
We carried out various experiments using both random and pseudo-random
data sets and the data from the EachMovie database. We also carried out
various tests and computed the predictions
on all combinations of movies and users for varying data sets.
These predictions were computed for data sets of varying sizes and shapes
(ratio between number of users and movies watched by users in a data set).
We found, however, that though such a situation (of obtaining predictions
above or below the valid range of ratings) can be theoretically
possible, it never happened in all our tests. We conclude that this
``improvement'' need not be implemented with the intent of improving the
quality of the prediction.
In this chapter, we describe the motivation for an integration of
content and collaborative filtering techniques. We also describe
the content filtering algorithm and its various pieces. We implement
content based filtering using a keyword matching technique. In the
following sub-sections we shall talk about the techniques
we use for key-word generation and matching and their application
to the user profile in our content-based filter.
The results from figure 3.3 suggest that
collaborative filtering by itself cannot always guarantee a good
prediction. On the contrary, the inaccuracy can increase if the number
of people who have a correlation with the user in question is very low.
In particular, figures 3.1, 3.2 and
3.3 suggest that correlation thresholds selected for
a data set produce more accurate predictions as long as the
number of users which have a correlation above this threshold with
the user in question is above a certain limit.
We performed experiments to observe the effect of the number of users
on the average inaccuracy of a data set.
We have seen earlier in figures 3.2 and 3.3 that
the average inaccuracy of the data set (when correlation threshold is zero)
decreases when there is a corresponding increase in the number of users.
We also note that this was not observed for higher correlations as the
number of users above higher correlation thresholds in the second data set
were very few. This lack of enough users above a correlation threshold
was unavoidable due to the nature of randomly generated data sets.
We therefore used the ratings from the EachMovie data set to perform our
experiments [EM97]. We also note, that for the purpose of our experiments
on user thresholds we kept the number of articles in the data set constant.
The specific implementation of this experiment is as follows:
Extract the ratings from the EachMovie data set for a small
number of users (we start our experiments with five users in the data set).
For all such users, apply the base algorithm described in
section 3.1.
Calculate the average inaccuracy of the data set.
Increase the number of users and perform the experiment
again.
We used data from the EachMovie data set and performed experiments
similar to those defined in chapter 3.
These experiments were then repeated for a similar data
set extracted from the EachMovie database but with increasing number
of users in the data set, keeping the articles in all the data
sets constant. We carried out experiments with the number of
users varying from five to six hundred.
The graph shown in figure 4.1 illustrates the
relationship of the inaccuracy of the prediction and the
number of users in the data set for data extracted from the
EachMovie database.
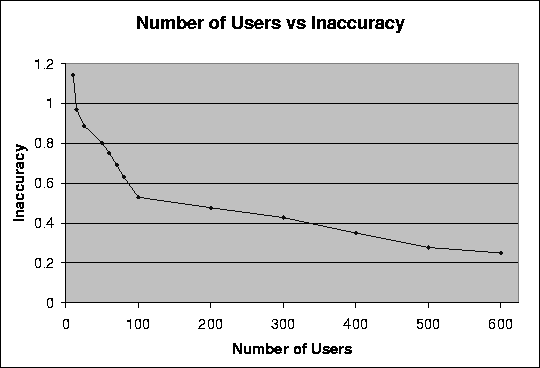
Figure:Plot showing the relationship between the average inaccuracy and the number of users in the data set for a data set consisting of ratings extracted from the EachMovie database. The number of articles is kept constant at 125. Average inaccuracy is an average of the differences between the rating and the prediction for every pair of users and movies in the data set.
The EachMovie data has been described in more detail earlier in
section 3.3.1.
We observe in figure 4.1 that the inaccuracy drops with an
increase in the number of users. We also note that the inaccuracy
in the data set drops more rapidly in the first part of the graph when
the number of users increases from 5 to a 100. As we can see there is a
rapid decrease in the inaccuracy in the first part of the graph (till
the number of users equals 100). We believe this is due to the fact
that in the beginning the number of users is very few and
therefore there is a greater chance of error if the users
have a low correlation. This error could also occur even if they have a
generally high correlation but if they disagree on that topic with the
user in question. As there are very few users in the system, the
contribution of each user's rating towards the final computed prediction
is high and therefore can lead to a higher inaccuracy in the prediction.
We note that the the decrease in inaccuracy is much slower in the interval
when the number of users increases from 100 to 600.
We believe this is because of two reasons. First, the number of users
is large and so the prediction is fairly accurate. A further
increase in the number of users (from 100 to 600) does not significantly
improve the prediction. Second, as the number
of users in the data sets is large, the contribution
that a single user makes to the prediction is small. So cases where two
users have a high aggregate correlation but disagree on the subject of
the article in question does not lead to significant inaccuracies in
the prediction. The negative effect of such cases on the prediction is
reduced as the number of users is large and therefore any one user does
not significantly influence the prediction.
Figure 4.1 shows that collaborative filtering works better
on data sets with larger numbers of users. It also shows that when
the number of users in the data set is small the inaccuracy in the
prediction computed by the collaborative filtering techniques is higher.
We have just seen that one disadvantage with pure collaborative filtering
techniques is that predictions computed can be very inaccurate in the
beginning stages when the number of users and articles rated by users is low.
In some cases, the collaborative filtering systems may not even be able to compute
the prediction. A user has to have rated at least two articles in common with
another user for the system to be able to compute a correlation between them. In
the beginning stages of the collaborative filtering system, the number of articles
rated in common between any two pair of users is very low (Collaborative filtering
systems can be very sparsely populated). This can lead to situations where the
system may not be able to compute a prediction at all or will compute the prediction
based on the ratings of very few users making it highly prone to inaccuracies.
Also even if two users have a high correlation between them, they may not agree on
particular topics. A user may want to see items on certain topics irrespective of
the opinions of other users.
All the above observation suggest that pure collaborative filtering techniques
are not sufficient and there is a need to make them more accurate. We suggest
using content based filtering techniques in conjunction with pure
collaborative filtering techniques to improve them.
In the following sections, we shall describe the content filtering
algorithm and the integration of content and collaborative filtering
techniques proposed by us.
We implement the content based algorithm using a keyword matching technique that
relies on the significant words of the article and the user specified profile.
We shall, therefore, first briefly describe the format of the user's profile
required for the calculation of the content based prediction.
The user's profile is setup as follows. Each profile is divided into
sections that the information source is divided into. These sections
can ideally correspond to newsgroups if the prediction is for a Usenet
News system, to the various sections that a newspaper is divided into or
the various categories that web sites are divided into (for example the
various categories which the users of AOL can choose to explore when they
first log in). We develop a system that uses newspaper articles to perform
experiments on the content filtering algorithm. We shall discuss the
specific design of this system in later sections. We divide the profile
of users into sections of a newspaper as
we use a collaborative filtering system for a newspaper to test our
integration of collaborative filtering with content based filtering. In this case for example,
each profile will have sections like sports, world news etc. A user
can choose to be shown articles belonging to particular sections.
This is done by clicking on the checkbox for that particular section.
For example, if a user chooses sports but does not choose world news
then this implies that the user wants the system to compute higher
predictions for articles under the sports section and not to articles
under the world news section. In addition, a user can specify keywords
for any section. Articles containing these keywords get a higher weight
by the system. So if the user specifies basketball as a keyword in the
sports section then sports articles on basketball should be given
higher weight than other sports articles.
In addition to the profile setup by the user (also called the explicit
profile), each user also has a set of implicit keywords that the system
assigns. This list of keywords is populated by appending the
keywords of the articles that the user has given a higher rating to the
pre-existing list of implicit keywords. This list is a continuously
changing and growing list. For example, if the user has given a rating of
10 (on a scale of 1 to 10) then all the keywords extracted from the article
will be appended to the user's list of implicit keywords. This list,
therefore, acts as an indicator of what the user has liked in the past.
We can see from the above description that even if the user specifies no
keywords but selects a section, the system should still be able to
use that information to give some feedback on how well he would like a
particular article. Specifying keywords can lead
to a stronger and more confident prediction on the likability of the
articles. It would thus be more beneficial if the articles liked by the
user in the past can also be used by the system to give a higher rating
for articles that are similar (in our case, containing similar keywords)
to those which the user gave a higher rating. This becomes more significant
when we consider the fact that some users may not be able to give explicit
keywords to describe their choices.
This implies that the system should consist of three parts and then combine
them at the end. The three parts we refer to are:
Implement a matching function on the explicit profile and the
article keywords. We shall henceforth refer to this score as Me.
Implement a matching function on the user's list of implicit
keywords and the article keywords. We shall henceforth refer to this
score as Mi.
Compute a score depending on whether the user wants to see all the
articles in the section under which article in question appears. We shall
henceforth refer to this score as Mc
Until conclusively proven otherwise, we shall treat them all equally (we shall
assign equal weights to them during the computation of the content based score).
As mentioned earlier, we base our algorithm for content based filtering
on the technique of keyword matching to determine how close the article
matches the user's keywords. Since the aim of this research is just to
explore the effect of integrating content based filtering techniques
with pure collaborative filtering and to design a way to implement
the same, we feel it is sufficient to implement a simple content
based filtering algorithm like keyword matching.
We base our algorithm on the technique proposed by Luhn which
states that the frequency of occurrence of words in an article
furnishes a useful measurement of word significance [Luh58].
Let f be the occurrence of various words in a text
and r their rank order, that is, the order of their
frequency of occurrence. A plot relating f and r
yields a curve similar to the hyperbolic in figure 4.2.
This is in fact a curve demonstrating Zipf's Law [Zip49] which
states that the product of the frequency of words and the rank order
is approximately constant. Zipf verified his law on American
Newspaper English. Luhn used this as a hypothesis to enable him to
specify two cut-offs, an upper and a lower (see figure 2.1), thus
excluding non-significant words. The words exceeding the upper cut-off
are considered to be common and those below the lower cut-off rare,
and therefore not contributing significantly to the content of the
article.
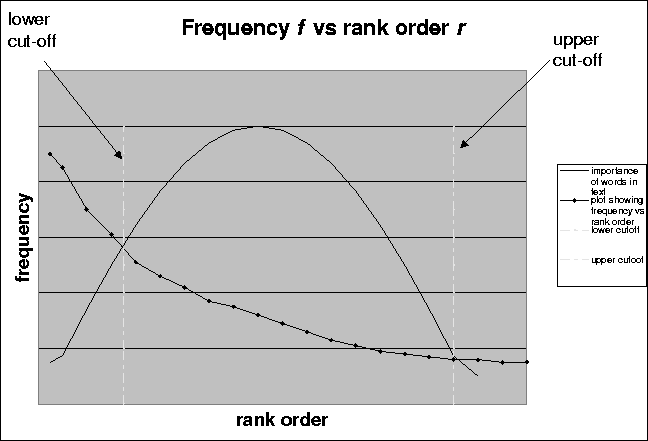
Figure:Plot showing the relationship of the frequency of a word in an article and its rank order determining its importance in the article.
Edmundson and Wyllys generalized Luhn's work by normalizing his
measurements with respect to the frequency and of occurrence of general
words in a text [HE61].
They thus devised a counting technique for finding significant
words. Consistent with this, they assumed that the resolving power of
significant words, by which he meant ability of words to discriminate
content, reached a peak at a rank order position half way between the
cut-offs and fell off from the peak in either direction reducing to
almost zero at the cut-offs. Luhn, though, gave no values of these
cut-offs. We suspect that this is because the cut-off values vary
with information domains and document/article types. For our purpose,
we shall fix these cut-offs for our experiments at one-fourth and
three-fourths of the rank order. We can then use the words between
these cut-offs as keywords for the article.
We note that just applying the above technique in a straightforward
manner to the words of an article can lead to errors.
Different forms of the same words (e.g. factual, facts, fact) are
considered as different words by the system during the determination of
frequency of occurrence. For example, the three forms of the word ``fact''
shown above are assigned a frequency of occurrence equal to one each
while in reality a frequency of occurrence equaling three should be
assigned for the word fact as the three words are simply
different forms of the words fact. We can see that to achieve this
something more needs to be added to our basic Luhn's technique.
Such a system needs to be able to detect equivalent stems (in our
example the stem for all the three words is fact) and use these stems
while implementing Luhn's technique.
We need to be able to extract the stems of different words and
consider two words with the same stem
as two occurrences of the same word for the sake of calculating
the frequency of occurrence. A standard approach to suffix-stripping
is to maintain an exhaustive list of suffixes and remove the
longest possible one. Unfortunately, context free removal leads
to a significant error rate. For example, we may want the suffix
ual removed from factual but not from the word
equal. To avoid erroneously removing suffixes, context
rules are devised so that a suffix will be removed only if the
the context is correct:
The length of remaining stem exceeds a given number; the
default in such a system is usually 2.
The stem-ending satisfies a certain condition, e.g. does not
end with q.
Many words, which are equivalent in the above sense, map to one
morphological form by removing their suffixes. Others, unfortunately, though
they are equivalent, do not (for example, absorbing and
absorption). Since there is no easy
way of making these fine distinctions, we put up with a certain
proportion of errors and assume that they will not significantly
degrade effectiveness. Experiments have shown that the error rate tends to be
the order of 5 percent [And71]. It has also been shown, that
using a slightly different approach to stemming [Lov73] also
produces errors of the same order of magnitude.
Once we have generated keywords for an article, we need to match
sets of article keywords with those in the user profile and
return a numeric indication of the closeness of the match of
the article for the user. We shall henceforth refer to it as
the Matching Function.
We need the matching function to compute the degree of match between the
article keywords and the keywords in the user's profile. Let D be the
set of keywords representing the document (extracted as explained above)
and Q be the set of keywords representing the users profile. We
use the Overlap Coefficient to measure the degree of
match. This coefficient, M, does not take into account the sizes of
D and Q. This is important as the number of article keywords could be
much larger than the keywords in the user's profile. Also the implicit
keywords for a user grow with time and can be much larger in size than the
users profile. In such cases it is important to use this technique as what we
need to check is not how many of the words in the two sets match, but
what percentage of the profile's words match. For example both users A and B
should get the same score if all the words in their profile are found in the article.
This should not change even if user A had specified only 2 words in the profile and
user B had specified 100.
This technique is a normalized version of the simple matching
coefficient. The formula to calculate the overlap coefficient is given below:
We now concisely describe the complete content based filtering algorithm.
To calculate the rating M for every article we
maintain a list of possible suffixes (for example, ion, ual, ate). We
shall henceforth refer to this list as the suffix list
For every new article in the system:
Retrieve the article text.
Strip of the suffixes of all the words in the article.
In case of two or more matching suffixes, strip of the longest
suffix. What remains are what are called stems of words (e.g.
fact out of factual).
Count the number of occurrences of each such stem.
Calculate the order of frequency of occurrence of the stems.
Formulate a list of keywords for the article by taking all the
words that fall in between the upper and lower cutoff points.
For every pair of articles and users:
If the user has not already rated the article:
Apply the Matching Function to get Me and
Mi. Let D be the set of keywords representing
the document (one extracted above), Q be the set of
keywords representing the users profile
(explicit profile) and R be the set of keywords
representing the users implicit profile. We apply the
Matching to D and Q to calculate Me and to
D and R to calculate Mi (Refer to
section 4.2.4 for a description of the
matching function).
Calculate Mc. If the section under which the
article falls is selected by the user then Mc equals
one, else Mc equal zero.
Calculate the content based score. The content
based score can be
computed by taking the weighted average of Me, Mi and Mc.
We shall give a weight of one-third for each of Mc, Me,
Mi as we consider all three to be equally important
When the user rates an article:
If the rating submitted is high (above 9) then add the
article keywords to the user's implicit profile. We do this as
a rating of 9 or above on a scale of one to ten means that the
user has really liked the article. As the article keywords
``define'' the article, we can use these keywords as a measure
of which keywords the user has liked in the past. We can then
use these to determine how much a user would like a new article.
After we calculate the predictions computed by the content based
filtering and collaborative filtering algorithms respectively, we
need to integrate these scores and return one number that is an
indication of how well the user would like the article. In this
section, we shall briefly describe the techniques we use to
integrate the content based and collaborative filtering predictions
into one aggregate prediction.
The content based predictions would be more accurate in cases where
the number of users or the history between users is low. The content
based predictions for particular users may also be more accurate
in general if the the number of users who are similar to the user in
question is low. So if user A and user B agreed on most issues except
one and the prediction for user A for an article
on that issue was based only on user B we can see that the prediction
made thus will not be accurate. On the other hand, if this prediction was
based on the opinions of many like-minded users the margin of error would
be much less. The content based score would also be more accurate on topics
where the user wants to see articles irrespective of the opinions of others.
Similarly there are cases where the collaborative filtering score should
be relied on more. This happens if the user has not specified enough
keywords in his profile. The collaborative filtering
score would also be more reliable for articles which have similar but not
the same words/topics described in the users profile. This is where the
user's past history of agreement with other users may help as these other
users may have the similar words in their profile and his agreement in the
past with other users would indicate that the article in question should get
a high rating.
Both the collaborative filtering and content based scores are important but
the extent of their importance towards the aggregate score (or
prediction) is very user-specific. We therefore propose a system where the
aggregate score is a weighted average of the collaborative filtering and
the content based scores. We also ensure that the weights attached to the
collaborative filtering and the content based score are different for
different users. These weights may also change over time to reflect the
change in a user's taste.
We integrate by giving an equal weight to both the collaborative filtering
and the content based scores for all the users. We then adjust these
weights according to the rating the user gives to every article. This is
done by comparing both the collaborative filtering and the content based
scores respectively to the rating given by the user for the article.
If the collaborative filtering score is closer to the rating given by the
user then we adjust the weights to give the collaborative filtering score a
higher weight than the content based score for future articles and vice
versa. The exact value by which the weights are adjusted depend on the
history. The formula for calculating this adjustment is specified in the
algorithm steps given below. This is an ongoing process making the system
self-learning. The increase or decrease in the previous weights is also a
function of the number of articles the user has already seen. This means that
a difference in the respective scores and the rating given by the user would
lead to a greater change in the weights if the user had seen just two articles
than if he had seen two hundred articles before the article in question.
Though such a system is slow-learning, as it adapts to changes in
a user's tastes slowly, it also ensures that the system does not change
drastically by ratings to articles that are unusual. For example, in cases
where a user wants to rely only on his profile for articles on basketball
and the article in question happens to be on basketball. In such a case,
even if the article has received a low collaborative filtering score we
don't want to change the weights by giving the content based score a very
high weight compared to the collaborative filtering as the collaborative
filtering score may be more accurate in general and only be bad for
articles on basketball.
We now concisely explain the complete algorithm to implement the above.
Integration Algorithm
Initialization:
final prediction = 0.5 * collaborative filtering score + 0.5 * content based filtering Score
Each time a user returns a rating for an article:
Check the collaborative filtering score, content based score and
the rating returned by the user for the article.
Check to see if the rating returned by the user is
closer to the content based score or the collaborative filtering score.
If the rating returned by the user is closer to the content based score:
new weight for content based score =
old weight of content based score + (0.1/number of messages seen by user)
if Number of articles rated by user100 then
new weight for content based score = old weight of content based score + 0.01
new weight for collaborative filtering score =
old Weight of collaborative filtering score - (0.1/number of messages seen by user)
if Number of articles rated by user100 then
new weight for collaborative filtering score = old weight of collaborative filtering score - 0.01
If the rating returned by user is closer to the collaborative filtering score:
new weight for collaborative filtering score =
old weight of collaborative filtering score + (0.1/number of messages seen by user)
if Number of articles rated by user100 then
new weight for collaborative filtering score = old weight of collaborative filtering score + (0.1/100)
new weight for content based score =
old Weight of content based score - (0.1/number of messages seen by user)
if Number of articles rated by user100 then
new weight for content based score = old weight of content based score - 0.01
We realize that to test a collaborative filtering algorithm that
also integrates content based filtering techniques, it is essential
to be able to get both the ratings of real users and the content of
the articles they rate. The EachMovie database has data only on the ratings
of the movies seen by the users. There is no information on what movie
the rating is for. Movies are represented only by article numbers and not
names. This makes it unusable for our experiments on the
integration of content and collaborative filtering experiments.
For this purpose we have built a system that gives the predictions
for newspaper articles for the users of an online newspaper [MSNM99].
This system allows the users to rate these articles and collects
the ratings given. The system allows users to maintain profiles
(containing sections and keywords for sections) specifying the users
interests (if any). The system then computes correlations between users
and gives predictions (for articles not yet rated by the user) based
on both the collaborative filtering base algorithm described in
section 3.1
and the content based filtering algorithm discussed earlier.
We will use this system to collect the ratings given by the user and
the predictions computed by the system to test the accuracy of
predictions.
In this section we first describe the general design
of our system. We shall focus on the techniques used to
calculate correlations between users and to compute a prediction
for a particular article for a user. We then describe the
experimental setup for our content based improvement focusing on
how we compute the ``accuracy''(or effectiveness) of a prediction.
The online experiments use real ratings submitted by real users
on a live system [MSNM99]. This system is designed to develop
a customized on-line newspaper for the Telegram and Gazette. This
uses a group of 18 users as a test-bed and collects ratings from
these real users as opposed to our off-line design. We shall
now briefly discuss the design of the system.
The system can be broadly divided into two parts: the front end and the
back end. The front end consists mainly of the graphical interface that
allows users to login and setup user profiles required for the content based
filtering. User's profiles are divided into the various sections of the
newspaper and users can choose to specify keywords that reflect their
interests. The front end is also responsible for showing users the predictions
for various articles and collecting the ratings given by users for the same.
These ratings are then uploaded to a database.
The back end of the system mainly consists of the database (where the ratings
and scores are stored) and the algorithms which compute both the correlation
between users and the prediction for an article. Correlations between users
are re-computed similar to the off-line design (i.e. the system uses
the Pearsons correlation coefficient
to calculate the correlations) once every day. The back end is also
responsible for converting the individual content based and collaborative
filtering scores to an integrated overall score using the algorithm
developed by us. This integrated prediction is then used as a measure
of likability of the article. The prediction is later compared with the
actual rating that the user give for the article. This is done to
get a measure of the accuracy of the prediction.
The front end shows a sorted list of articles in the order of the predictions
each time a user logs into the system.
We perform various analysis on the data collected by the online system.
The system computes the prediction for a user for a specific article.
We compare this with the actual rating
that the real user of the system gives to the article. We then
compute the difference between the prediction and the rating for
that article. This is done for all users for all articles.
This lets us compute not only the average inaccuracy (over all the
articles) for that user, but also the average inaccuracy
for the whole data set.
We then determine the accuracy of the prediction computed by the
system using the same measures of accuracy described in
section 3.2.2 for the off-line experiments
for our collaborative filtering improvements. We shall determine
the accuracy by the number and the severity of errors as defined
earlier in section 3.2.2. We shall use the
Mean Absolute Error for the same.
We carried out experiments on data collected from the live system developed
by us [MSNM99]. The data set comprised of 18 users. The articles in the data
set comprised of all the articles appearing in the newspaper for 2 months,
Ratings submitted by the users ranged from 1 to 10.
The graph in figure 4.3 shows the average inaccuracy in the
collaborative filtering scores for different users over time. We can see
that in the initial phases there is no value for some users as the system
is unable to even generate a collaborative filtering prediction for that particular
user in this time period. The system is unable to generate collaborative filtering
predictions for the user in the graph as the user does not have at least two
articles in common with any user. This means that the system cannot generate
a correlation between this user and any other user in the system. We also know
that our system can compute content based scores for every article for the user
as long as the user has either specified something in his profile or has rated
at least one article. The system cannot generate predictions
for only those cases where the article for which the prediction is being
generated is the first article a user is reading and the user has not
specified anything in his profile. In this case, the system can use neither
the implicit keywords nor the users profile to compute the content based score.
We can thus claim that the integration of content based techniques with pure
collaborative filtering techniques can ensure that the system can generate
predictions for almost all articles (except sometimes the first article)
for all the users.
Figure:Plot showing the average inaccuracy in the collaborative filtering score with time.
We also perform analysis on the whole data set to see the relative
inaccuracies of the pure collaborative filtering score, the content based
filtering score and a combination of the two. The graph in figure 4.4
shows the inaccuracy of the individual collaborative filtering and content filtering
scores as well as the integrated score (the prediction returned to the user by
the system).
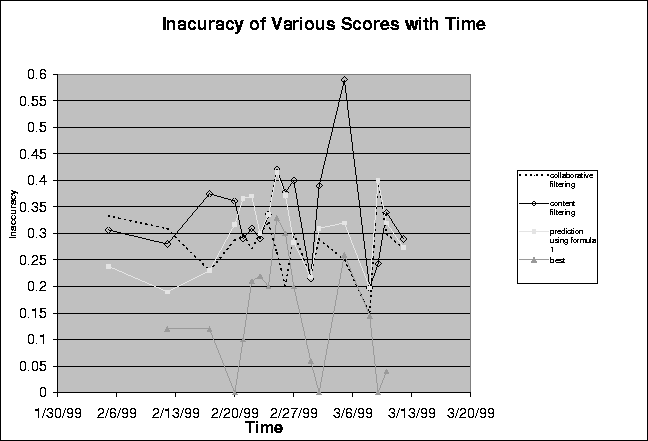
Figure:Plot showing the relationship between the inaccuracies in the content based filtering score, the collaborative filtering score and the integrated prediction. This dataset consists of the ratings of 18 users and all newspaper articles over 2 months. Percentage inaccuracy is an average of the percentage of inaccuracies in the prediction for every pair of users and movies in the data set.
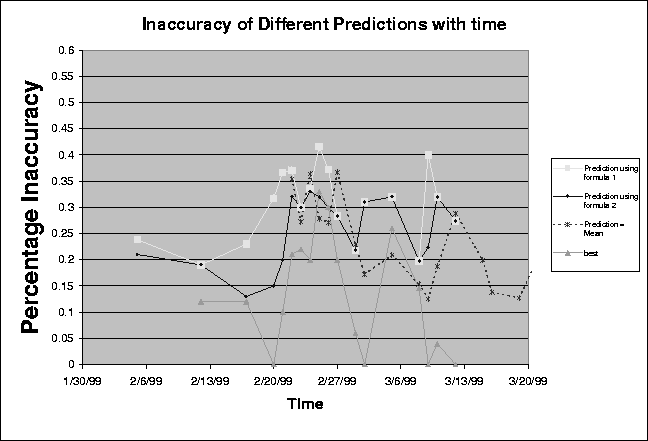
Figure:Plot showing the relationship between the inaccuracies in the predictions computed using different techniques. This dataset consists of the ratings of 18 users and all newspaper articles over 2 months. Percentage inaccuracy is an average of the percentage of inaccuracies in the prediction for every pair of users and movies in the data set.
We can see from figure 4.4 that the collaborative filtering
score is more inaccurate in the beginning. This as we mentioned earlier is because
of the the fact that the number of users who have a correlation with
the user in question is very few. We have also shown in chapter 3
that if the history in common between people
is low then the predictions generated by pure collaborative filtering
techniques are more inaccurate. The graph shows that the collaborative
filtering score becomes more accurate with time.
We can also see that the content based filtering score is generally more
accurate than the collaborative filtering score in the initial stages of
the graph. In some cases the collaborative filtering score cannot be
computed by the system at all. In such cases the content based score
can be returned to the user as the prediction. This ensures that the
system can compute a prediction for all users for most articles.
We also see from the graph that the integrated score (prediction)
in fact becomes more accurate than the collaborative filtering score in
the initial stages of the system because of the effect of content based
filtering. The integration of content based filtering techniques, thus,
helps improve the accuracy of the prediction.
Figure 4.4 also suggests that the integrated prediction
(the curve labeled prediction using formula 1) becomes more
inaccurate than the collaborative filtering score after a certain time
has elapsed. We have discussed earlier that the integrated prediction
is a weighted average of the content based and collaborative filtering
scores. We believe that this inaccuracy arises because the weights
assigned to the collaborative and content based predictions are inaccurate.
The content based score is generally more inaccurate than the
collaborative score in the later stages of the system and assigning it a
high weight will lead to more inaccuracy. The curve labeled best
shows the inaccuracy in the prediction if the weights assigned were optimal.
We calculate this by assuming that if the rating was between the content based
and collaborative filtering predictions than the inaccuracy would be zero
if the weights assigned were optimal. Similarly, the inaccuracy would be
the smaller of the differences between the rating and the content based and
collaborative filtering scores if the rating was either less than or greater
than both the collaborative and the content based predictions.
We also compute the predictions using different techniques of computing the
integrated prediction. The technique used in formula 2 is described in more
detail in section B.1.
Figure 4.5 shows the prediction that is computed by three
different techniques. The curve showing the inaccuracy of the prediction
using formula 1 refers to the inaccuracy in the prediction computed when
the prediction was computed as described in section
4.4. The curve showing the prediction
inaccuracy using formula 2 refers to a the computation of the prediction
using a different technique described in section B.1.
The curve labeled Prediction = Mean refers to the inaccuracy in
the prediction when the prediction returned is the mean rating of the
particular user (this is the mean of all the ratings the user has given till
that time). The curve labeled best is the same curve shown in
figure 4.4. We can see that in general the prediction
computed by using formula 2 was more accurate than the prediction computed
by using formula 1. In some cases both the predictions were the same as the
system was unable to compute either the collaborative or the content based score
and therefore the prediction was the same as the score the system was able
to compute. For example, if the system was unable to compute the collaborative
filtering score, then the prediction returned was the same as the content
based prediction, and therefore, was the same in both cases.
Finally, we make the following observations on the integration of
pure collaborative filtering techniques with content based techniques:
The integration of content based techniques with pure collaborative
filtering allows the system to compute a prediction for all users for
most articles.
The integration of content based predictions with pure collaborative
filtering predictions seems to improve the accuracy of the integrated
prediction specially in the initial stages of a collaborative filtering
system.
Our weighted average technique to integrate the prediction performs
fairly well compared to the best a weighted average technique can perform.
The above results suggest that it is useful to integrate content based
filtering with pure collaborative filtering. This is specially true as pure
collaborative filtering techniques do not perform well in the initial stages
and improve as users rate more items. In real life situations, this gets more
difficult as most users stop using the system when they initially see inaccurate
predictions or when the system cannot compute predictions for the particular
user.
Application of correlation thresholds leads to a corresponding
decrease in the inaccuracy of the computation
From all our experimental results,, we have reached the following
conclusions:
There is a drop in the average inaccuracy of the date set with
the increase in the correlation with users that are considered
for the computation of the prediction. i.e. when the correlation
between users is higher, the prediction computed is generally more
accurate.
We feel this is because of the fact that predictions made based
on the opinions of people who have a low correlation with the user
in question is more prone to error as these users do not have
any established pattern of similarity/dissimilarity of opinions
with the user in question. There is very little justification in
considering the opinions of users with low correlation as their
opinion on a particular item does not indicate how the the user
in question might feel about the same item. Considering the
opinions of such users, on the other hand, could potentially harm
the accuracy of the prediction as their opinions could outweigh the
opinions of users with a high correlation with the user in question.
The drop in inaccuracy is much more rapid in the initial
increase in the correlation between users. When the correlation
between users is above a certain value, the inaccuracy still drops
with the increase in correlation between users, but this happens at
a much slower rate. We believe that this is because of the fact that
when the correlation between users is low, many users with a low
correlation with the user in question could overshadow the opinions
of the few users with a high correlation with the user in question.
A prediction made in such a case, is highly prone to error. When the
correlations between users increases, the margin of error in the
prediction is lower as we are increasingly considering only those
people who have similar/dissimilar to us. At this point, people who
do not hava pattern of similarity/dissimialrity are not considered
at all.
Application of user thresholds leads to a corresponding
decrease in the inaccuracy of the computation
We make the following observations from our experiments on user thresholds
on this data
There is a drop in the average inaccuracy of the data set
with the increase in the number of users that are considered for
the computation of the prediction. We feel this is because of the
fact that predictions made based on the opinion of very few people
can be more prone to error. Such predictions can also
have a larger degree of inaccuracy if the few users it is based
on do not agree with the user in question on that particular
article even if they do agree with the user in question on most
other topics.
The drop in inaccuracy is much more rapid in the initial
increase in the number of users (in our experiments this is
when the number of users is increased from the initial value of
five users to a hundred users). When the number of users is
above a certain number the inaccuracy still drops with the
increase in the number of users, but this happens at a much
slower rate.
We believe this is because of the fact that in the beginning
when the users in the system are very few, there are more
cases of articles where the users who normally agree with the
user in question may not agree with the same user on that particular
topic. An example would be if user A and user B agree on most
cases except on romantic comedies. Predictions for user A for articles
on romantic comedies by taking just the rating of user B into account
would lead to an inaccurate prediction. As the number of users
in the system increases, such cases reduce and so there is a
smaller drop in the decrease in the average inaccuracy of the
system.
Application of history thresholds leads to a corresponding decrease
in the inaccuracy of the computation
We have conducted experiments on the data extracted from the EachMovie
database. The data in the EachMovie database had been collected from
real users using a live system that grew over time both in the number
of users as well as the number of articles in the database.
We make the following observations from our experiments on history thresholds
on this data
There is a drop in the average inaccuracy of the data set
with the increase in the history in common between users that are
considered for the computation of the prediction. i.e. when the number
of articles seen and rated in common by users is larger the
prediction computed is generally more accurate.
We feel this is because of the fact that predictions made based
on the opinion of people who have seen very few articles
in common with the user in question is more prone to error.
There is very little justification in assuming that users would
exhibit the same degree of like-mindedness that they have shown in the
past if the number of articles on which this degree of like-mindedness
is computed is very low.
For example, the fact that user A and user B have seen just two
movies in common and have liked both, does not necessarily imply
that the they will have the same opinion of the third movie they
see in common. If, on the other hand, the number of movies seen and
liked in common by user A and user B was two thousand then we
are almost justified in saying that they have similar opinions on
movies and so will have the same opinion on the next movie they
see in common.
The drop in inaccuracy is much more rapid in the initial
increase in the history in common between users (in our experiments
this is when the history in common is increased from the initial
value of five articles to twenty five articles). When the
number of articles seen and rated in common is
above a certain number the inaccuracy still drops with the
increase in the history in common, but this happens at a much
slower rate.
We believe this is because of the fact that in the beginning
when the number of articles seen and rated in common between
any two users is low, the correlation computed between the
users is based on very few articles and therefore is unstable.
A new article that the two users see in common could change
the correlation between the article by a large margin
leading to a corresponding error in the prediction computed.
As the history in common between two users increases, this
correlation between the users stabilizes and reflects the
actual similarity in the users' profiles more accurately.
Thus a prediction based on such stabilized correlations
are accurate at the onset and so any further increase in the
history does not increase the accuracy of the prediction much.
This is the reason that the inaccuracy of the prediction drops
at a much slower rate with any further increase in the history
in common between users.
Applying of history thresholds lead to predictions that are
more consistently accurate
We have seen that the standard deviation of the error in the prediction
decreases with increasing history thresholds. As 60 percent of the
total predictions lie within one standard deviation of the error, a
decrease in the standard deviation means that 60 percent of the inaccuracies
in the predictions lie within a small range of the average inaccuracy in
the prediction.
This implies that predictions computed are more consistent. As earlier
results show that the inaccuracy decreases with the history thresholds,
this implies that the algorithm gets more consistently accurate
with increasing history thresholds.
Applying of normalization to the predictions is not very useful
for real life data sets.
Though we have conducted experiments on varying sizes and shapes of
data sets we haven't come across a single case where the prediction
made by the system is outside the valid range of ratings allowed.
We therefore conclude, that such situations, though possible
theoretically rarely occur. The implementation of normalization
techniques thus seems like a wasteful computation. We therefore
have reached the conclusion that the implementation of normalization
techniques will not yield much benefit.
The amount of information available to individuals is overwhelming. The Web,
along with Usenet News, email, newspapers, books etc. contribute to an
intimidatingly large information space. There is a clear demand for
automated methods that filter as well as locate information with respect
to users' individual preferences.
Collaborative filtering is a personalized technique to filter information.
Collaborative filtering predicts the ``likability'' of an item based on the
opinions of like-minded users in the system using their statistical correlations
as the weights in a weighted average. These techniques consider the
opinions of all users and therefore can be prone to inaccuracies in
the prediction if the opinions of the few like-minded users get overshadowed by
the opinions of many users with a low correlation. Users with low correlation
do not have a pattern of similarity/dissimilarity of opinions with the user. Their
opinions should ideally not be considered at all. Collaborative filtering also becomes
inaccurate when the correlation between users is based on very few articles seen
in common. Correlations based on a low number of articles in common are unstable
and may not correctly reflect the degree of similarity between two users. We reduce
the collaborative filtering inaccuracy by implementing thresholds.
The basis algorithm [RIS94] computes the prediction by considering the
ratings of all users that have a correlation with the user in question.
We implement correlation thresholds such that we compute the prediction
considering the ratings of only those users who have a correlation higher
than the threshold.
We have shown that the application of correlation thresholds increases the
accuracy of the prediction. There is, however, no correlation threshold that
works best for all the users in the data set. Predictions are most accurate
when correlation thresholds are specific to a user. This correlation threshold
value depends on the number of users who have a correlation above this threshold
value with the user in question.
A side benefit of this improvement is that correlation thresholds provide a
reduction in the computation cost involved in the prediction as the number of
users considered is smaller.
The basis algorithm [RIS94] computes the prediction by
considering the ratings of all users irrespective of the
number of items seen and rated in common between the users. A
problem with this technique is that users may not have seen
enough messages in common to have the correlation between them
accurately reflect their like-mindedness. For example, a history
of only two messages in common and a correlation
of 1.0 is probably not sufficient basis to say that the two users are
likely to agree on the third message.
We implement history thresholds such that we compute the prediction
considering the ratings of only those users who have the number of items
rated in common between them higher than the threshold.
Our experiments show that implementing history thresholds improves accuracy
of the prediction. Although implementing a uniform
history threshold increases the accuracy of the predictions on average,
the best value of the history threshold varies from user to user.
Predictions computed for a user are most accurate when history thresholds
are specific to a user. This threshold depends on the number of users who
are considered for the prediction. The best threshold, therefore, depends
on the number of users who have a history above the threshold with the user
in question.
We have also shown that the application of history thresholds also leads to
predictions that are also more consistently accurate. The standard
deviation of error in the predictions decreases rapidly with increasing history
thresholds making the error in the predictions more consistent. This observation
can be used to get an indication of the
strength of the prediction and can be returned to users to give them an indication
of the confidence they can place in any particular prediction.
Collaborative filtering provides inaccurate predictions to users that do not have
many like-minded users. Also, collaborative filtering does not allow a user to
specify that a particular content be given a higher prediction. Finally, with
collaborative filtering alone, users who are the first to rate an item cannot
get predictions for it. We integrate content based techniques with collaborative
filtering to alleviate the effect of the above problems.
We devise an algorithm that implements keyword matching to perform content based
filtering for news articles. Our algorithm uses the keywords specified in the user's
profile and the articles keywords to compute a content based score. Our algorithm
also uses a set of implicit keywords (extracted from articles liked by the user
in the past) and the news categories (for example, world news, sports etc. ) that
the user has selected to compute different content based scores. We have devised a
technique to integrate these three scores (explicit keywords, implicit keywords and
the category) to compute an overall content based prediction for the user.
We use a weighted average that is adaptable to the relative accuracy of each score
and user specific. The weights assigned to the collaborative and content
based predictions are not only dynamically modified to reflect the user's choice but
are also user specific. This is important as the collaborative filtering prediction
might be more accurate for some users while the content based filtering score
might be more accurate for others, depending upon the correlation and history in
common with other users as well as how well the user has set up her profile.
Our experiments show that the collaborative filtering score is less accurate
in the startup phase of the collaborative filtering system. In extreme cases,
the system is unable to compute a collaborative filtering score for a user. This
can happen if the user is the first person to rate the article or if the system
is unable to compute a correlation for the user
with any other user (a user has to have rated at least two articles in common with
another user for the system to be able to compute a correlation between them).
We also see that in this startup phase the integration of the collaborative
filtering score with a content based score leads to predictions that are more
accurate. At the very least, it allows the system to compute some prediction based
on the content based score if the system is unable to compute a pure collaborative
filtering score. We have also shown that the integration of content based filtering
techniques allows the system to compute a score for new users who have not rated
a single article. The only case when the system is unable to compute a prediction
is when the prediction is being computed for a new user who has not specified
anything in the profile and is reading the first article.
We implement each of the improvements individually and show that they
return a benefit over the basis algorithm. We have seen that correlation
thresholds do not improve the acuracy of predictions unless the
number of users is above a certain minimum. This, for example, suggests
that the implementation of correlation thresholds in conjuncture with
users thresholds would be more beneficial. Though most of the individual
improvements lead to an increase in the accuracy, we feel that
implementing all the improvements would lead to more accurate predictions.
For our off-line experiments we have assumed that all articles belong to
the same information space. That is, the correlation between users that
we compute and consider for the prediction is based on all the
articles that both the users have rated. Let us assume that the users
have rated articles on different topics and have different degrees of
correlation for each topic/category of the information space.
A pair of users can have a high correlation on certain topics and a really
low one on others. In this case, the system does not efficiently use the
high correlation even if it is computing a prediction for an article in
the category where the users have a high correlation.
For example, consider the case where two users A and B always agree
on the movies they see (have a high correlation for movies) but do not
agree on most other topics (they have a low overall correlation).
In this case, though user A has a low correlation with B in general, user A
would still like the system to give a higher weight to the rating of
user B for all articles on movies. We do not implement non-linear
correlations in our off-line experiments.
We believe that computing separate correlations for different information
categories for a pair of users will be more effective than computing
one overall correlation between users.
Our experiments use the ratings given by a pair of users for all the
articles/movies seen in common to compute a correlation between them.
This includes those articles/movies that are universally liked (liked
by most users in the data set) or disliked. It can be argued that
such articles/movies are not really as useful in capturing the similarity
between users as less universally liked/disliked ones. We can extract
the actual similarity between two users' opinions if we compute the
correlation based on just those articles/movies that are not universally
liked or disliked. Such a technique might improve the accuracy with which
the correlation captures the degree of similarity between people and
thus improve the prediction.
In our content based filtering algorithm we perform a keyword matching of
the user's profile and the article's keywords. We generate the article's
keywords from it's text. Words falling between a lower and upper cutoff
(refer section 4.2.2)
are considered to be the keywords of the article.
In our work, these cut-offs have been set to one-fourth and three-fourths
of the rank order of the words. We feel that a study on the determination of
these cut-offs and thus choosing the best cut-offs might improve
the performance of the content based filtering algorithm thus improving the
performance of the integrated algorithm.
For keyword matching in the content based algorithm we use the stems of
words (the part of the word that remains after the word is stripped of
it's suffix). Most
words reduce to the same stem when the largest suffix is removed from them.
For example, both ``facts'' and ``factual'' reduce to the stem ``fact''
when the largest suffixes in the respective words, s and
ual, are removed). Some words, on the other hand reduce to
different stems even when they are essentially the same. For example,
``absorption'' and ``absorbing'' reduce to the stems ``absorp'' and
``absorb'' and will be treated as occurrences of different words.
One way to reduce this problem would be to construct equivalent stem endings
and then use these to identify similar words. In this case, ``absorb''
and ``absorp'' are equivalent stem endings. Implementing these techniques
should lead to somewhat more accurate content based scores and therefore better
predictions.
The accuracy of the keyword matching technique also depends on how accurately the
keywords extracted from an item reflect its content. Removal of common words (such
as articles) by pre-processing the content with a 'stop-list' before extracting
keywords for the article might improve the accuracy of the keyword matching
technique to compute a content based prediction.
We used the keyword matching technique on the user's profile and the
article keywords to compute the content based score. Once disadvantage of
the keyword matching technique is that it depends on the exact word
(the word ``stem'' in our system) and does not exploit the semantic
content of the keywords. This can lead to inaccuracies as people
use different words to to describe the same concept. Latent semantic
indexing (LSI) overcomes this problem of variability in human word
choice by automatically organizing textual information into a semantic
structure into a semantic structure more appropriate for information
retrieval. Using LSI to compute the content based
score might lead to more accurate content based scores as LSI does
not depend on exact word matching and will therefore perform better
content analysis.
The complete content based algorithm in section 4.3 computes
three different scores to compute the content based score. These scores,
Me, Mi and Mc are based on the keyword matching
between the user's profile and the explicit and implicit set of keywords for
the article. These scores are then integrated using a weighted average
to compute the complete content based score. The weights given to each
of these scores by us are equal and are arbitrarily assigned.
Future work in the correct assignment of weights to these scores will improve
the content based score and thus the integrated prediction.
We integrate the content based and the collaborative filtering predictions using a
weighted average. Both the predictions are assigned equal weights in the beginning.
These weights are dynamically modified depending upon which prediction is closer to
the actual rating submitted by the user. A future work in this direction is to
investigate hill climbing techniques as a means of adjusting the collaborative and
content-based weights.
One limitation with the Pearson's correlation coefficient we use
is that it depicts a linear relationship. If a pair of users
have a strong correlation but it is nonlinear then this may not be
reflected as a strong correlation and used as such by the system.
For example, consider two users A and B such that they have a low correlation
when B likes an item but have a high correlation whenever B dislikes the item.
This means that they dislike similar items but may not like similar items.
The system should ideally be able to use this information so that B is treated
as a ``similar'' user for A whenever B gives a low rating for an article.
When calculating a prediction for an article for
user A such that this article has been given a low rating by user B,
the rating given by user B should be given a higher weight when the system
computes the prediction.
Our collaborative filtering system cannot compute a collaborative
filtering score for a new article that no users in the system have
read. The new article has
not been rated by any users and therefore the system does not have
any ratings for the article making it impossible to compute
the prediction for this article for any user. At least one user has to
first rate an article before the system can calculate the collaborative filtering
score for any other user for that article. The system handles such
situations by just returning a content based score based on the users
profile and the article's keywords. Such situations can be dealt with
if the system also maintains correlations between articles. For example,
if two articles get a similar rating by the same user then this means that
the two articles are similar. Articles can conceivably be similar in
content if the content based scores returned for them are similar.
Thus when a new article enters the system, users can be given a prediction
for the article by checking which articles are similar to the new article
and using the ratings given by the user for all such articles to calculate
the prediction.
The goal of collaborative filtering system is to help people focus on
reading documents that would be of interest to them. This requires either
filtering documents that are not relevant or computing a score related to each
document that represents how much the user would like the document. Our
system takes the latter approach.
We have seen on our experiments on the EachMovie data that the accuracy of
such a score for a document depends a lot on the number of people who have
seen articles in common with the user for whom the score is computed. It
also depends on the number of articles seen in common between the user in
question and any other user whose rating is considered for the
computation of the score. Both the above mentioned factors imply that
collaborative systems work well when lots of users have rated lots of articles
in common. The accuracy of the prediction (or score)
may depend on the sparsity of the data set (we define sparsity as the total
number of ratings in the system vs the product of the total number users
and articles).
We conducted experiments to study the effects of the sparsity of the EachMovie data set over time and the corresponding accuracy of the data set.
We ran our experiments to observe the change in sparsity of the
data set over time. Any data set grows over time as the number of
articles coming into the system increases. Data sets also grow as
more users join the system. An increase in the size of the data set
does not necessarily mean a change in the sparsity of the entire
system as users joining the systems may read very few articles either
increasing the sparsity or not affecting it much.
We therefore ran experiments on the EachMovie Dataset to observe
the change in sparsity over time.
We also ran these experiments to see if the average inaccuracy of the
of the predictions of the data set correlate with the
sparsity of the system. As we mentioned earlier, the number of users
who have a correlation in common with the user and the number of
articles read in common affect the accuracy of the prediction. This
implies then that it is not just the sparsity of the data set but the
pattern of distribution of ratings that affect the prediction.
We conduct experiments on the accuracy and sparsity of the data set
over time to evaluate our hypothesis.
Figure:This graph shows a possible distribution of ratings in a data set where some users have given ratings for all articles in the data set. Each point (x,y) represents the fact that a rating has been submitted by the user x for the article y.
Figure:This graph shows a possible distribution of ratings in a data set where some articles have been given ratings by all users in the data set. Each point (x,y) represents the fact that a rating has been submitted by the user x for the article y.
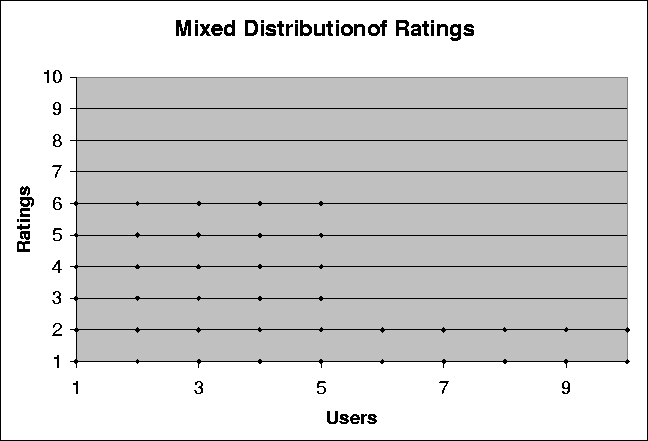
Figure:This graph shows a possible distribution of ratings in a data set where some articles have been given ratings by all users in the data set and some users have given ratings for all the articles in the data set. Each point (x,y) represents the fact that a rating has been submitted by the user x for the article y.
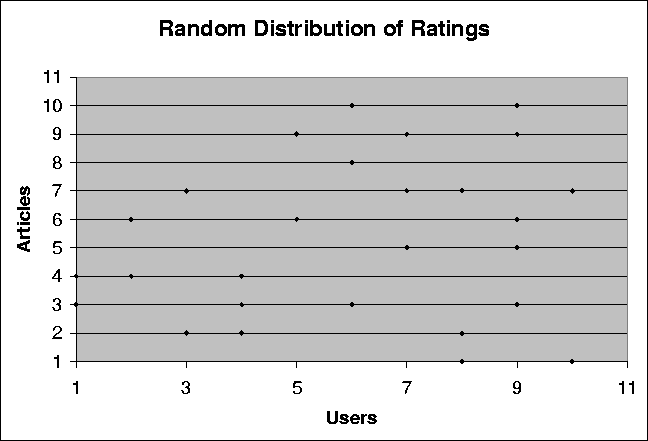
Figure: This graph shows a possible distribution of ratings in a data set where all the users have given ratings for some articles (not necessarily the same articles) in the data set. Each point (x,y) represents the fact that a rating has been submitted by the user x for the article y.
The figures A.1, A.2, A.3 and
A.4 have the same sparsity (50 percent sparse). Each of
the above data sets though have different distributions of the ratings
stored in the data sets. Figure A.1 shows a data set
where all the users have rated th first few articles. In this case,
every user has a correlation with every other user. All the users also
have rated 50 percent of the total articles in common. No user
has rated the other 50 percent of the articles. In this case, it would
be impossible to give a pure collaborative filtering prediction for any
of the latter 50 percent of the articles for any user.
Figure A.2 shows a data set where 50 percent of the users
have rated all the articles and the other 50 percent of the users have
rated no articles. In this case, since the latter 50 percent of the users
have rated no articles, no prediction can be given for any article for
any of the latter 50 percent of the articles. The latter 50 percent of the
users have no correlation with any other user as they have rated no
articles. No prediction can be thus be calculated for these users.
Figure A.4 shows a data set where the history in common
between users is varying. This means that for some users the predictions
will be more accurate than others. Also some users may not have any
articles in common with another user and so will have no correlation
value with this other user.
We ran experiments to observe the effect of the sparsity of the data set
on the average accuracy of the data set. These experiments were carried out
to see if the accuracy of the data set increased with a decrease in the
sparsity (higher ratio of actual number of ratings to total possible
ratings in the data set) or was affected by the factors stated above.
Figures A.6 and A.5 show the
sparsity and inaccuracy of the data set with time.
We can see from figures A.6 and A.5
that both these values (sparsity and
inaccuracy) of the data set are not a function of time. They neither
increase or decrease steadily with time. Also the inaccuracy of the
data set does not change inversely with the sparsity.
We can thus safely say that the inaccuracy of the data set is not a function
of the absolute sparsity of the data set. The data set does not get
more accurate as more ratings are entered into the data set. Rather,
the inaccuracy depends on the way these ratings are distributed. This
means that a collaborative filtering system may not get more accurate
with the addition of more users or articles.
This supports our hypothesis that the accuracy of the
prediction is a function of the history in common between users and the number
of users any particular user has a correlation with. This, in turn, depends
upon the way the ratings are ``distributed'' in the data set.
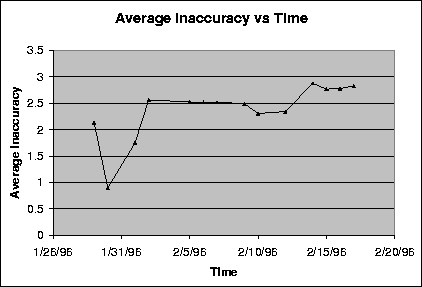
Figure:This graph represents the average inaccuracy of the data set over time. The average inaccuracy of the data set is calculated by taking the average of the inaccuracies in the predictions for every user for every article.
Figure:This graph represents the sparsity of the data set over time. The sparsity of the data set is calculated as the ratio of the total number of ratings in the data set and the total number of possible ratings in the data set.
For data sets where the number of users is large and the number of
articles read in common is above a certain threshold, application of thresholds
yields little benefit in the accuracy of the prediction. This is typically true
for data sets which are ``vertical'' in shape and have very few (or none) of the
users having a high correlation with another user. That is, for data sets where
the ratio of users to articles and the number of articles read in common is big.
This is so as such data sets typically have a low correlation among users as the
users have seen a lot of articles in common and so the chance that any two users
agree on almost all the articles (which would lead to a high correlation ) is low.
The application of thresholds though does not adversely affect
the prediction (as long as the number of such users having a
correlation above the threshold is reasonable) but leads to a benefit
in the computation time.
We have found that the implementation of correlation thresholds yields to
an increase in the accuracy for data sets that are horizontal in nature. That is,
for data sets where the ratio of user to articles read in common by users is low.
This is because users have a low to medium correlation with other users. Applying
correlation threshold for such data sets excludes the users having a low correlation
with the user in question. This leads to both a benefit in the accuracy of the
prediction and the computation time. We also note that the application of correlation
thresholds without the application of user thresholds can sometimes have adverse
effects as the inaccuracy increases if the number of users above the threshold drops
below a certain value.
At time t=0
final prediction = 0.5 * collaborative filtering score + 0.5 * content based filtering Score
Each time a user returns a rating for an article:
Check the collaborative filtering score, content based score and
the rating returned by the user for the article.
Calculate tempWeight1 = old Weight of content based score + (content based score-rating)/(collaborative filtering score-rating)(content based score-rating).
Calculate tempWeight2 = old Weight of content based score + (collaborative filtering score-rating)/(collaborative filtering score-rating)(content based score-rating).
new weight for content based score =
Average of the tempWeight1 and all the distinct weights in the past.
new weight for collaborative filtering score =
Average of the tempWeight2 and all the distinct weights in the past.
N.J. Belkin and B.W. Croft.
Information Filtering and Information Retrieval: Two Sides of the
Same Coin?
Communications of the ACM, 35(12):29-38, 1992.
Chumki Basu, Haym Hirsh, and William Cohen.
Recommendation as Classification: Using Social and Content-Based
Information in Recommendation.
American Association for Artificial Intelligence, pages
714-720, 1998.
Daniel Billsus and Michael Pazzani.
Learning Collaborative Information Filters.
Machine Learning: Proceedings of the Fifteenth International
Conference, 1998.
W.B. Croft and Das.
Experiments with query acquisition and use in document retrieval
system.
In ACM SIGIR Conference on Research and Development in
Information Retrieval, pages 349-368. ACM, 1990.
S. Deerwester, S.T. Dumais, G.W. Furnas, T.K. Landauer, and R. Harshman.
Indexing by Latent Semantic Analysis.
Journal of the American Society for Information Science, pages
391-407, 1990.
P.W. Foltz and S.T. Dumais.
Personalized Information Delivery: An Analysis of Information
Filtering Methods.
Communications of the ACM, 35(12):51-60, 1992.
G.W. Furnas, S. Deerwester, S.T. Dumais, T.K. Landauer, R.A. Harshman, L.A.
Streeter, and K.E. Lochbaum.
Information retrieval using a singular value decomposition model of
latent semantic structure.
In Proceedings of the 11th Conference on Research and
Development in IR, pages 465-480. ACM/SIGIR, June 1989.
W.C. Hill, J.D. Hollan, D. Wroblewski, and T. McCandless.
Edit Wear and Read Wear.
pages 3-9. CHI '92 Conference on Human Factors in Computing Systems,
1992.
W.C. Hill, J.D. Hollan, D. Wroblewski, and T. McCandless.
Using Collaborative Filtering to Weave an Information Tapestry.
Communications of the ACM, 35(12):61-70, 1992.
Joseph A. Konstan, Bradley N. Miller, David Maltz, Jonathan L. Herlocker,
Lee R. Gordon, and John Riedl.
GroupLens: Applying Collaborative Filtering to Usenet News.
Communications of the ACM, 40(3):77-87, March 1997.
B.J. Lovins.
Error Evaluation for stemming algorithms as clustering algorithms.
Journal of the American Society of Information Science,
29:390-404, 1973.
K.H. Packer and D. Soergel.
The importance of SDI for current awareness in fields with scatter
of information.
Journal of American Society of Information Science,
30:125-135, 1979.
Paul Resnick, Neophytos Iacovou, Mitesh Suchak, Peter Bergstrom, and John
Riedl.
An Open Architecture for Collaborative Filtering of Netnews.
pages 175-186. ACM Conference on Computer Supported Co-operative
Work, 1994.
Badrul M. Sarwar, Joseph A. Konstan, Al Borchers, Jon Herlocker, Brad Miller,
and John Riedl.
Using Filtering Agents to Improve Prediction Quality in the
GroupLens Research Collaborative Filtering System.
Computer Supported Cooperative Works 1998 Conference, 1999.
Seattle.
Loren Terveen, Will Hill, Brian Amento, David McDonald, and Josh Creter.
Phoaks: A system fro Sharing Recommendations.
Communications of the ACM, 40(3), 1997.
Although recently published
literature on research in filtering techniques have used the term
collaborative filtering interchangeably with the terms social
filtering and recommender systems, we shall henceforth use the
term collaborative filtering to refer to any three of the above
have shown that the Web is filled with transient information.
In 1996, there were an estimated 50 million pages on the Web and each
page was online for only an average of 75 days. Other recent
surveys have estimated the number of Web users
in the U.S. as of May 1998 at 57,037,000 and the number of Web pages as
of April 1998 at approximately 320 million [Tre98b]!
Furthermore, the number of pages is doubling every year. Using
the average Web page size of 30 kilobytes (including graphics)
brings the current size of the Web to 1.5 terabytes (or
million megabytes).
