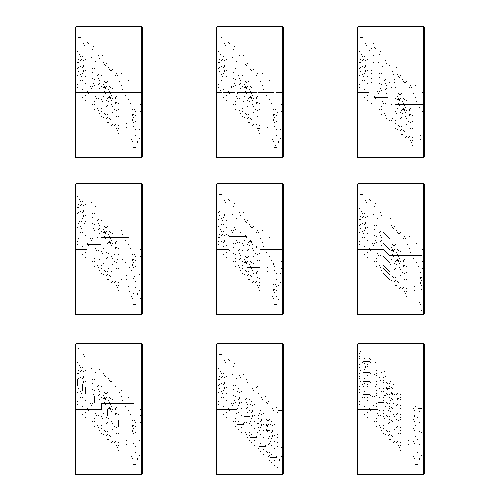SEQUENCE ANALYSIS USING CORRELATION IMAGES

Matthew Ward, WPI CS Department

A sequence is a string of entities from a finite alphabet with some ordering relationship, e.g. text, shapes, music, speech, pictures. Relationships between sequences include equality, containment, cyclicly equal, or partial overlap, along with differences caused by substitutions, insertions, deletions, swaps, compressions, and expansions. Relationships between entities in a sequence can be binary (equal/not equal) or multilevel.

A Correlation Image (CI) is a visual representation of all possible alignments between 2 sequences. For 1-D sequences, each row corresponds to a different alignment of the sequences, and the intensity of each pixel is proportional to the goodness of match of the aligned entities.

The following is a list of perceptible structures within the CI and the generalized sequence relationship which created them.

Horizontal Lines: consecutive matches
Broken Horizontal Lines: substitutions
Shifted Horizontal Lines: insertions, deletions, transpositions
Horizontal Lines Joined by Diagonals or Verticals: compressions, expansions
Vertical Lines (continuous or broken): distribution of entity in first sequence over the second
Diagonal Lines: distribution of entity in second sequence over the first
Textures: distribution of groups of entities in one over the other

This image shows examples of each of these phenomena. .

XSauci (X-window Sequence Analysis using Correlation Images) is a system developed at WPI by David Nedde and Matt Ward (with later enhancements by Maureen Higgins) for exploring the application of CIs to genetic sequence analysis. The following is a partial list of the features of XSauci:

Dynamic filtering of short match segments
Context-sensitive gap filling
Feature-preserving compression for large sequences
Database browsing capabilities
Single sequence reading frame analysis
Visualization of codon density and distribution

Biologically significant relationships can be localized by searching for the features listed below.

Insertions/Deletions: Horizontal lines shifted vertically
Direct Repeats: Horizontal lines stacked vertically
Indirect Repeats: Horizontal lines (must invert one sequence)
Hairpins: Horizontal lines (must invert and complement sequence and run against itself)
Homologies between 2 sequences: Horizontal lines, perhaps broken and shifted

Another project involving CIs was in text analysis, resulting in a system called vdiff, by David Gosselin. Blocks of text can be compared by character or word, with both exact and partial matching capabilities. Small segments of the CI could be displayed as aligned text instead of pixels.

A recent thesis by John Rasku explored the use of CIs in comparing shapes. By representing a shape as a sequence of elements (we tried the coordinates themselves, first and second derivatives, and distance to centroid) with a distance metric, we could classify the way different shape changes manifested themselves within the CI and which representation(s) were best for various shape differences. We did a simple experiment with 3-D shapes as well (represented as a series of 2-D slices), though it was clear that better 3-D representations were needed.

matt@owl.WPI.EDU