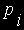 at parameter u is:
at parameter u is:
by Suzanne Martin
Free-form deformation (FFD) is an important tool in computer-assisted geometric design and animation. Barr [BARR84] developed a method which altered the transformation while it was being applied to the object. A more general technique was later developed by Sederberg and Parry [SEDE86] which deformed objects by deforming the space in which the object is embedded. Another method was developed by Coquillart [COQU90] which used an initial lattice and B-spline control points to approximate the shape of the intended deformation. Below is a brief discussion of the above methods followed by an explanation of a technique developed by Chang and Rockwood [CHAN94].
The de Casteljau Algorithm for evaluating a Bézier curve of degree n with
control points 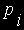 at parameter u is:
at parameter u is:
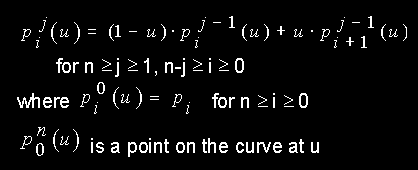 .
.
The Chang and Rockwood method takes the above repeated univarite linear interpolation and generalizes it to a trivariate method. A local coordinate system is defined for each segment of the Bézier control polygon. It is defined at one endpoint by 2 user-specified axes, called "handles". The objects are then mapped along an embedded Bézier curve by applying iterative affine transformations using the handles and control polygon segments. The following four figures are an example of this:
Figure 1: Quadratic Bézier curve, control polygon and
two user-specified axes
Figure 2: Cube to be deformed
Figure 3: First-level execution of the generalized
de Casteljau algorithm the cube is mapped
affinely to each segment of the control
polygon
Figure 4: Second-level execution of the generalized de Casteljau
algorithm the original cube is warped along the Bézier curve
Let vectors r, s, t span affine space. Function Ø[p,q]: R^3 -> R^3 is then defined as an affine transformation from parameter space into homogeneous form
|u| |qx - px sx tx px| |u| |x|
Ø[p,q] |v| = |qy - py sy ty py| |v| = |y|
|w| |qz - pz sz tz pz| |w| |z|
|l| | 0 0 0 1 | |1| |1|
where r_vector = (qx - px, qy - py, qz - pz), s_vector = (sx, sy, sz) and
t_vector = (tx, ty, tz).
The generalized de Casteljau algorithm is:
for 0 <= i <= n,
= Ø [
,
] (u) for 1 <= j <= n, 0 <= i <= n-j, where n is the degree and
is the deformed point on the object at u_vector = (u, v, w). Iterative affine transformations are applied resulting in the Bézier curve being part of the deformation space. The result of an iterative affine transformation: Level 1 of the generalized de Casteljau algorithm: If the s_vector in the transformation matrix equals a 0 vector, then the solid will be mapped into just a surface patch. The depth information is lost. If the t_vector equals a 0 vector then the degeneration is similar to the s_vector as described above, but degeneration occurs on a different axis. If both the s_vector and the t_vector equal 0 vectors, then the deformation process becomes the classic de Casteljau algorithm. Since parameters v and w are no longer effective, the solid is mapped to the curve. Levels 2 and higher: If the s_vector and the t_vector are all zero, the function blends the result of the first-level execution linearly. If sx, sy or sz is nonzero, the deformed object is sheared by an amount proportional to the v value along the direction of (sx,0,0) or (0,sy,0) or (0,0,sz). The same applies to the t_vector, but shearing proportional to w instead of v. The effects of shearing are hierarchical. For example: there are 3 levels of affine transformations in the cubic case. A nonzero s_vector or t_vector in the second-level transformation matrix, shears only the portion of the object related to the appropriate control polygon segments. A nonzero s_vector or t_vector in the third-level affects the whole object.
Below is a comparison of the computation times between these methods.
-------------------------------------------------------------------------------------
| | |
Deformation\ Degree | Linear | Quadratic | Cubic
| | |
=====================================================================================
| | |
Bézier lattice method | 42 multiplications | 90 multiplications | 144 multiplications
| | |
Sederberg and Parry | | |
approach | 21 additions | 45 additions | 72 additions
| | |
----------------------|--------------------|--------------------|--------------------
| | |
Generalized de | | |
Casteljau method | 9 multiplications | 27 multiplications | 54 multiplications
| | |
Chang and Rockwood | 9 additions | 27 additions | 54 additions
| | |
----------------------|--------------------|--------------------|--------------------
[BARR84] Barr, A. H., Global and Local Deformations of Solid Primitives, Proceedings of SIGGRAPH ‘84, Computer Graphics 18, 3 (July 1984), 21-30.
[CHAN94] Chang, Y.and Rockwood, A. P., A Generalized de Casteljau Approach to 3D Free-form Deformation, Proceedings of SIGGRAPH ‘94, Computer Graphics (July 1994), 257-260.
[COQU90] Coquillart, S., Extended Free-Form Deformation: A sculpturing Tool for 3D Geometric Modeling, Proceedings of SIGGRAPH ‘90, Computer Graphics 24, 4 (August 1990), 187-196.
[SEDE86] Sederberg, T. W. and Parry, S. R., Free-Form Deformation of Solid Geometric Models, Proceedings of SIGGRAPH ‘86, Computer Graphics 20, 4 (August 1986), 151-159.
matt@owl.WPI.EDU