CS 2223 Apr 12 2021

Lecture Path: 12
Back Next

Musical Selection: Peter Cetera: Glory of Love (1986)

Visual Selection: Sistine Chapel Ceiling, Michelangelo (1508-1512)

Live Selection:Spirit of Radio, Rush (2012)

Daily Question: DAY12 (Problem Set DAY12)

1 Heap Processing

1.1 Interview Challenge

1.2 HW2

Opening discussion of HW2 here. Due Apr 15 2021 at 10AM.

• In your MyDeck(max_rank) constructor, you need to remove restriction on the max rank, to allow it to for up to 20...

• In your Q3, the documentation showed sample output, but in the second table, the values in the second column are wrong.

Note that HW3 is to be assigned on Apr 16 2021 and will be due on Apr 27 2021.

1.3 Discussion of Modulo operator

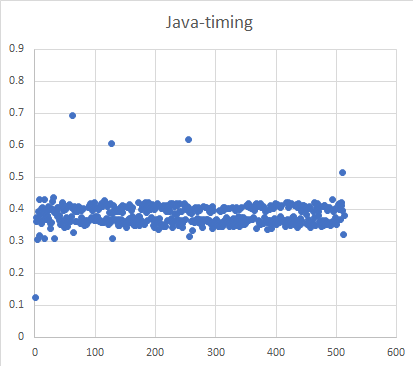
In lecture on Friday I was discussing the implications of using modulo operators as a costly operation. A student pointed out that the compiler should optimize modulor operators, but this is only possible if the constant is part of the code (rather than dynamically in a variable). Still, I thought to investigate. I posted the result in Canvas: find in files | in-class exercise | Day 12 Comparison Modulo. Hopefully the following image will inspire you to check out the numbers in more detail:

1.4 HeapSort

Now that you have seen a Heap structure, we need to understand how to build a heap from scratch, and how it can be used in an interesting sorting algorithm called Heap Sort.

1.5 Building a Heap

On page 318 of the book, you can see the disarmingly simple code for adding an element to a heap. In this case, we assume there is enough room in the array, but you should know how to add the necessary code to dynamically resize the array to add more space as needed.

public void insert (Key v) { pq[++N] = v; swim(N); }

This code first pre-increments N – recall that the 0th element of the array is not being used to make the indices easier to compute. Remember that a heap must maintain its Heap shape property, which means that you don’t add a new item to a level until the previous level is complete, and each level is filled from left to right in order. The pq[++N] = v statement does just that.

Once inserted, this new value might violate the Heap ordering property, so you have to invoke swim(N) to make sure that all ancestors are properly updated to abide by this property.

1.6 In-class exercise

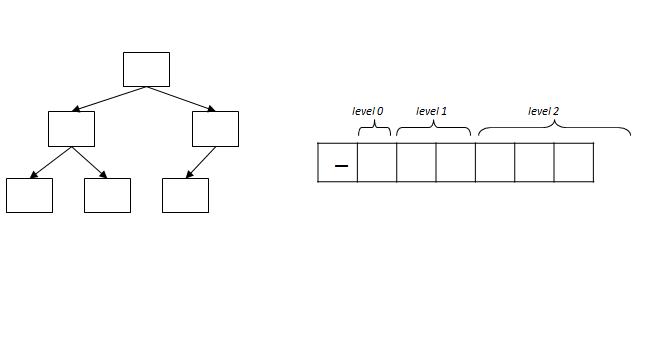
Use this process to build a heap after the following values have been added in the following order:

2, 7, 4, 9, 8, 6

Assuming the array has enough room for the elements, what will be the final array representation in the resulting heap?

1.7 Removing an element from a Heap

Finding the largest element is not an issue becaue the topmost element in the heap a[1] is the largest value. However, once it is removed, what do we replace it with? I guess it could be replaced with the larger of its two children, but we have to be very careful to maintain the Heap Shape Property. Since adding to a heap was simply a matter of adding to the final unused element in the array, perhaps this remove operation could use that value as the replacement and then reduce the size of the heap by one.

public Key delMax() { Key max = pq[1]; exch(1, N−−); // swap final entry to replace root pq[N+1] = null; // to avoid loitering sink(1); // re-establish heap ordered property return max; }

Observe that the delMax operation reduces the number of elements in the array by one, and the Heap Shape Property is maintained by carefully mainpulating the elements. The sink(1) operation resetablishes the Heap Ordered Property and it takes no more than ~ log N operations to achieve this.

Given the final heap we just constructed, demonstrate the resulting array structure after invoking delMax two more times.

1.8 How to use Heap to implement sorting

First observe that the topmost element of the heap is always the largest item. This gives us our first clue. However, if we are to sort "in-place" without any additional storage, what can we do?

Start with an arbitrary array and convert it into a Heap. Note that we now have to ensure that the 0th array location is part of the heap, which is something we didn’t do earlier; however, nothing could be simpler!

The trick is to recognize that all elements are refered to only within the less and exch methods. Therefore, these two methods are changed as follows to reflect 1-based indexing. Thus the 1st element is to be found at index location 0.

static boolean less(Comparable[] a, int i, int j) { return a[i-1].compareTo(a[j-1]) < 0; } static void exch(Object[] a, int i, int j) { Object swap = a[i-1]; a[i-1] = a[j-1]; a[j-1] = swap; }

Note there are still N elements in the array, and they are referred to using 1-based indexing. Again, this was done by Sedgewick to make the computations easier to see and understand.

1.9 Ready to explain HeapSort

There are two steps that we complete. First we need to turn an arbitrary array of values into a Heap.

1.9.1 Convert arbitrary array into heap

Consider the following partial array of values. I use "??" to represent any number. If you look at the picture and squint, the numbers that are present could actually already be in their proper spot for all that you know! Or to put it in other words, each of these elements forms a valid heap of 1 element.

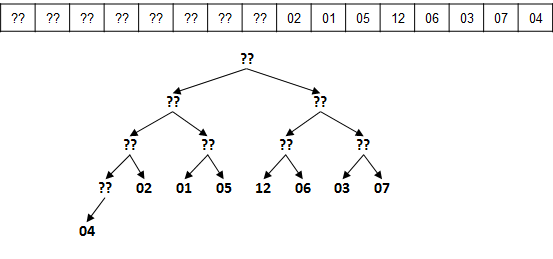
So where is the first element that has a child? If we start counting each element, starting with numbers 1, 2, 3, ... then the position is exactly located at index floor(N/2). See code on (p. 324).

So all we need to do is visit each of the ?? positions in reverse order and call sink on that location to reestablish the Heap ordering property. The code is just a bit more complex because you have to pass in more parameters. First you pass in the array that is being converted into a heap structure; then you pass in N the number of elements, so sink knows when to stop; and you pass in k representing the item location (when counting from 1) to sink:

static void sink(Comparable[] a, int k, int N) { while (2*k <= N) { int j = 2*k; if (j < N && less(a, j, j+1)) j++; if (!less(a, k, j)) break; exch(a, k, j); k = j; } }

This code should be familiar from yesterday. Once all floor(N/2) positions have been processed and the array has been turned into a Heap, the sorting process can begin.

1.9.2 Exchange largest into proper place

With just N-1 iterations, it is possible to sort the heap into an array. The largest element is always in the 1st location, so we first swap this with the final element in the heap and decrement the number of elements in the array. This results in an array of N-1 elements and all you need to do is reestablish the Heap Ordered Property starting with the 1st element. Here is what the full sorting code looks like:

public static void sort(Comparable[] a) { int N = a.length; for (int k = N/2; k >= 1; k−−) { // (1) Create Heap from array sink(a, k, N); show(a); } while (N > 1) { exch(a, 1, N−−); // (2) Modify in place, sink(a, 1, N); // exch. max } }

As you review the code above, you can see that the step "(1) Create heap from array" consists of a for loop that executes N/2 times. Each time through, it calls sink, which we have already seen. As you should recall, the worst case performance for sink is directly proportional to log(N). So at first, this loop appears to take (N/2)*(log N). It seems suprising, and can be validated empirically, that the total number of comparisons needed to build the initial heap will be 2N; the intuition behind this result is that it is simply impossible to continually experience the worst case as you work your way (backwards!) calling swim. Hopefully the example will reveal this when you work it out by hand.

We will work through example in class.

1.10 Tilde Notation

The book covers Tilde notation in pages 180-187. As I’ve said in class, we are moving to a more formal notation to use, and this will become increasingly important for the remaining homeworks.

There are two skills that you need to do:

Code Analysis: Given a block of code, analyze the order of growth (as a function of N) of the running time of the code fragment. Consider the following code. Think of the frequency of execution of the outer loop and the inner loops (see p. 181 for details).

int sum = 0; // Block A for (int n = N; n > 0; n /= 2) { // Block B for (int i = 0; i < n; i++) { // Block C sum++; } }

t1: A executes 1 time
t2: B executes ________ times
t3: C executes ________ times

Grand Total: ____________

The resulting Ordering Of Growth is going to be based on the formulae found on p. 187:

• 1 – constant

• log N – logarithmic

• N – linear

• N log N – linearithmic

• N2 – quadratic

• N3 – cubic

• bN – exponential (in any base b>1)

1.11 Sample Exam Question

The following exam question is just a bit too hard to ask on the exam. But try it out and we will review in the next lecture:

You have an array of N elements in sorted order. You wish to use Binary Array Search to determine the rank for a target value, x. The only problem is, the compareTo(a, b) operator will lie exactly one time during your search. This function returns 0 if the values are the same, a negative number if a < b, and a positive number if a > b.

Complete the following skeleton algorithm (in pseudo code or Java code) and then identify the fewest number of less requests that your algorithm needs to accurately determine the rank of x.

(a) Design your algorithm in Java or pseudo code

int rank (Comparable[] a, Comparable x) { // fill in here... }

(b) Compute the fewest number of less requests needed in terms of N where N is the number of elements in the Comparable[] array.

1.12 Daily Question

The assigned daily question is DAY12 (Problem Set DAY12)

If you have any trouble accessing this question, please let me know immediately on Discord.

1.13 Version : 2021/04/18

(c) 2021, George T. Heineman