CS 2223 Apr 09 2021

Lecture Path: 11
Back Next

Musical Selection: Simple Minds: Don’t You (Forget About Me) (1985)

Visual Selection: School of Athens, Raphael Sanzio (1509-1511)

Live Selection: A little help from my friends, Joe Cocker (1968) Lennon/McCartney (1967)

Daily Question: DAY11 (Problem Set DAY11)

1 Priority Queues

1.1 HW2 updates

For questions 1.1 and 1.2 my instructions were not clear. For these two questions, you should write a class that looks like this:

package USERID.hw2; public class Q1 { public static void main(String[]args) { for (int max_rank = 1; max_rank <= 20; max_rank++) { MyDeck d = new MyDeck(max_rank); // now write code to perform a number of in() shuffles System.out.println(max_rank + "\t" + number); } } }

You only have to come up with a formula when attempting the bonus questions.

1.2 Announcements on office hour updates

If a TA/SA cannot make a regularly scheduled office hour, then an announcement will be posted in Canvas with the adjusted datetime. Please double-check in canvas if you think an office hour is not being covered.

1.3 Sorting Summary

Another general shout!
I do believe that these applauses
are for some new honours
that are heap’d on Caesar.
Julius Caesar
William Shakespeare

We could have spent several weeks on sorting algorithms, but we still have miles to go before we sleep, so let’s quickly summarize. We covered the following:

• Insertion Sort

• Selection Sort

• Merge Sort

• Quick Sort

For each of these, you need to be able to explain the fundamental structure of the algorithm. Some work by dividing problems into subproblems that aim to be half the size of the original problem. Some work by greedily solving a specific subtask that reduces the size of the problem by one.

For each algorithm we worked out specific strategies for counting key operations (such as exchanges and comparisons) and developed formulas to count these operations in the worst case.

We showed how the problem of comparison-based sorting was asymptotically bounded by ~N log N comparisons, which means that no comparison-based sorting algorithm can beat this limit, though different implementations will still be able to differentiate their behavior through programming optimizations and shortcuts.

1.4 Yesterday’s Daily Exercise

How did people fare on evaluating the recursive solution in terms of the maximum number of comparisons?

You should have been able to declare C(n) as the number of comparisons and then defined its behavior as:

C(N) = C(N/2) + C(N/2) + 1

assuming that N=2n as a power of 2.

C(N) = 2*C(N/2) + 1
C(N) = 2*(2*C(N/4) + 1) + 1
C(N) = 2*(2*(2*C(N/8) + 1) + 1) + 1

and this leads to...

C(N) = 8*C(N/8) + 4 + 2 + 1

since N = 2n and we are still at k=3...

C(2n) = 2k*C(N/2k) + (2k-1)

Now we can continue until k = n = log N, which would lead to...

C(2n) = 2n*C(N/2n) + (2n-1)

and since C(1) = 0, we have

C(N) = N - 1

1.5 Homework2

Be sure to replace "USERID" with your CCC credentials. For example, my email address is "heineman@wpi.edu" so my USERID would be "heineman".

1.6 Priority Queue Type

In the presentation on the Queue type, we discussed the nature of a queue as providing a "first in, first out" behavior. One naturally wonders whether it is possible to enqueue elements but then dequeue the element of "highest priority" still in the queue. This is the classic definition of a Priority Queue. To describe this as an API, consider the following operations that would be supported (p. 309):

There are other elements, but these are the starting point.

In our initial description, the Key values being inserted into the PQ are themsevles primitive values. In the regular scenario, the elements are real-world entities which have an associated priority attribute.

One solution is to maintain an array of elements sorted in reverse order by their priority. With each request to insert a key, place it into its proper sorted location in the array.

You could keep all elements in unsorted fashioin and then your delMax operation will take time proportional to the number of elements in the PQ.

No matter how you look at it, some of these operations take linear time, or time proportional to the number of elements in the array. Page 312 summarizes the situation nicely:

The alternate heap structure can perform both operations in log N time. This is a major improvement and worth investigating how it is done.

1.7 Heap Data Structure

We have already seen how the "brackets" for tournaments are a useful metaphor for finding the winner (i.e., the largest value) in a collection. It also provides inspiration for helping locate the second largest item in a more efficient way than searching through the array of size N-1 for the next largest item.

The key is finding ways to store a partial ordering among the elements in a binary decision tree. We have seen this structure already when proving the optimality of comparison-based sorting.

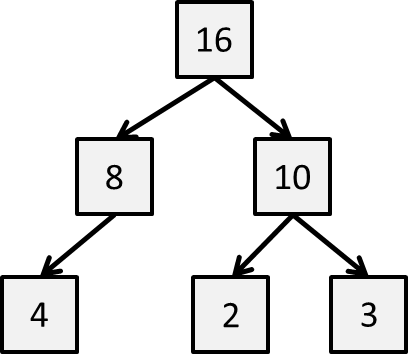
Consider having the following values {2, 3, 4, 8, 10, 16} and you want store them in a decision tree so you can immediately find the largest element.

Figure 1: Binary Decision Tree

1.8 Benefits of Heap

We have already seen how the concepts of "Brackets" revealed an efficient way to determine the top two largest elements from a collection in n + ceiling(log(n)) - 2 which is a great improvement over the naive 2n-3 approach. What we are going to do is show how the partial ordering of elements into a heap will yield interesting performance benefits that can be used for both priority queues (today’s lecture) and sorting (Thursday’s lecture)

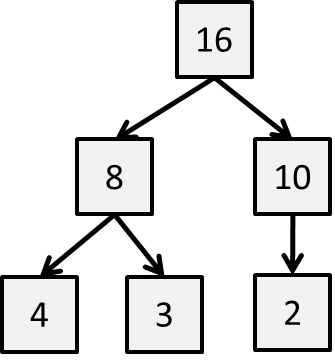
Definition: A binary tree is heap-ordered if the key in each node is larger than or equal to the keys in that node’s two children (if they exist).

But now we add one more property often called the heap shape property.

Definition: A binary tree has heap-shape if each level is filled "in order" from left to right and no value appears on a level until the previous level is full.

While the above example satisfies the heap-ordered property, it violates the heap-shape property because the final level has a gap where a key could have been placed.

Figure 2: Binary Heap

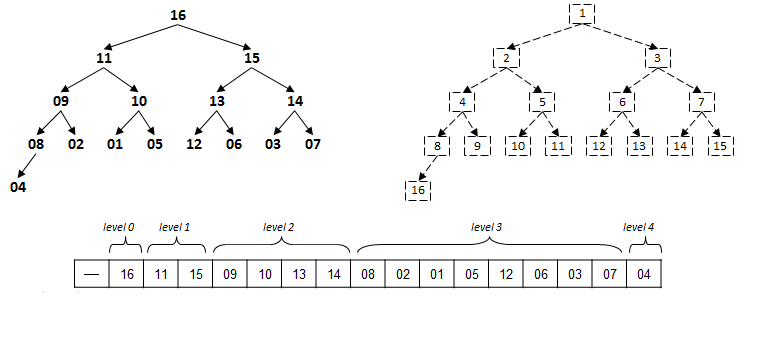
With this model in mind, there is a direct mapping of the values of a heap into an array. This can be visualized as follows:

Figure 3: Larger Heap Example

Each value at index k has potentially two children at indices 2*k and 2*k+1. Alternatively, each value at index k > 1 has its parent node at index floor(k/2).

There are two internal operations needed to maintain the structure of a heap. For now we focus on the mechanisms and you will see their ultimate use in the lecture on Apr 12 2021.

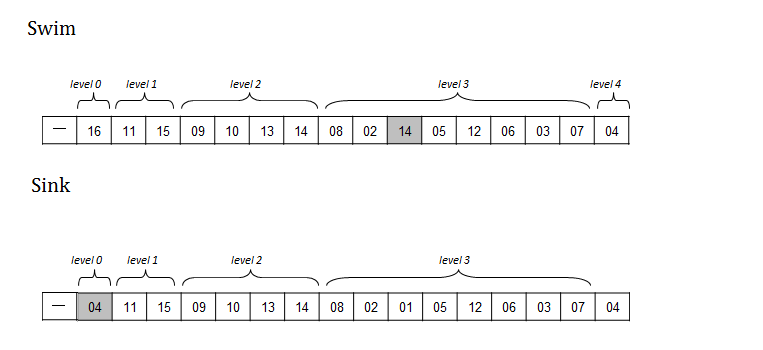
1.9 Swim – reheapify up

What if you have a heap and one of its values becomes larger than its parent. What do you do? No need to reorganize the ENTIRE array, you only need to worry about the ancestors. And since the heap structure is compactly represented, you know that (p. 314) the height of a binary heap is floor (log N). The height of a tree is the maximum depth among its nodes. A heap with just 1 element has a height of 0.

1.10 Sink – reheapify down

What if you have a heap and one of its values becomes smaller than either of its (potentially) two children? No need to reorganize the ENTIRE array, you only have to swap this value with the larger of its two children (if they exist). Note this might further trigger a sink, but no more than log N of them.

Figure 4: In class Example

1.11 Create heap bottom-up or top-down?

The heap is created "bottom up" from position N/2 working back to position 1. An alternate situation would be to create the heap "top down" starting from position 1 and working forward.

N Build Less HS Exch HS BuildLTD Less HS-TD Exch HS-TD 4 4 7 6 4 7 6 8 9 26 17 9 26 21 16 19 77 50 22 81 52 32 50 218 126 52 221 132 64 111 580 332 119 583 348 128 226 1386 785 275 1445 847 256 465 3299 1831 558 3386 1957 512 943 7608 4138 1100 7777 4364 1024 1904 17335 9335 2258 17675 9821 2048 3844 38767 20721 4648 39539 21777 4096 7681 85694 45571 9313 87295 47701 8192 15328 187615 99121 18445 190749 103379 16384 30736 408056 214656 36942 414285 223106 32768 61705 882215 462514 75014 895336 480310 65536 123114 1894400 989784 149153 1920296 1024828 131072 246441 4051705 2111425 298730 4104495 2181889 262144 493122 8627926 4484693 597255 8731865 4624987 524288 986644 18304455 9493221 1195898 18514463 9776455

1.12 Daily Exercise

In an array, a repeater, is a value which appears more than n/2 times in an array of size n.

For this daily exercise, what if you had a heap of size n stored in an array and you were told that there is a repeater value in the heap. Can you guarantee that one of the leaf nodes is a repeater value? Either prove or provide a counter example.

1.13 Interview Challenge

Each Friday I will post a sample interview challenge. During most technical interviews, you will likely be asked to solve a logical problem so the company can see how you think on your feet, and how you defend your answer.

You have three pair of colored dice – one red, one green and one blue – and for each colored pair of dice, one of the die is lighter than the other. You are told that all of the light dice weigh the same. And also you are told that all of the heavy dice weigh the same.

You have an accurate pan balance scale on which you can place any number of dice. The scale can determine whether the weight of the dice on one side is equal to, greater, or less than the weight of the dice on the other side.

Task: You are asked to identify the three lightest dice from this collection of six dice.

Obvious Solution: You could simply conduct three weight experiments.

1. Put one red die on the left pan, and the other red die on the right pan – this will identify the lighter red die

2. Put one green die on the left pan, and the other green die on the right pan – this will identify the lighter green die

3. 3. Put one blue die on the left pan, and the other blue die on the right pan – this will identify the lighter blue die This takes three weighing operations.

Challenge: Can you locate the three lighter dice with just two weight experiments, where you can place any number of dice on either side of the pan.

1.14 Daily Question

The assigned daily question is DAY11 (Problem Set DAY 11)

If you have any trouble accessing this question, please let me know immediately on Discord.

1.15 Version : 2021/04/11

(c) 2021, George T. Heineman