CS 2223 Apr 23 2018

Lecture Path: 23
Back Next

Expected reading:
Daily Exercise:
Classical selection: Tchaikovsky: Violin Concerto in D major (1878)
Musical Selection: Chumbawamba: Tubthumping (1997)

There are many shortcuts to failure, but there are no shortcuts to true success
Orrin Woodward

1 Big O Notation Completion

1.1 Homework 4 and revised Syllabus

Homework 4 is due tonight at 9PM.

I’ve revised the lectures (and readings) for this week; please review the updated syllabus.

1.2 Empirical Evidence

You will routinely execute your programs and then graph its progress to determine how it will perform with larger and larger problem sizes. We now complete the description of the mathematical tools you need to properly classify the performance of your algorithms.

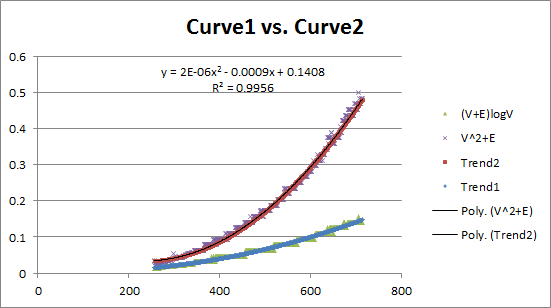
These two curves reflect two different algorithms. Observe that they have different growth behaviors. Is it possible to model these growth curves mathematically?

The performance of the algorithm (on average) appears to be hitting the mark very close to expected. But what happens in the worst case? Indeed, what is the worst case for each of these algorithms?

We want to be able to identify three cases for each algorithm:

best case – the situation in which the algorithm performs the least amount of work.
worst case – the (often pathological) case in which the algorithm must perform the most amount of work.
average case – using statistics and randomness, try to come up with an average problem size to use for expected performance.

For the duration of this lecture, we will be solely interested in worst case performance.

1.3 Loop performance analysis

Regular loops are easy to handle, but we need to take special care with nested loops (including for/while) as well as the latest loops seen with graph structures.

1.3.1 Nested Loops With Integer indices

We have seen several types:

for (int i = 0; i < N; i++) { for (int j = 0; j < N; j++) { statement } }

The above statement will execute N2 times, and this naturally extends to higher orders:

for (int i = 0; i < N; i++) { for (int j = 0; j < N; j++) { for (int k = 0; k < N; k++) { statement } } }

Here the statement executes N3 times. What if the indices are more dynamic?

for (int i = 0; i < N; i++) { for (int j = i+1; j < N; j++) { statement } }

We have seen this format also. When i is 0, statement executes N-1 times, when i is 1, statement executes N-2 times, and so on. It turns out you need to compute the sum of the numbers from 1 to N-1 to determine the proper number of executions of statement. These are the triangular numbers, that is, the Nth triangle number is N*(N+1)/2. In this case we are looking for the N-1th triangle number (starting from N=1) which means the proper computation is N*(N-1)/2 times.

Here is a more complicated situation

for (int i = N; i > 1; i /= 2) { for (int j = 0; j < N; j++) { statement } }

Here the outer i loop executes exactly floor(log(N)) times. What about the inner loop? It continues to execute N times, thus the total number of times statement executes is: N*floor(log(N))

1.3.2 Graph Looping Analysis

Now that we have seen the graph structure, there are more complicated patterns of behavior.

for (int u = 0; u < g.V(); u++) { for (int v = 0; v < g.V(); v++) { statement } }

The inner statement executes V2 times. This is true regardless of whether g is a directed or undirected graph.

However, it is more common to see something like this for an undirected graph.

for (int u = 0; u < g.V(); u++) { for (int v : g.adj(u)) { statement } }

How to interpret in this case? Well, you know that the outer u for loops is going to visit each vertex exactly once. Then the inner v loop visits each neighbor of u.

Adjacency List – If you can recover the neighboring vertices of u in time directly proportional to the degree of u, then statement will execute exactly 2*E times, since each edge is visited twice.
Adjacency Matrix – If you must visit all vertices in the graph to determine the adjacent neighbors, then the time will be directly proportional to V, and so the inner statement will execute V2 times, regardless of how many edges exist in the graph. We will see adjacency matrix implementation in two more lectures.

What about recursive executions, such as dfs? What is the perform of dfs(g, 0)? In this case, Graph is undirected. Note that whenever I refer to a directed graph, I will always call it a Digraph.

void dfs(Graph G, int v) { marked[v] = true; for (int w : G.adj(v)) { if (!marked[w]) { edgeTo[w] = v; dfs(G, w); } } }

First observe that the recursive call only happens because there is an unmarked vertex; after each recursive call the vertex is marked, so you know that the depth of the recursion is never more than V, the number of vertices in the graph. Now, how many times does the if (!marked[w]) statement execute? Well, assuming that you can retrieve the neighbors of a vertex in time directly proportional to its degree, then this statement executes twice for every edge E.

For a directed graph, the if (!marked[w]) statement would execute once for every edge E.

A similar argument can be made for Breadth First Search:

void bfs(Graph g, int s) { Queue<Integer> q = new Queue<Integer>(); marked[s] = true; q.enqueue(s); while (!q.isEmpty()) { int v = q.dequeue(); for (int w : g.adj(v)) { if (!marked[w]) { edgeTo[w] = v; marked[w] = true; q.enqueue(w); } } } }

The queue contains marked vertices. As each one is dequeued, its neighbors are checked; if any of them are unmarked, they are added to the queue. Thus once a vertex is marked it won’t be added back into the queue, which means the dequeue method is called no more than V times. In an undirected graph the inner if (!marked[w]) statement executes twice for every edge E in the graph.

1.3.3 An aside on random graphs

Construct a random undirected graph with N vertices as follows. Choose a probability, p, between 0 and 1. For each of the N*(N-1)/2 possible edges, add the edge to the graph with probability p. An independent decision is required for each edge.

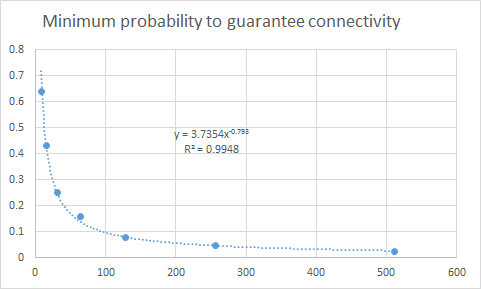
You want to guarantee that the graph is connected. This is a well-studied domain in theoretical computer science. Consider the following chart (computed from algs.days.day23.RandomConnectedGraphs):

Figure 1:

In this figure we used a modified binary search to try to identify the lowest probability which would guarantee that 200 random graphs (of size N) would remain connected.

Here is another way of presenting the same information. A series of 1,024 random graphs were constructed with p=0.001 to p=0.009 and the table shows the count of connected graphs for each (N, p). As you can see, for any given probability p – no matter how small – you could guarantee connectivity if you just increased the size of N.

N 0.001 0.002 0.003 0.004 0.005 0.006 0.007 0.008 0.009 8 0 0 0 0 0 0 0 0 0 16 0 0 0 0 0 0 0 0 0 32 0 0 0 0 0 0 0 0 0 64 0 0 0 0 0 0 0 0 0 128 0 0 0 0 0 0 0 0 0 256 0 0 0 0 0 0 0 0 0 512 0 0 0 0 0 0 0 0 9 1024 0 0 0 0 3 112 466 768 927 2048 0 0 16 588 952 1015 1023 1024 1024 4096 0 337 1003 1024 1024 1024 1024 1024 1024

Upon reflection, this might not be that surprising. After all, p is a fixed probability, and there are N*(N-1)/2 edges, so eventually, the sheer total number of edges will guarantee that the graph is connected.

Welcome to the field of asymptotic analysis...

1.4 Major concerns

We started with Sedgewick’s Tilde expressions to rapidly approximate the execution performance of an algorithm, or to compute the number of times a key function (such as compareTo) executed. We then moved to a more loose description, I called "Order of Growth".

The goal was to evaluate the worst case behavior that would result for an algorithm and to classify the algorithm into a well known performance family. We have seen several of these families to date. We now can classify their order of growth (in the worst case) using the following notation:

Constant: O(1)– Time to complete is independent of the size of the data
Logarithmic: O(log n) – Time to complete is directly proportional to the log2 of the size of the data
Linear: O(n) – Time to complete is directly proportional to the size of the data
Linearithmic: O(n log n) – Time to complete is directly proportional to the size of the data times the log2 of the size of the data
Quadratic: O(n2) – Time to complete is directly proportional to the square of the size of the data
Cubic: O(n3) – Time to complete is directly proportional to the cubic of the size of the data
Polynomial: O(nk) – Time to complete is directly proportional to some constant power of the size of the data
Exponential: O(kn) – Time to complete is directly proportional to a fixed constant raised to a power directly proportional to the size of the data

But what does this terminology mean? we need to turn to asymptotic complexity to answer that question:

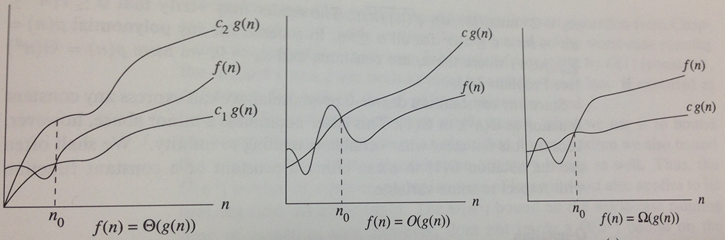
The above picture has a curve f(n) that represents the function of interest. At various times in this course, we have used this for a number of investigations:

Number of array inspections.
Number of times two object are compared with each other.
Number of times two values are exchanged during a sort.

We are increasingly interested in the performance of the overall algorithm, that is, instead of focusing on a single key operation, we want to model the full behavior so we can come up with a run-time estimate for completion.

The value n represents, typically, the problem size being tackled by an algorithm. As you can see, the value of f(n) changes over time, increasing when n increases. Here, n is the problem size.

The goal is to classify the rate of growth of f(n) and we use a special notation for this purpose, which looks awkward the first time you see it.

There are three notations to understand:

Lower Bound Ω(g(n)) – after a certain point, f(n) is always greater than c1*g(n).
Upper Bound O(g(n)) – after a certain point, f(n) is always smaller than c2*g(n).
Tight Bound Θ(g(n)) – after a certain point, f(n) is bracketed on the bottom by c1*g(n) and on the top by c2*g(n).

The phrase "after a certain point" eliminates some of the "noise" that occurs when working with small data sets. Sometimes even the most efficient algorithm can be outperformed by naive implementations on small data sets. The true power of an algorithm only becomes realized as the problem size grows to be sufficiently large. The constant n0 refers to the point after which the computations have stabilized. This value can never be uniquely determined, since it depends on the language used, the computer processor, its available memory, and so on. However, we define that it must exist (and it can be empirically determined for any algorithm should one wish to).

Note: We can use Ω(), Θ() and O() to refer to best case, average case, and worst case behavior. This can be a bit confusing. The whole point is to classify an asympotic upper (or lower) bound.

That being said, the most common situation is to analyze the worst case analysis. Since this is so common, most of the time it is understood. When I say, "Algorithm X is O(f(n))" I mean "the complexity of X in the worst case analysis is O(f(n))". This means that its performance scales similarly to f(n) but no worse than f(n).

Here is a statement that is always true: Everything that is Θ(f(n)) is also O(f(n)).

Once an algorithm is thoroughly understood, it can often be classified using the Θ() notation. However, in practice, this looks too "mathematical". Also it can’t be typed on a keyboard.

So what typically happens is that you classify the order of growth for the algorithm using O(g(n)) notation, with the understanding that you are using the most accurate g(n) classification.

To explain why this is necessary, consider someone who tells you they have a function to find the maximum value in an array. They claim that its performance is O(2n). Technically they are correct, because the rate of growth of the function (which is linear by the way) will always be less than some constant c*2n. However, there are other classifications that are more accurate, namely O(n).

And it is for this reason that all multiplicative and additive constants are disregarded when writing O() notations. Specifically, the constants matter with regard to the specific runtime performance of actual code on specific problem instances. Programmers can improve the code to reduce the constants, that is, making the program run faster in measurable quantities. However, theoretically, there are limits that programmers can achieve. And the overall order of growth, or rate of growth, is fixed by the design of the algorithm.

1.4.1 Order of Growth

Up until now, we were primarily concerned with order of growth analysis because that would help us to "eliminate the constants". Consider that you classifiy a function as requiring C(n) = 137*n2 comparison operations.

As the problem size doubles, then you would see C(2n) = 137*(2*n)2 comparisons. If you divide C(2n)/C(n) then the result eliminates the constants, resulting in 4. This is the hallmark of a quadratic behavior – when the problem size doubles, the result is a 4-fold increase.

We need to make one final comment on additive constants. If C(n) = 85*n + 1378, then C(2n) = 85*2*n + 1378. As you can see from the following table, ultimately the factor of n overwhelms the constant 1378. In fact, regardless of the magnitude of the constant, it will be overwhelmed by n once the size of the problem grows big enough.

n 85n+1378 C(2n)/C(n) 2 1548 4 1718 1.109819121 8 2058 1.19790454 16 2738 1.330417881 32 4098 1.496712929 64 6818 1.663738409 128 12258 1.797887944 256 23138 1.887583619 512 44898 1.940444291 1024 88418 1.96930821 2048 175458 1.984414938 4096 349538 1.992146269 8192 697698 1.996057653 16384 1394018 1.998024933 32768 2786658 1.999011491 65536 5571938 1.999505501

1.5 Master Theorem

We have seen a number of recurrence equations in this course, which are of the following form:

T(n) = aT(n/b) + f(n)

There are a number of special cases that can be handled by this theorem.

1.5.1 Find maximum recursively

We have already seen this algorithm for finding the maximum value in an array of N elements.

static Comparable largest (Comparable[] a, int lo, int hi) { if (hi <= lo) { return a[lo]; } int mid = lo + (hi - lo)/2; Comparable maxLeft = largest (a, lo, mid); Comparable maxRight = largest (a, mid+1, hi); if (less(maxLeft, maxRight)) { return maxRight; } else { return maxLeft; } }

When computing the number of comparisons used in this function, that can be described by

C(N) = 2*C(N/2) + 1

If you assume n is a power of 2 (to simplify the argument) then

C(N) = 2k*C(N/2k) + 2k-1 + 2k-2 + ... + 1

Note that C(N) = 0 and if you expand this out you get:

C(2n) = 2n-1 + 2n-2 + ... + 1

which equals N-1

From the original statement of the recurrence, however, this result could have been determined.

The master theorem declares how to compute these results without carrying out the telescoping process.

In particular, let a >= 1 and b > 1 be constants, and let f(n) be a function. Now define T(n) on the non-negative integers by the recurrence

T(n) = aT(n/b) + f(n)

And we interpret n/b to be either floor(n/b) or ceiling(n/b) as appropriate. We are trying to find the asymptotic bound for T(n) as n grows.

The key intuition is comparing f(n) with regards to nlogb(a). That is, you divide problem of size n into sub-problems of size n/b and then you perform a of them. When a < b, logb(a) < 1. However, if you perform a > b subproblems, then you will eventually begin to pay the cost, and you have to account for it.

In the recursive maximum computation, a = b = 2, which is a common case. That is,

T(n) = 2*T(n/2) + f(n)

Note that logb(a) in this case is log2(2) which is 1. So in this common case, what are the possible results?

if f(n) = O(nx) where x < 1, then T(n) = Θ(n).
if f(n) = Θ(n), then T(n) = Θ(n log n).
if f(n) = Ω(nx) where x > 1, and if a*f(n/b) <= c*f(n) for some c < 1, T(n) = Θ(f(n)).

*whew*

Why does this matter?

Well, if you found a recurrence of the form:

T(n) = 2*T(n/2) + Ω(n log n)

then you know that T(n) = Θ(n log n).

Ask yourself why the recursive functions don’t have additional work that requires sorting of the results? The reason is simply that the extra work performed during the recursion cannot be ignored and it will eventually build up to overwhelm the benefit of splitting the problem recursively.

You can use this same formula to compute the performance cost of the three-way merge sort which subdivided a problem into three sub-problems (thus, b=3 and a=3 also).

1.6 Other complexity families

There is a class of problems in computer science that have defied any efficient solution in a reasonable amount of time. These are known as the NP-Complete problems.

One example is called the "Hamiltonian Cycle" problem. Given an undirected (or directed) graph, compute a path that visits every vertex in the graph exactly once and then returns to the starting vertex.

While this problem looks very similar to the check whether a graph is connected, it cannot be solved without generating all possible paths. I will wave my hands for a bit and suggest that the number of possible paths in an undirected graph is proportional to N!

You can try your hand on sample random graphs in the HamiltonianCycle code example. This is similar in structure to the anagram solver, since it tries all possible paths.

1.7 Summary

You can find numerous online resources about the Big O notation. Here is one convenient one that I have found:

The Big-O Cheat Sheet