CS 2223 Apr 19 2018

Lecture Path: 22
Back Next

Expected reading: pp. 566-583
Daily Exercise:
Classical selection: Beethoven Symphony No 5 in C minor (1804-1808)
Musical Selection: Los Del Rio: Macarena (1996)

When you point your finger at someone, there are three pointing back at you.
Anonymous

1 Directed Graphs and Associated Algorithms

1.1 Quick Handouts update from Apr 19 2018

In the handout, I had the following code, which has typo on line 07

01 // depth first search from v 02 void dfs(int v) { 03 marked[v] = true; 04 for (int w : G.adj(v)) { 05 if (!marked[w]) { 06 edgeTo[w] = v; 07 dfs(G, w); 08 } 09 } 10 }

Line 07 should read:

07 dfs(w);

otherwise it would be calling the other method, which is incorrect. I’ve updated in the handout that is uploaded to the git repository.

1.2 Helper video for HW4 in setting up classes

I put together a video showing how to copy the algs.hw4.expr classes into your HW4 project. Hope this helps you set things up properly.

Find the video in the Echo360 area of the Canvas web site.

1.3 Directed Graph structure

Any discussion of graphs always start with undirected graphs. Over the next few lectures we are going to expand the domain to introduce some standard extensions.

Today we will discuss directed graphs or digraph for short. A digraph is a set of vertices and a collection of directed edges. Each directed edge connects an ordered pair of vertices in a specific direction.

The first difference between a graph and a digraph is that a digraph may have up to two different edges between the same pair of vertices. Specifically, the edge (v, w) is different from (w, v).

Many of the concepts introduced in the past few lectures apply here. Note that the Digraph implementation has only one line changed, namely, within the addEdge method. This method only updates a single Bag in the storage.

1.4 DFS over a Digraph

Naturally it makes sense to consider searching digraphs in the same manner as performed over graphs. This is shown on page 571.

With directed graphs, there are more complex traversals through a graph, and we are no longer simply interested in whether the entire graph is "connected" between any two vertices. Rather, we are interested in specific reachability from individual vertices.

Note that it is not necessary for you to create a new class, DirectedDFS, to use for the directed search. Indeed, you can place the recursive dfs method in any class, and then make the marked arrays local fields of that class.

Depth First Search on digraphs works identically to undirected graphs. Here is what the code looks like:

/** Compute DFS from source vertex. */ public DirectedDFS(Digraph G, int s) { marked = new boolean[G.V()]; dfs(G, s); } /** Compute DFS from collection of sources. */ public DirectedDFS(Digraph G, Iterable<Integer> sources) { marked = new boolean[G.V()]; for (int v : sources) { if (!marked[v]) dfs(G, v); } } void dfs(Digraph G, int v) { marked[v] = true; for (int w : G.adj(v)) { if (!marked[w]) dfs(G, w); } }

As you can see, the code is nearly identical. The only change is that you only visit neighbors in the direction of an edge.

One of the fundamental questions that arise with directed graphs is to identify cycles in a graph. Recall that a cycle is (p. 567), "a directed path with at least one edge whose first and last vertices are the same."

We can convert the mechanics of Depth First Search into a cycle detector:

1.5 Directed Acyclic Graphs (DAGs)

When executing DFS, you recall that you don’t extend the depth first search to marked vertices. Well, can you use this observation to detect cycles? Consider the following graph.

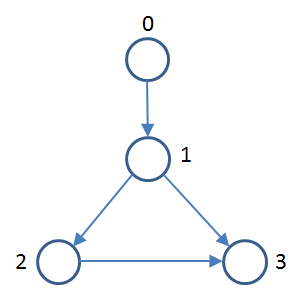
And using the recursive DFS above, you would visit 0 to 1 to 2 and then to 3. How can you detect when there is a cycle? You need some more bookkeeping.

See handout.

Specifically, in the above graph, using dfs visit from vertex 0 would recursively invoke dfs(1) and then dfs(2) and finally dfs(3). The function stack would look list this:

dfs(0) ; check 1 dfs(1) ; check 2 [then 3] dfs(2) ; check 3 dfs(3) ; no outgoing neighbors

At this point, the recursion begins to unwind, all the way back to:

dfs(0) ; check 1 dfs(1) ; [done with 2] now checking 3

When visiting 3 (a previously marked vertex) there is a cycle. We need a way to determine this.

The solution is to maintain an extra array inStack which determines which vertices are "actively being pursued in the depth first recursion from the original source vertex." If you revisit a previously marked vertex that is still under active investigation, then you have found a cycle. This code is shown below:

void dfs(Digraph G, int v) { onStack[v] = true; marked[v] = true; // terminate once a cycle has been found if (hasCycle() != null) { return; } for (int w : G.adj(v)) { if (!marked[w]) { edgeTo[w] = v; dfs(G, w); } else { // might be a cycle if w is still on stack. // Construct cycle on demand if (onStack[w]) { cycle = new Stack<Integer>(); for (int x = v; x != w; x = edgeTo[x]) { cycle.push(x); } cycle.push(w); cycle.push(v); } } } onStack[v] = false; // done }

We can test out this class using sample graphs. Does the following graph have a cycle anywhere?

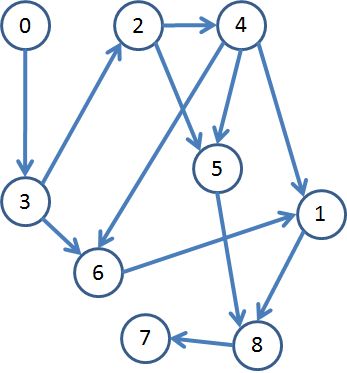
% java algs.days.day22.DirectedCycle day22.txt

Let’s review this problem using a handout.

1.6 Topological Sort

We now can detect when a directed graph is acyclic; often called DAGs, these are commonly used to represent any number of problems. Here is one problem, known as Topological Sort.

Given a digraph, produce a linear ordering of its vertices such that for every directed edge uv (from vertex u to vertex v), u comes before v in the ordering.

We can use Depth First Search to determine this ordering. The key is to reflect on the final step in dfs which marks onStack[v] as false. This line executes when the recursion is ’unwinding’ back to an earlier vertex to try to attempt a different search direction.

It is exactly at this point that you know vertex v is a dead-end of sorts. That is, it is impossible to reach other vertices in the graph through this direction. Well, isn’t this exactly what we want to determine when it comes for topological sorting?

The only trouble is that we are unwinding and visiting vertices in reverse order from how they should appear in a toplogical ordering.

For example, if there are three vertices – A, B and C, with an edge from (A,B) to signal A must complete before B, and an edge from B to C to signal B must complete before C, then we know C must be the LAST in the topological ordering. When issuing dfs(A) it terminates at C and during the unwinding of the recursion, the onStack[v]=false statement executes for C, B and then A.

void dfs(Digraph G, int v) { marked[v] = true; for (int w : G.adj(v)) { if (!marked[w]) { edgeTo[w] = v; dfs(G, w); } } // amazingly, store vertex in order by reverse postorder. reversePost.push(v); }

The final processing step is to ensure that the entire graph is visited. It may be the case that not every vertex is reachable from vertex 0, because of the nature of the directed edges.

Thus in the constructor to DirectedDFS search, we iterate over all unmarked vertices in the graph. The first dfs search is launched from vertex 0; thereafter, any unmarked vertex becomes the point at which a new dfs search is initiated. This continued until all vertices in the graph are marked.

public DirectedDFS(Digraph G) { marked = new boolean[G.V()]; edgeTo = new int[G.V()]; reversePost = new Stack<Integer>(); for (int v = 0; v < G.V(); v++) { if (!marked[v]) { dfs(G, v); } } }

This completes the discussion of Topological sort.

% java algs.days.day22.Topological day22-dag.txt 0 3 2 4 5 6 1 8 7

1.7 Daily Exercise

Is it possible to convert DirectedCycle into a non-recursive solution? Yes, but the code is more complicated. Think about it, and I will post in tomorrow’s code base.