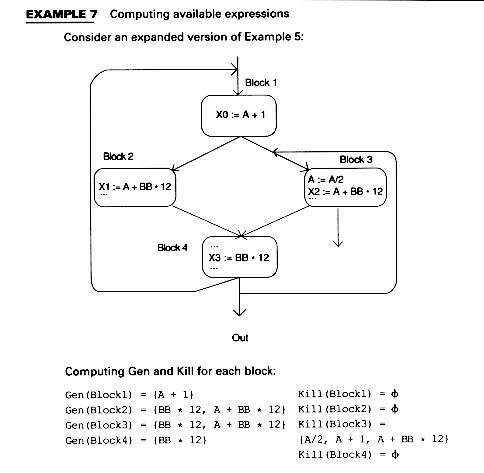
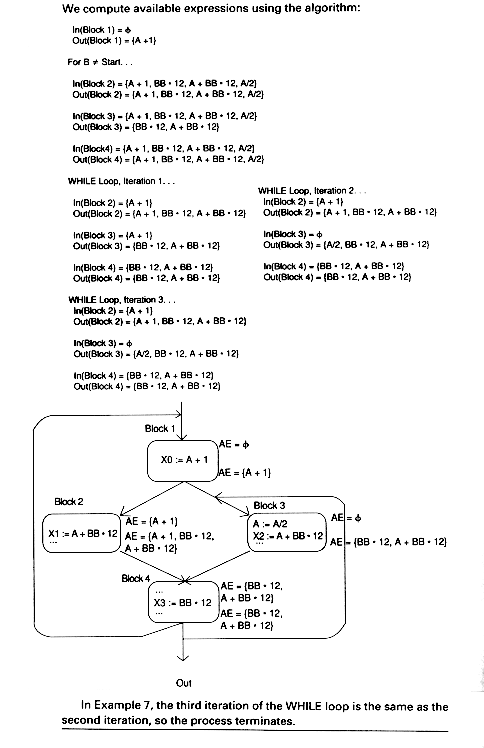
Computing Available Expressions

Use of Available Expressions

Finding available expressions is similar to finding reaching definitions. Again we use the variables In(B), Out(B). We use the term A op B to mean any expression, even one which has more that one op, as in A + BB * 12.

Transfer Function Rules

For available expressions, the variables Kill(B) and Gen(B) are defined as follows:

Kill(B) = {the expressions X op Y in the program such that X or Y is defined in B},

that is, X or Y occurs on the left of an assignment statement or in a read statement.

Gen(B) = {the expressions X op Y computed in B, with no subsequent definitions of X or Y in B}

EXAMPLE 6 Gen and Kill sets for a block B

Consider the following statements in some basic block B

A := B + C
X := Y - Z
B := X + Y
X := A * B
In Example 6, Gen(B)={Y-Z, A*B}. Kill(B)={B+C,X+Y} plus other expressions such as, say, X + Q, since X is on the left-hand side of an assignment in B.

---

Transfer Equation

We have "rigged" the definition of Gen and Kill for available expressions so that the equation of Out is the same as that for reaching definitions

Out(B) = (In(B) - Kill(B)) Gen(B)

Confluence Rule

An expression is available at a point only if it is computed on all preceding paths:

In(B) = Out(P)

^{P Pred(B)}

We initialize In(start) = even though it may have predecessors.

Solving the Equations

This time we want the largest solution since we don't want to rule out an expression unless we find a path along which it is unavailable. Thus, we will initialize the In and Out sets to make every expression available and then eliminate expressions that are not readily available. Here, we throw things out (via intersection) the way reaching definitions threw things in (via union).

Algorithm

Available Expressions

 In(Start) = 
 Out(Start) = Gen(Start)
 FOR B < > Start DO
   In(B) = All Expressions in program
   Out(B) = (In(B) - Kill(B))  Gen(B)
 ENDFOR
 WHILE there are changes DO
   FOR B < > Start DO
     In(B) =  Out(P)
           P   Pred(B)

     Out(B) = (In(B) - Kill(B))  Gen(B)
   ENDFOR
 ENDWHILE