9.2.3 The Iterative Method for Solving Data Flow Equations

We will develop an iterative algorithm for reaching definitions. The reader need not despair that there will be a new algorithm for every data flow problem, however. Only minor changes need to be made to the equation to solve the other problems.

We start by assuming that what comes out of a block consists of the definitions generated in them.

We then repeatdly visit the nodes, applying the confluence rules to get new In's and the transfer rules to get new Out's. By pred(B), we mean the immediate predecessors.

Algorithm

Reaching Definitions

 FOR each block B, DO
   In(B) = 
   Out(B) = Gen(B)
 ENDFOR
   WHILE there are changes DO
     FOR each block B DO
       In(B) =  Out(P)
             ^{P  Pred (B)}
       Out(B) = (In(B) - Kill(B))  Gen(B)
     ENDFOR
   ENDWHILE

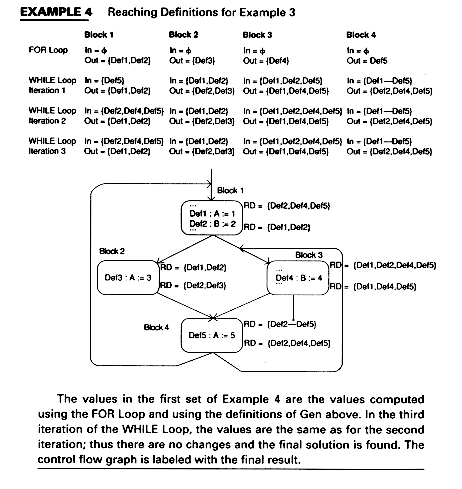
The values in the first set of Example 4 are the values computed using the FOR Loop and using the definitions of Gen above. In the third iteration of the WHILE Loop, the values are the same as for the second iteration; thus there are no changes and the final solution is found. The control flow graph is labeled with the final result.