Defining a Loop

Headers

Dominators

Natural Loops

Depth-First Order and Depth-First Spanning Trees

Finding Natural Loops Efficiently

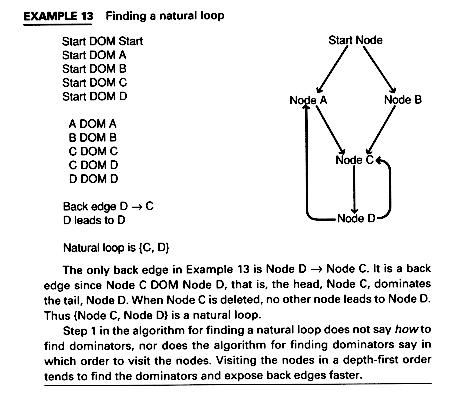
8.6.4 Natural Loops

We use dominators to find loops. Since loops contain a cycle, and a header dominates all the nodes in a loop,

    there must be a least one arc entering the header from a node in the loop

For this reason, we search for an arc whose head dominates its tail. This is called a back edge. Loops must have a back edge.

The natural loop of the back edge is defined to be the smallest set of nodes that includes the back edge and has no predecessors outside the set except for the predecessor of the header. Natural loops are the loops for which we find optimizations.

    Algorithm

    Finding the nodes in a natural loop

    FOR every node n, find all m such that n DOM m
    FOR every back edge th, i.e., for every arc such that h DOM t, construct the natural loop:

      Delete h and find all nodes which can lead to t
    These nodes plus h form the natural loop of th