cs2223 Summing Factors

[WPI] [cs2223] [cs2223 text] [News] [Notes] [Recurrence]

cs2223, D97/98 Summing Factor Solutions

The class of first-order, non-homogeneous, linear recurrence relations can usually be solved by means of the summing factor solution, which is closely related to the integrating factor solution for first-order differential equations.

General Solution

Assume the recurrence relation can be written in this form:

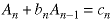
A(n) + b(n)*A(n-1) = c(n)

where the b_n and c_n are functions of n. Here are two examples:

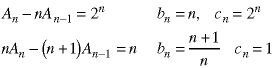
A(n) - n*A(n-1) = 2^n, b(n) = n and c(n) = 2^n; n*A(n) - (n+1)*A(n-1) = n, b(n) = (n+1)/n and c(n) = 1

Then the solution is.

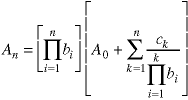
A(n) = product(i=1 -> n; b(i)) * (A(0) + sum(k=1->n; c(k) / product(i=1->k; b(i))))

Where A_n is the initial condition. Note that none of the coefficients b_n can be zero or the denominator inside the summation becomes zero and the solution may not exist.

Examples

If we assume A0=0, the solution to the first recurrence relation above is:

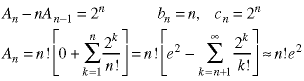
A(n) - n*A(n-1) = 2^n, b(n) = n and c(n) = 2^n; A(n) = n! * (0 + sum(k=1 -> n; 2^k / n!) = n! * (e^2 - sum(k=n+1 -> infinity; 2^k / k!)))) approx= n!e^2

The approximation applies for large values of n.

Assuming, again, assume A0=0, the solution to the second recurrence relation above is:

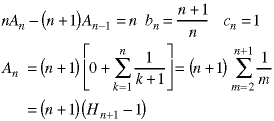
n*A(n) - (n+1)*A(n-1) = n * b(n) = (n+1)/n and c(n) = 1; A(n) = (n+1) * (0 + sum(k=1->n; 1/(k+1)) = (n+1) * sum(m=2 -> n+1; 1/m) = (n+1) * (H(n+1) -1)

Note the use of Hn, the Harmonic series, which is discussed in Class 4.

The attached Excel spreadsheet shows that the first few terms of these solutions are correct. A zip versionis attached for those whose browsers experience difficulty when downloading Excel spreadsheets.