cs2223 Solving Recurrence Relations

[WPI] [cs2223] [cs2223 text] [News] [Notes] [Recurrence] [Solving]

cs2223, D97/98 Solving Recurrence Relations - Step 4

Eliminate the Undetermined Coefficients

The final step is the elimination of the undetermined coefficients, which we have been carrying around since Step 2 - they came from the homogeneous solution. We do this by using initial or boundary conditions to evaluate the coefficients.

Recall that we got one undetermined coefficient from each order in the homogeneous solution: a first-order recurrence relation produces one undetermined coefficient; a second-order relation produces two, etc. Thus we need one initial condition for each order in the recurrence relation.

Note, a numerical demonstration that we got the right answers is contained in the attached Excel spreadsheet. A zip version is attached for those whose browsers have difficulty downloading Excel files.

Example 4_1, based on Example 3_1

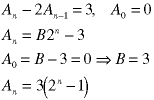
A(n) - 2*A(n-1) = 3, A(0) = 0; A(n) = B*2^n -3; A(n) = B - 3 = 0 -> B = 3; A(n) = 3*(2^n -1)

Example 4_2, based on Example 3_2

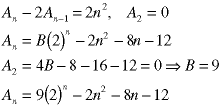
A(n) - 2*A(n-1) = 2*n^2, A(2) = 0; A(n) = B*2^n - 2*n^2 - 8*n - 12; A(2) = 4*B - 8 - 16 - 12 = 0 -> B = 9; A(n) = 9*2^n - 2*n^2 - 8*n - 12

Note that this Example used an initial condition at n=2, not zero.

Example 4_3, based on Example 3_3

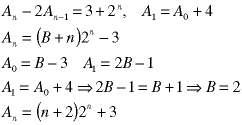
A(n) - 2*A(n-1) = 3 + 2^n; A(1) = A(0) + 4; A(n) = (B + n)*2^n -3; A(0) = B - 3, A(1) = 2*B - 1; A(1) = A(0) + 4 -> 2*B -1 = B + 1 -> B = 2; A(n) = (n + 2)*2^n + 3

Note the form of the initial condition. No explicit values were given, only the relationship between two starting valuees.

Example 4_4, based on Example 3_4

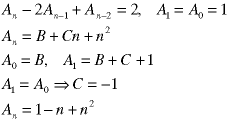
A(n) - 2*A(n-1) + A(n-2) = 2, A(1) = A(0) = 1; A(n) = B + C*n + n^2; A(0) = B, A(1) = B + C + 1; A(1) = A(0) -> C = -1; A(n) = 1 - n - n^2

Example 4_5, based on Example 3_5

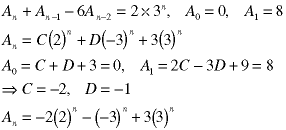
A(n) + A(n-1) - 6*A(n-2) = 2*3^n, A(0) = 0, A(1) = 8; A(n) = C*2^n + D*(-3)^n + 3*3^n; A(0) = C + D + 3 = 0, A(1) = 2*C - 3*D + 9 = 8 -> C = -2, D = -1; A(n) = -2*2^n - (-3)^n + 3*3^n

Example 4_6, based on Example 3_6

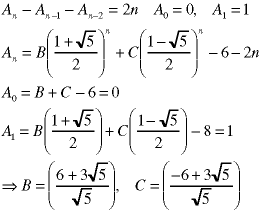
A(n) - A(n-1) - A(n-2) = 2*n, A(0) = 0, A(1) = 1; A(n) = B*((1+sqrt(5))/2)^n + C*((1-sqrt(5))/2)^n - 6 - 2*n; A(0) = B + C - 6 = 0; A(1) = B*((1+sqrt(5))/2) + C*((1-sqrt(5))/2) - 8 = 1 -> B = ((6+3*sqrt(5))/sqrt(5)), C = ((-6 + 3*sqrt(5))/sqrt(5))

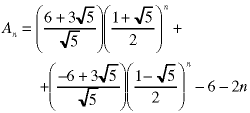
A(n) = ((6 + 3*sqrt(5))/sqrt(5)) * ((1+sqrt(5))/2)^n + ((-6+3*sqrt(5))/sqrt(5)) * ((1-sqrt(5))/2)^n -6 -2*n

Note that the values of this sequence are real for integral values of n.

Example 4_7, based on Example 3_7

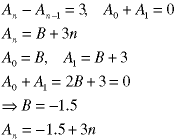
A(n) - A(n-1) = 3, A(0) + A(1) = 0; A(n) = B + 3*n; A(0) = B, A(1) = B+3; A(0) + A(1) = 2*B + 3 = 0 -> B = -1.5; A(n) = -1.5 + 3*n

Example 4_8, based on Example 3_8

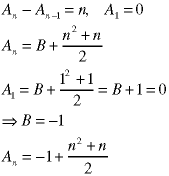
A(n) - A(n-1) = n, A(1) = 0; A(n) = B + (n^2 + n)/2; A(1) = B + (1^2 + 1)/2 = B + 1 = 0 -> B = -1; A(n) = -1 + (n^2 + n)/2

Example 4_9, based on Example 3_9

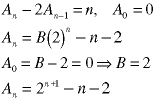
A(n) - 2*A(n-1) = n, A(0) = 0; A(n) = B*2^n - n - 2; A(0) = B - 2 = 0 -> B = 2; A(n) = 2^(n+1) - n - 2