cs2223 Classifying Recurrence Relations

[WPI] [cs2223] [cs2223 text] [News] [Notes] [Recurrence]

cs2223, D97/98 Classifying Recurrence Relations

There are only a few types of recurrence relations which can be solved in closed form - which means any term in the sequence can be evaluated by plugging numbers into an equation instead of having to calculate the entire sequence. Classifying the recurrence relation helps to decide which, if any, techniques can be used to solve it.

Here is a generic recurrence relation, consisting of a sequence of terms A_n.

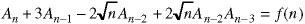
A(n) + 3*A(n-1) - 2*sqrt(n)*A(n-2)*A(n-3) = f(n)

The right side f(n), is some function of n, the number of A_n in the sequence. In the standard form, the right side of a recurrence relation can contain any function of n, but must not contain any of the A_n.

There are four characteristics of the recurrence relation to note.

Homogeneous or non-homogeneous

A recurrence relation is homogeneous if the right side is zero. The above recurrence relation is non-homogeneous, but this one is homogeneous.

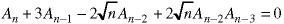
A(n) + 3*A(n-1) - 2*sqrt(n)*A(n-2) + 2*sqrt(n)*A(n-2)*A(n-3) = 0

Linear or non-linear

A recurrence relation is linear if there are no products or powers of the sequence elements. The above recurrence relations are non-linear. These recurrence relations are linear.

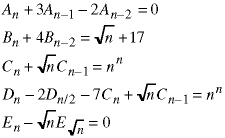
A(n) + 3*A(n-1) - 2*A(n-2) = 0; B(n) + 4*B(n-2) = sqrt(n) + 17; C(n) = sqrt(n)*C(n-1) = n^n; D(n) - 2*D(n/2) - 7*C(n) + sqrt(n)*C(n-1) = n^n; E(n) - sqrt(n)*E(sqrt(n)) = 0

These recurrence relations are non-linear.

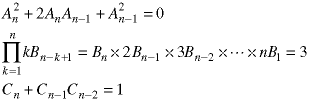
(A(n))^2 + 2*A(n)*A(n-1) + (A(n-1))^2 = 0; product(k=1->n; k*B(n-k+1)) = B(n) * 2*B(n-1) * 3*B(n-2) * ... * n*B(1) = 3; C(n) + C(n-1)*C(n-2) = 1

Order of the Recurrence Relation

The order of the recurrence relation is the number of steps along the sequence from the first to the last members in the relation.

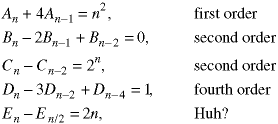
A(n) + 4*A(n-1) = n^2 is first order; B(n) - 2*B(n-1) + B(n-2) = 0 is second order; C(n) - C(n-2) = 2^n is second order; D(n) - 3*D(n-2) + D(n-4) = 1 is fourth order; E(n) - E(n/2) = 2*n is WHAT?

The last recurrence relation does not have a constant order. That complicates the solution.

Constant versus non-constant coefficients

We make a distinction between recurrence relations in which the coefficients which multiply the sequential terms are constant, such as these

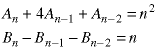
A(n) + 4*A(n-1) + A(n-2) = n^2; B(n) - B(n-1) - B(n-2) = n

and those recurrence relations in which the coefficients are not constant - they vary with n, such as these.

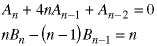
A(n) + 4*n*A(n-1) + A(n-2) = 0; n*B(n) - (n-1)*B(n-1) = n

So what?

There are two classes of recurrence relations which are always solvable so it is important to recognize them.

First-order, non-homogeneous, linear recurrence relations in which the coefficients are never zero.
Any constant order linear recurrence relation with constant coefficients which are homogeneous or whose right sides can be expressed as the product of polynomials in n and constants to the n-th power.

The solution techniques for these two classes of recurrence relation are discussed in detail in the Recurrence page. Other recurrence relations are generally harder to solve, although a few special cases have been solved.