cs2223 Exam 3 Solution

[WPI] [cs2223] [cs2223 text] [News] [Syllabus] [Exams] [Exam 3]

cs2223, D97/98 Exam 3 Solution

Question 3.1

This is Newton's method for finding the square root of a number. It starts when the error is about n and ends when the error is 2^-20 and the error is roughly halved during each step. Thus the order is approximately:

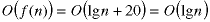
O(f(n)) = O(lg(n) + 20) = O(lg(n))

This is verified in the attached script. Note when n is a perfect square that the approximately 20 additional steps are not performed.

Question 3.2

The function calls itself recursively twice with n-1 and it performs two subtractions and two additions. The recurrence relation for the number of additions or subtractions is:

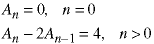
A(n) = 0, n = 0; A(n) - 2*A(n-1) = 4, n>0

The solution is:

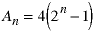
A(n) = 4*(2^n -1)

When n = 10⁵⁰, the answer is a very large number:

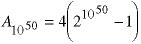
A(10^50) = 4 * (2^10^50 -1)

The attached script shows that this function produces the correct answer when n=20.

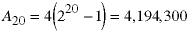
A(20) = 4 * (2^20 -1) = 4,194,300

Question 3.3

Use the algorithm from Section 8.1.1 of the text to calculate the binomial coefficient. The attached script shows that this function produces the correct answers - compare with the table in Section 8.6 of the text.

long int catalan(int number) // catalan number
	{ // uses pascal's triange; assume 0 <= n <= 20
	long int triangle[39][39] = {0}; // it never gets bigger than this
	int n, k; // see section 8.1.1 of the text
	for (n = 0; n < 39; n++) triangle[n][0] = 1;
	for (n = 1; n < 39; n++) // fill in pascal's triangle
		for (k = 1; k <= n; k++)
			triangle[n][k] = triangle[n-1][k-1] + triangle[n-1][k];
	return triangle[2*number - 2][number - 1] / number;
	} // end catalan()

The grading criteria are available. These are subject to interpretation by the grader. As we stated in class, our primary goal in the grading of these exams is consistency. If your intrepretation differs from the grader's and the grader has applied her/his criteria uniformly, then the grader's interpretation will prevail.