cs2223 Exam 3

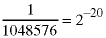
[WPI] [cs2223] [cs2223 text] [News] [Syllabus] [Exams]

cs2223, D97/98 Exam 3

Question 3.1

double unknown(double number, double guess, double increment)
   { 
   double error = guess * guess - number;
   double abs_error = error < 0 ? -error : error; // absolute value
   if (abs_error < 1.0 / 1048576.0) return guess; // close enough
   double inc2 = increment / 2.0; // new increment
   if (error > 0)
         return unknown(number, guess - inc2, inc2);// positive error
   else  return unknown(number, guess + inc2, inc2);// negative error
   } // end unknown()

Q1a). What does this function do? Explain in words.

Q1b). What is the order of this algorithm as a function of the number n if it is called with this statement:

double answer = unknown(n, n, n);

Note: This is not a perfect algorithm but it works reasonably well with n in the range 1 -> 1000. Also,

note that:

1/1048576 = 2^(-20)

Question 3.2

A very cautious person has written this function to double a number (it works). Everything is done twice, just to be cautious.

int doubledouble(int n) // double a number
   {
   extern int add_sub; // to keep track of additions/subtractions
   int answer;
   if (n <= 0) return 0;
   else
      {
      add_sub++; doubledouble(n-1); // do this twice
      add_sub++; doubledouble(n-1);
      add_sub++; answer = n + n; // do this twice, too
      add_sub++; answer = n + n;
      return answer; 
      }
   } // end doubledouble()

If your computer could handle really big ints, what number would be printed by these statements (note that n = 10⁵⁰) ? You don't have to write out the number - just show an equation for it.

int n = 100000000000000000000000000000000000000000000000000;
doubledouble(n);

Question 3.3

The Catalan number is defined in the text - page 280 - as:

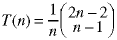
T(n) = C(2*n -2, n-1)/n where C(a,b) is the 'choose' or 'combinations' function, which tells how many ways a objects can be grouped into one group of size b and another of size a-b.

Write a complete, working, non-recursive, C or C++ function which calculates the Catalan number. Here is the function's prototype:

long int catalan(int n);

Note: "complete, working" means it can be compiled by g++ and it will work correctly. The Catalan numbers grow very quickly so, to fit the answer in a long int, you may assume n<=20.