[WPI] [cs2223] [cs2223 text] [News] [Syllabus] [Exams] [Exam 2] 

cs2223, D97/98 Exam 2 Solution

Question 2.1

The integer n is defined as even if there is an integer j such that

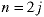
The integer m is defined as odd if there is an integer k such that

There are several proofs.

Direct Proof

Assume n is even. Then it's square is:

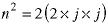
The number inside the parentheses is an integer (the domain of integers is closed under multiplication) so the square is even by the definition.

Assume m is odd. Then it's square is:

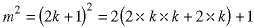
The number inside the parentheses is an integer (the domain of integers is closed under multiplication) so the square is odd by the definition.

These proofs are true for all integers so they are certainly true for all positive integers.

Indirect Proof

Assume n is even and its square is odd. Then there are two integers j and k related as follows:

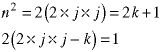
The number inside the parentheses is an integer (the domain of integers is closed under multiplication and subtraction) so the left side is even by definition. But the right side is odd by definition and no number is both odd and even so the assumption was wrong.

Assume m is odd and its square is even. Then there are two integers k and j related as follows:

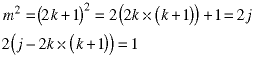
The number inside the parentheses is an integer (the domain of integers is closed under multiplication and subtraction) so the left side is even by definition. But the right side is odd by definition and no number is both odd and even so the assumption was wrong.

These proofs are true for all integers so they are certainly true for all positive integers.

Inductive Proof

The first positive even integer is:

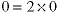
This is the basis step. Assume the statement is true for any postive even integer n (the inductive assumption). The square of the next even integer is:

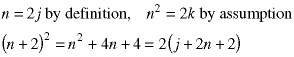
This number is even so the statement is true by induction.

The first positive odd integer is:

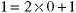
This is the basis step. Assume the statement is true for the postive odd integer m (the inductive assumption). The square of the next odd integer is:

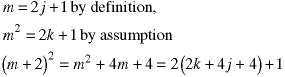
This number is odd so the statement is true by induction.

These proofs are true for all positive integers. Extension to negative integers would require additional proofs.

Question 2.2

The differences between a heap and a binary search tree are that the binary search tree has the additional requirement that the left child is greater than the right child and the heap has the additional requirement that everything is pushed as far left and up as possible. So the heap structure is a binary search tree structure. The only additional requirement is to swap the children, if necessary.

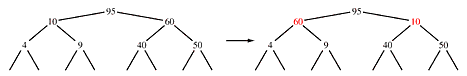
Such a swap cannot affect the relationship between the children and the parent (the parent is still larger than either) and connot affect the relationshop between the left child and it's children (the swap can only increase the value in the left node so the binary search tree property is still maintained), but it can affect the right child's relationship with it's children. So, perform a sift downward from the right child, as discussed in Class 9. These functions perform this algorithm.

void heap_to_bst(int the_size, int *the_array)
	{
	for (int look_here = 1, look_here < the_size / 2; look_here++)	
		{
		int left = look_here * 2; // index of left child
		int right = left + 1; // index of right child
		if ((right <= the_size) && (the_array[right] > the_array[left])) // swap them
			{
			swap_int(the_array[right],the_array[left]);
			sift(the_size, the_array, right); // sift down the right side
			}
		}
	return;
	} // end heap_to_bst()

void sift(int the_size, int *the_array, int look_here)
	{
	if (look_here > (the_size / 2)) return; // already at a leaf
	int left = look_here * 2; // index of left child
	int right = left + 1; // index of right child
	if ((right <= the_size) && (the_array[right] > the_array[left])) // swap right
		{
		if (the_array[right] > the_array[look_here])
			{
			swap_int(the_array[look_here], the_array[right]);
			sift(the_array, the_heap, right); // continue downward
			}
		}
	else // swap left
		if (the_array[left] > the_array[look_here])
			{
			swap_int(the_array[look_here], the_array[left]);
			sift(the_size, the_array, left); // continue downward
			}
	return;
	} // end sift()

void swap_int(int &x, int &y) { int temp = x; x = y; y = temp; return; }

Question 2.3

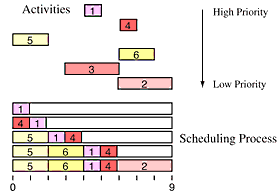
This is similar to the example in Class 12 - the case of "Fixed Deadlines with Varying Durations". The difference is that this time we want to print the shortest duration jobs first to maximize the amount charged.

• Sort the activities in increasing order of duration
• Within each group of activities with the same duration, sort the activities by increasing ending time
• Schedule activities from the top of the list to the bottom, avoiding overlaps. In each case, place the activities as early as posible in the schedule without pushing anything already in the schedule past its deadline.

The grading criteria are available. These are subject to interpretation by the grader. As we stated in class, our primary goal in the grading of these exams is consistency. If your intrepretation differs from the grader's and the grader has applied her/his criteria uniformly, then the grader's interpretation will prevail.

[cs2223 text] [News] [Syllabus] [Exams] [Exam 2]

Contents ©1994-1998, Norman Wittels
Updated 02Apr98