cs2223 Class 12

[WPI] [cs2223] [cs2223 text] [News] [Syllabus] [Classes]

cs2223, D97/98 Class 12

Scheduling

Greedy algorithms are often used to solve scheduling problmem. We looked at three similar schduling problems. In each case, note how the optimization criterion influences the algorithm

Fixed starting and stopping times

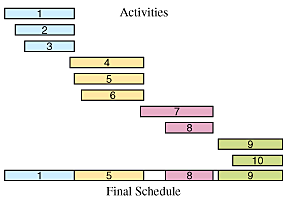
Consider the scheduling of activities which compete for a single resource and which have fixed beginning and ending times. An example would be scheduling of activities in Perreault Hall at WPI. Each activity - class, movie, exam, etc. - begins and ends at fixed times and none can be rescheduled to prevent overlap. If we want to maximize the use of the room, we can use this algorithm.

Sort the activities in increasing order of ending time
Within each group of activities with the same ending time, sort the activities by decreasing duration
Schedule activities from the top of the list to the bottom, avoiding overlaps

Figure showing graphically ten activities arranged as described

This algorithm always selects the first activity in the list, which may not provide the best possible overall optimization. Once that activity has been selected, the algorithm selects compatible (non-overlapping) activities in an optimal set (maximum use of the Hall). Also, this algorithm does what it is designed to do - maximize the amount o time the Hall is used - but it usually leaves some gaps during which the Hall is unused and it almost certainly leaves some people disappointed because some activities will not be scheduled. This algorithm is of order O(nlgn) because that is what is required to sort the activities. The actual scheduling is of order O(n) because each activity is looked at exactly once in building the schedule.

Fixed Deadlines with Varying Rewards

Another scheduling problem involves activities which all take the same length of time but which have different rewards associated with them. This is the problem described in Section 6.6.2 of the text. For example, suppose a physician treat patients in one-half appointments, but the fee depends on what each patient's health insurance plan will pay. What schedule will maximize the physician's income? The optimal scheduling algorithm is:

Sort the activities in decreasing order of reward
Within each group of activities with the same reward, sort the activities by increasing ending time
Schedule activities from the top of the list to the bottom, avoiding overlaps. In each case, place the activities as early as posible in the schedule without pushing anything already in the schedule past its deadline.

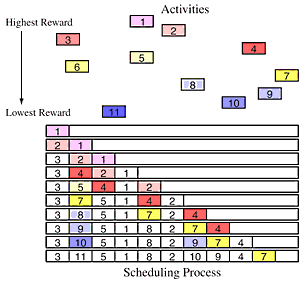
Image which graphically depicts the above algorithm

The color has been removed from each activity as it becomes "frozen" - it has already moved to as late a position as possible. Every activity in this example has been scheduled, except activity 6, which cannot be scheduled without removing activity 3. And, we cannot do that because activity 3 has a higher reward. The order of the algorithm is the same as the order of the sorting: O(nlgn).

Fixed Deadlines with Varying Durations

In another variation of the last scheduling problem, assume activities have fixed deadlines but the duration varies. We want to maximizie the time that activities are being performed. For example, assume the fees a radio station pays a performer are the same - independent of the length of the songs. The station would like to play as few songs as possible, while filling up as much of the program time as possible. If we add the further restriction that there is a deadline by which each song must be played, we can assign a "reward" which is equal to the length of the song, since the minutes per dollar is greatest for long songs. Then this problem is the same as the last one and can be solved using the same algorithm.

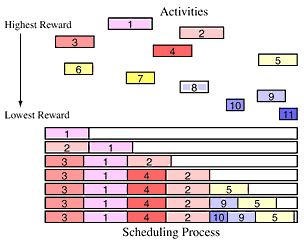
Graphical illustration of the algorithm

The time slots were not "frozen" because it is sometimes possible to interleave very short activities. For example, if activity 11 had been as short at the free time at the end of the schedule, it could have been placed at the beginning, in front of activity 3, without moving any of the other activities past their deadlines. This algorithm is of order O(nlgn).

Varying Durations but no Deadlines

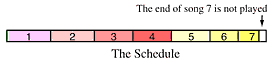
If we look at the last problem but without deadlines - the songs can be played in any order - then this just becomes the knapsack problem, section 6.5 in the text. Select songs in order of decreasing length and chop off whatever of the last song doesn't fit:

Graphical illustration of the algorithm

Minimum Spanning Trees

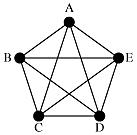
An undirected graph consists of labeled nodes and edges with lengths. A graph with n nodes can have this many edges:

sum(k=1->n-1; k) = n*(n-1)/2

This graph has five nodes and up ten edges

Image showing five nodes arranged as a pentagon with all ten edges included

A spanning tree is a set of edges which connects every node without circuits or cycles or loops (alternative terms). A graph with n nodes will have n-1 nodes in a spanning tree. Here are two possible spanning trees.

Figure showing two spanning trees for the five nodes

If the length or cost of each edge is known, we want to find the minimum spanning tree - the one whose lengths total to the smallest possible number. For example, if the nodes and edges represents cities and roads, the minimum spanning tree is the lowest cost network of roads which connects all cities.

Assume the costs or lengths of the edges - in increasing order - are:

BE, AD, BD, DE, BC, AB, CE, AE, AC, CD

We looked at two algorithms which produce the same results.

Kruskal's Algorithm

This is a recursive algorithm which assumes the edge list has been sorted in increasing order of length:

Start at the beginning of the list
Select the first unselected edge which connects two sets of connected nodes which are not connected to each other. This is how we avoid loops or cycles.

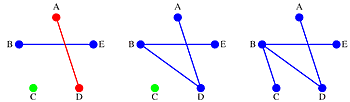
When we begin, all of the nodes are connected to themselves but to no other nodes. Select the first edge, BE. This creates the new connected set with the nodes B and E. Sets of connected nodes are shown in different colors.

Figure showing a link between two nodes

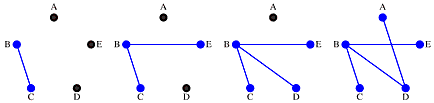
Next we add edge AD, then BD and then BC to produce the spanning tree. Edge DE is bypassed because adding it would create the circuit BDE.

Figure showing a spanning tree growing link-by-link until complete

Prim's Algorithm

Sort the edge list in increasing order of length:

Pick any node, for example node C.
Recursively start at the beginning of the edge list and add the first unselected edge which adds a new node to the connected set without creating any circuits.

Figure showing the growth of a spanning tree