cs2223 Class 17

[WPI] [cs2223] [cs2223 text] [News] [Syllabus] [Classes]

cs2223, D97/98 Class 17

More on N-digit integer multiplication

We made a few more comments about the divide and conquer technique for N-digit integer multiplication. The numbers need not bee the same size. Look at several cases:

Both numbers are of the same length

This is the divide and conquer algorithm we we analyzed in Class 14. In that analysis, we showed that the algorithm we learned in grade school for multiplying two N-digit numbers is inherently of order O(N²).

We can split each number into two halves, each of size N/2, so we can use a divide and conquer technique. Four multiplies are required at each step. That produced a recurrence relations whose solution is still of order O(N²).

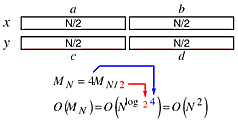
Figure showing the recurrence relation is M(N) = 4 * M(N/2). The solution is O(M(N)) = O(N ^ log (base 2; 4)) = O(N^lg4) = O(N^2); There are arrows showing how the 4 and 2 in the recurrence relation M(N) = ->4<- *M(N/ ->2<-) lead directlyto the 4 and the 2 in the order equation O(N^log(base ->2<-; ->4<-))

By rearranging the terms to reduce the number of multiplications to three, we also reduced the order of the algorithm.

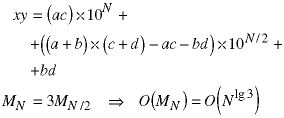
xy = (ac) * 10^N + ((a+b) * (c+d) - ac - bd) * 10 ^ (N/2) + bd; M(N) = 3*M(N/2) -> O(M(N)) = O(N ^ lg3)

One of the numbers is one-digit long

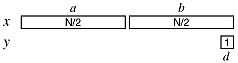
When one of the numbers is of length one, we are back to the case of grade-school multiplication. We can still use the divide and conquer algorithm to reduce this to a sequence of single-digit multiplications. Our analysis shows that it is linear in N.

Figure showing x of length N having two parts, a (the high-order N/2 digits) and b (the low-order N/2 digits). The number y is a single digit, represented by d, which is of length 1 digit.

One of the numbers is one-half the length of the other

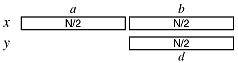
When one of the numbers of one half the length of the other number, we can still find a recursive divide and conquer algorithm which is linear in N.

Figure showing the N-digit number x where a represents the high-order N/2 digits and b represents the low-order N/2 digits. The N/2 digit second number y is represented by d.

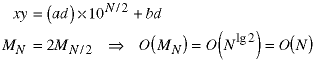
xy = (ad) * 10 ^ (N/2) + bd; M(N) = 2 * M(N/2) -> O(M(N)) = O(N ^ lg(2)) = O(N)

Conclusion

Thus we suspect we can use divide and conquer techniques to create an algorithm which is linear in N, the length of the longer number, when the shorter number has length between one and N/2 and which grows to order O(N^lg3) when when the shorter number has length between N/2 and N. Many commercial implementations of algorithms have this adaptive quality - different algorithms or sub-algorithms are used depending on the detailed characteristics of the data.

Can you devise a multiplication algorithm which works optimally for all possible integer lengths?

Hints

If the smaller number is smaller than N/2, just add enough leading zeros to make it of order N/2, for which we have shown a linear algorithm.

If the smaller number is larger than N/2, we can divide keep the division between the two halves at N/2. Then

Suppose the numbers are of different length, but both are even numbers. We can still use the usual divide and conquer analysis:

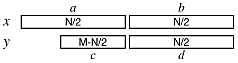
Figure showing the N digit number x in which a represents the high-order N/2 digits and b represents the low-order N/2 digits. The M digit number y is made up of c which represents the (M - N/2) high-order digits and d which represents the N/2 low order d

The lowest halves, b and d, remain the same size at each level of recursion. However, at some recursion level, the c portion will be of size 1 and then zero at the next level. So, at some point the algorithm has to switch from the O(N^lg3) algorithm to the O(N) algorithm. Think about how to detect when the change is necessary.

How about the case when N is neither odd nor a power of two? It is important that the two lowest halves be the same size (or we cannot combine the terms to reduce the number of multiplications from four to three). But, we can use this fact which works in integer math.

This is true in integer math for all integral values of N, both even and odd. Further, the second term on the left is always the same size as or larger than the first on the left. So, we can use these values to divide up the numbers into "halves".

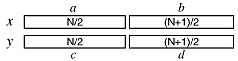
Figure showing two N-digit numbers x and y. The first comprises two parts, a represents the high-order N/2 digits and b represents the low-order (N+1)/2 digits. Similarly, c and d represent the high-order N/2 digits and the low-order (N+1)/2 digits of y.

The parentheses have to be kept as shown. In integer math, these quantities are not necessarily the same (can you prove it?)

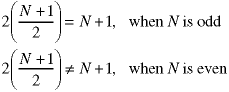
2 * ((N+1)/2) = N+1 when N is odd; but, 2 * ((N+1)/2) != N+1 when N is even.

The proper analysis of this alrogithm requires the use of floor and ceiling functions. If you wish to learn more, look for a discrete mathematics or algorithms text which talks about the floor and ceiling functions. Many algorithms use different variations when the size of the data are odd or even, for example the exponentiation algorithm in Section 7.7 of the text.

Dynamic Programming - Efficient Calculation of Recursion

Dynamic programming algorithms are based on recursion and optimization. In this class we looked at one problem with recursive algorithms - calculation efficiency.

The fibonacci sequence is a sequence of integers which appears frequently in the analysis of algorithms.

The sequence is defined recursively:

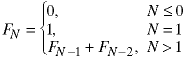
F(N) = 0 when N <= 0; F(N) = 1 when N = 1; F(N) = F(N-1) + F(N-2) when N > 1

There are many ways to implement this algorithm. They differ widely in their computational efficiency, the amount of time required to calculate the N-th term in the sequence.

Note, the code for all of these examples is located in the

Recursive function with no memory

The fibonacci sequence can be calculated by means of a recursive function:

long int fib(int n) // Fibonacci sequence
	{
	if (n <= 0) return 0;
	if (n == 1) return 1;
	return fib(n-1) + fib(n-2);
	} // end fib()

This function is short and elegant, but the computational times can be excessive. A program which implements this algorithm is contained in the CCC directory

/cs/cs2223/classes/class17/class17a.C

The attached script file shows that the execution time grows very rapidly. That is because the number of function calls required to calculate F_N is F_N, a rapidly-growing number.

Analytical Calculation

An analytical solution for the fibonacci recurrence relation based on the method of undetermined coefficients is shown is shown in recurrence relations notes on the Notes page.

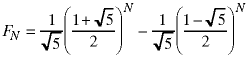
F(N) = (1/sqrt5) * ((1 + sqrt5) / 2) ^ N - (1/sqrt5) * ((1 - sqrt5) / 2) ^ N

Because of the square roots, doubles are used instead of long ints.

double fib(int n) // Fibonacci sequence
	{
	const double sqrt5 = sqrt(5.0); // constants
	const double phi1 = (1 + sqrt5) / 2.0;
	const double phi2 = (1 - sqrt5) / 2.0;
	return (pow(phi1,n) - pow(phi2,n)) / sqrt5;
	} // end fib()

A program which implements this algorithm is contained in the CCC directory

/cs/cs2223/classes/class17/class17b.C

The attached script file shows that the execution time is dramatically improved.

Functions with memory

Whatever algorithm is used to calculate a fibonacci number, there is no reason to do the calculation more than once. A typical dynamic programming technique is to create an array of values and fill it only as far as is needed. This function stores fibonacci numbers in an array and extends the array only when a value is needed which is larger than any calculated in the past. Note that this is an exact calculation using objects of the class n_int introduced in Class 2.

n_int fib(int n) // Fibonacci sequence
	{
	static n_int fib[FIB_MAX + 1]; // be careful, this can become BIG
	static int first_time = 1;
	static int size = -1; // the last value calculated
	if (first_time) // initialize the array
		{
		(fib[0]).make(0);
		(fib[1]).make(1);
		size = 1;
		first_time = 0;
		}
	if (n > size) // calculate only what is needed, but remember it
		{
		for (int m = size+1; m <= n; m++) fib[m] = fib[m-1] + fib[m-2];
		size = n;
		}
	return fib[n];
	} // end fib()

A program which implements this algorithm is contained in the CCC directory

/cs/cs2223/classes/class17/class17c.C

The attached script file shows that the algorithm takes a while to calculate the values in the array, but once a number has been calculated, subsequent calls for the same value are quite fast. The price of this speed is the memory required to store the array.

Random Selection

In class, a great deal of interest was expressed about the method used for selecting which problem is graded. A copy of the program used to perform the selection has been placed in the CCC directory

/cs/cs2223/util/grade.C

This program uses the random number generator to produce a number between 1 and the number of the last problem in the set. It runs 15 times (to show there is no bias) before the actual value is chosen.