cs2223 Class 15, Quicksort Analysis

[WPI] [cs2223] [cs2223 text] [News] [Syllabus] [Classes] [Class 15]

cs2223, D97/98 Class 15, Quicksort Analysis

This is the detailed calculation of the average complexity of the quicksort algorithm, as mentioned on the Class 15 page. The goal is to calculate the solution of this recurrence relation:

E<T(N)> = N + (1/N) * sum(K=1->N; [T(K-1) + T(N-K)]

Write out some of the terms in the summation:

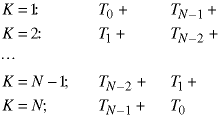
T(0)+T(N-1) {K=1 terms}; T(1)+T(N-2) {K=2 terms}; ... ; T(N-2)+T(1) {K=N-1 terms}; T(N-1)+T(0) {K=N terms}; The equations are written so the two terms in each of these equations are arranged in columns - the first column corresponding to T(K-1) and the

The two columns are the same but reversed, so we can simplify the summation:

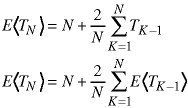
E<T(N)> = N + (2/N) * sum(K=1->N; T(K-1)); E<T(N)> = N + (2/N) * sum(K=1->N; E<T(K-1)>)

The last transformation just uses an important propery of averages: the average of average values is the same as the average of the original values. Thus we can get rid of the expected value notation and remember that our symbols refer to the average values.

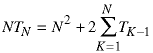
N*T(N) = N^2 + 2*sum(K=1->N; T(K-1))

We also multiplied both sides of the equation by N.

To solve the summation, we use a form of the perturbation method introduced in Class 11. We change the limits on the summation in the usual way.

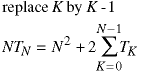
replace K by K-1; N*T(N) = N^2 + 2*sum(K=0 -> N-1; T(K))

The previous term in the sequence is:

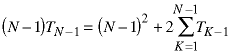
(N-1) * T(N-1) = (N-1)^2 = 2*sum(K=1 -> N-1; T(K-1))

Using a transformation of the variable K to change the limits on the summation, this becomes:

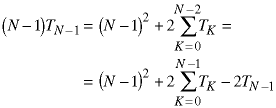
(N-1) * T(N-1) = (N-1)^2 + 2 * sum(K=0 -> N-2; T(K)) = (N-1)^2 + 2 * sum(K=0 -> N-1; T(K)) - 2*T(N-1)

We now have two equations with the same summation. Subtract the equations:

N*T(N) = N^2 + 2*sum(K=0 -> N-1; T(K)) - [(N-1)*T(N-1) = (N-1)^2 + 2 * sum(K=0 -> N-1; T(K)) - 2*T(N-1)]; N*T(N) - (N+1)*T(N-1) = 2*N - 1; T(N) - ((N+1)/N) * T(N-1) = 2 - 1/N

This recurrence relation is first-order and linear but the coefficients are not constant, so we use the Method of Summing Factors in the Recurrence Notes with these values:

The initial condition says that an empty array takes no time to sort. We will need the products of the ,b_n

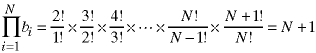
prod(i=1 -> N; b(i)) = 2!/1! * 3!/2! * ... * N!/(N-1)! * (N+1)!/N! = N+1

Now we can use the general form of the summing factor to find the solution:

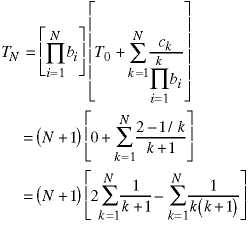
T(N) = prod(i=1 -> N; b(i)) * (T(0) + sum(k=1 -> N; c(k) / prod(i=1 -> k; b(i))) = (N+1) * (0 + sum((2 - 1/k) / (k+1))) = (N+1) * (2 * sum(k=1 -> N; 1 / (k+1)) - sum(k=1 -> N; 1 / (k * (k+1))

The first summation can be solved using the usual change of variables and the definition of the Harmonic sequence:

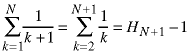
sum(k=1 -> N; 1 / (k+1)) = sum(k=2 -> N+1; 1/k) = H(N+1) - 1

The second summation is even smaller than this so the above equation represents an upper bound on the part of the solution in square brackets. We can continue further by using partial fraction expansion:

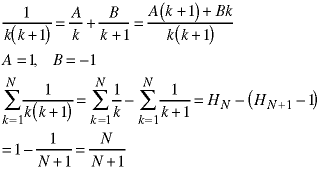
1/(k * (k+1)) = A/k + B/(k+1) = (A*(k+1) + B*k) / (k * (k+1)); A=1, B=-1; sum(k=1 -> N; 1/(k*(k+1)) = sum(k=1->N; 1/k) - sum(k=1->N; 1/(k+1)) = H(N) = (H(N+1) - 1) = 1 - 1/(N+1) = N/(N+1)

Combining everything, we obtain the solution:

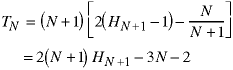
T(N) = (N+1) * (2 * (H(N+1) - 1) - N / (N+1)) = 2*(N+1)*H(N+1) - 3*N - 2

To find the order of this solution, use the approximation for the harmonic series which we introduced in Class 4:

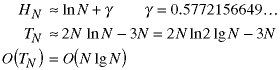
H(N) about= ln(N) + gamma, gamma = 0.5772156649...; T(N) about= 2*N*lg(N) - 3*N = 2*N*ln(2)*lg(N) - 3*N; O(T(N)) = O(N*lg(N))