[WPI] [cs2223] [cs2223 text] [News] [Syllabus] [Classes] 

cs2223, D97/98 Class 14

Note: This page contains an attached Excel spreadsheet. A zip version is also atached for those whose browsers do not reliably download spreadsheet files.

Divide and Conquer Algorithms

This class was an introduction to divide and conquer algorithms. The main charaseristic of divide and conquer algorithms is that the problem is broken into smaller parts which are solved separately. Then the partial solutions are combined to produce the final solution.

The program to add N-digit integers which we showed in Class 2 is an example of a divide and conquer algorithm. In that algorithm, the problem of multiplying large numbers was turned into a successive addition of single-digit numbers, which is somewhat simpler. The algorithm was linear with n.

The most interesting case is when divide and conquer techniques both simplify the algorithm and speed it up.

Search a Binary Search Tree

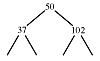
A binary search tree is one which has been constructed - or sorted - so that each node has this property: everything in the node's left subtree has a lower value and everything in the node's right subtree has a higher value (the case of duplicate values is easy to handle, but we won't do that here).

If we are searching for a number less than 50, it will be in the root's left subtree; a number greater than 50 will be in its right subtree, etc. Note the property is recursive, which allows us to write a recursive search algorithm:

int is_int_tree(int number, tree_type tree, index_type index)
		// return 1 if the number is in the tree, 0 if not
	{ // this is pseudo C, C++ so we won't specify those two types
	if (number == tree[index]) return 1; // found it
	// calculate the indices of the left and right children
	if (number < tree[index]) the number, if it exists, will be left
		if (left) return(number, tree, left) // check for node first!
		else return 0; // it's not in the tree
	if (number > tree[index]) the number, if it exists, will be right
		if (right) return(number, tree, right) // check for node first!
		else return 0; // it's not in the tree
	}

This algorithm was written to be symmetrical - for easier understanding - but it makes a few more comparisons than necessary. Since the algorithm advances downward one level at each recursion, the function is called about O(lgn) times, where n is the number of nodes in the tree. This is the average case. The best case - when the root is the number being sought - is O(1). The worst case - when the number is not in the tree and the tree is completely unbalanced - is O(n)

Multiplication of N-Digit Integers

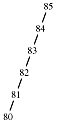
Integer multiplication can be performed using a divide and conquer technique. Decimal notation is just a shorthand for a linear equation:

Note that the largest exponent, 3, is one less than the number of digits, N=4. When we multiply two of these N-digit numbers,

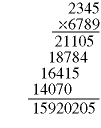
it takes O(n²) single-digit multiplications and O(n²) single-digit additions to find the product. Suppose we break the problem into four smaller problems, each involving the multiplication of numbers with N/2 digits:

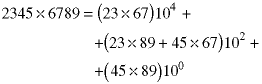
This algorithm can be used recursively to reduce multiplication of two integers of any length to a sequence of single-digit multiplications. This certainly makes the algorithm easier, but it does not reduce the computational complexity. At eash stage in the recursion, the number of multiplications increases by a factor of four and the size of the numbers being multiplied decreases by a factor of two - so the number of single-digit multiplications in each of the multplications goes down by a factor of four. These effects cancel and there is no net reduction in the number of single-digit multiplications. It is still of order O(n²).

Note that the multiplications by factors of ten, shown above, are easy to achieve. Just add the appropriate numbers of zeros to the ends of the intermediate products. This is particulary easy if the integers are stored in stacks, as shown in the Class 2 code; just push the required number of zeros on the stack after the multiplication has been completed.

A Multiplication Algorithm which requires Fewer Single-Digit Multiplications

Each N-digit integer can be written as the sum of four N/2 digit multiplications.

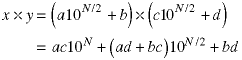
Note, if the numbers are represented in numbering system other than decimal, then that base would be substituted for the 10. Note, again, that four multiplications are required. Note, however, this identity.

This shows that the central product can be replaced by a single product plus two additions of size N/2 numbers and two subtractions of size N numbers. Note, also that ac and bd have to be calculated anyway to produce the outer two products when multiplying x times y. Thus we can form three products of N/2 digit numbers and combine them to produce the product of two N digit numbers.

Example

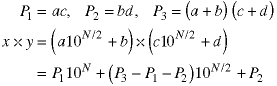
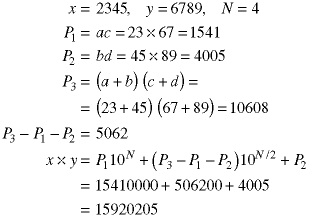
But, this is a recursive algorithm so we can apply it to each of the products, too. Here is the first of the three subproducts.

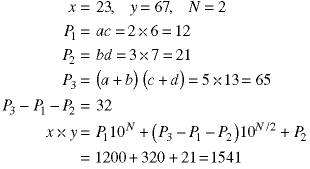
As in this case, the recursion continutes until only single-digit numbers are multiplied.

Analysis of the Multiplication Algorithm

We expect the algorithm shown above to require fewer single-digit multiplications since only three products are formed at each recursive step instead of four. Here is an approximate analysis of the computational complexity.

Let M_N represent the number of single-digit multiplications required to multiply two N-digit integers. Then M_N approximately satisfies this recurrence relation.

The "approximately" means we have ignored additions and subtractions. This can be solved using the technique discussed in Class 8. We also throw away a constant term in this approximate solution.

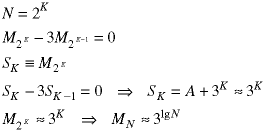
Use this theorm

to rewrite the solution to the recurrence relation.

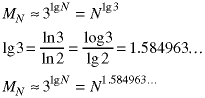
This algorithm is of order O(N^1.584963...). For large values of N, this is substantially less than the original algorithm, which was of order O(N²), as shown in the attached spreadsheet.

[cs2223 text] [News] [Syllabus] [Classes]

Contents ©1994-1998, Norman Wittels
Updated 05Apr98