cs2223 Class 11

[WPI] [cs2223] [cs2223 text] [News] [Syllabus] [Classes]

cs2223, D97/98 Class 11

Perturbation

In Class 10 we showed one way to evaluate a summation - turn it into a recurrence relation and olve it. Here is another way which works with large classes of summations. We will the perturbation method to derive the value of the geometric series. This is the same value whose correctness we proved in Class 6. Begin with the geometric series:

S(n) = sum(k=0->n; a^k) where abs(a) < 1

The perturbation method calculates the next term in the sequence two ways and combines them.

Step 1, Seperate out the last term

S(n+1) = sum(k=0->n+1; a^k) = sum(k=0->n; a^k) + a^(n+1) = S(n) = a^(n+1)

Step 1, Seperate out the first term

S(n+1) = sum(k=0->n+1; a^k) = a^0 + sum(k=1->n+1; a^k) = 1 + sum(k=1->n+1; a^k)

Look at the limits on the last summation. They can be rewritten as two inequalities:

Any constant can be added to both sides of an inequality. If we subtract one from all sides, we can restore the limits on the summation to one and n.

Now replace the k-1 by using a change of variables:

If we make this variable change, the above equation can be written as

S(n+1) = 1 + sum(v=0->n; a^(v+1)) = 1 + a*sum(v=0->n; a^v) = 1 + a*S(n)

Step 3, Combine the equations fromt he two steps

Equate the equations we derived in the two step to complete the derivation

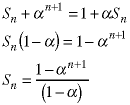
S(n) + a^(n+1) = 1 + a*S(n);
S(n)*(1-a) = 1 - a^(n+1);
S(n) = (1 - a^(n+1)) / (1-a)

See if you can use this method to verify the summation we solved in Class 10,

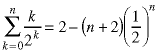
sum(k=0->n; k/2^k) = 2 - (n+2)*(1/2)^n

Greedy Algorithms

In Class 10 we showed how a greedy algorithm can be used to calculate the best way (fewest coins) to make change. Unfortunately, this greedy algorithm - as all greedy algorithm - can fail when applied to problem which require a more sophisticated algorithms. Look at the problem of making change of 26 using coins in denomination 11, 7, 5, and 3. A greedy algorithm, will use two of the 11 coins, which leaves a remainder of 4, which cannot be paid using the four coin denominations. There is a solution - one of each of the four coins add us to 26 - but that solution will not be found by a greedy algorithm.

Printer Queuing

Consider a printer which is attached to a queuing device. Assume the jobs waiting to be printed are numbered and the print time is know for each:

Job time

n t_n

1 3

2 1

3 2

4 7

Suppose we wish to minimize the total waiting time, which we define as the sum of the waiting times for eachof the jobs. For example, if we print the jobs in the order shown above, the total waiting time will be:

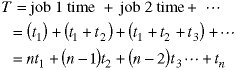
T = job 1 time + job2 time + ... = (t1) + (t1+t2) + (t1+t2+t3) + ... = n*t1 = (n-1)*t2 + (n-2)*t3 + ... + tn

Notice that the first job time t1 is multiplied by n but the last job time t_n is multiplied by 1. The minimum wait time strategy is to multiply the smallest time by n and the longest print time by 1. Thus, the jobs should be printed in order of increasing printing jobs.

The source code for a program which calculates all posible print times for the set of four job times shown above is contained in the CCC directory

/cs/cs2223/classes/class11/

and the attached script shows its operation.

Important note: The source code directory contains a new version of headers.h. The standard template library <iomanip> has been added to this version. Without that additional STL, this code will not properly compile on some systems.