cs2223 Class 10

[WPI] [cs2223] [cs2223 text] [News] [Syllabus] [Classes]

cs2223, D97/98 Class 10

More on Heaps

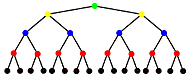
In Class 9 we talked about the algorithm used to turn an array into a heap, or to restore the heap property. Here is an approximate analysis of the order of the process. For simplicity, look at the case where the number of elements in the heap is one less than a power of two - 31 in this case.

Diagram of a complete binary tree of height 5. There are no empty spaces in any row so the tree contains 31 nodes

All of the leaves are at the same height - 0 so the sifting starts one row up. There are eight nodes which, in the worst case, swap once in the downward sift. In the next row, there are four nodes which sift downward twice, in the worst case, and so forth. The worst case number of swaps is:

In general, for a heap of height H - which contains about 2^H+1 nodes - the worst case number of swaps is:

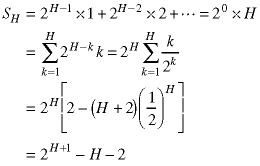
S(H) = 2^(H-1)*1 = 2^(H-2)*2 + ... = 2^0 *H = sum(k=1->H; 2^(H-k)*k) = 2^H*(2 - (H+1)*(1/2)^H) = 2^(H+1) - H - 2)

A method for solving the summation is shown on an attached page. For the case shown above, this gives us the right answer.

The result can also be expressed as a function of the number of items in the heap, n.

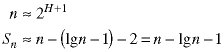
n about= 2^(H+1);
S(n) = n - (lgn -1) -2 = n - lgn - 1

This shows that the operation of turning an array of size n into a heap is of order O(n), in the worst case.

Greedy Algorithms

A greedy algorithm is one which always uses the maximum amount of a resource. A classic example is that of making change. Suppose you are using American money and want to give someone $6.67 in change. You start with the largest denomination available ($1000 bills) and work your way down through the denominations. At each step, use that denomination to reduce the total as much as possible:

quantity

denomination
value

0

$1000
0.00

0

$500
0.00

0

$100
0.00

0

$20
0.00

0

$10
0.00

1

$5
5.00

1

$1
1.00

2

$0.25
0.50

1

$0.10
0.10

1

$0.05
0.05

2

$0.01
0.02

total
6.67

Although greedy algorithms are relatively easy to implement, they sometimes fail. For example, if a monetary system has 2 and 3 coins but no 1 coin, then the correct way to make change of 7 is with 1x3 + 2x2, but a greedy algorithm will subtract 2x3 and then have no way of paying out the remaining 1.

quantity	denomination	value
0	$1000	0.00
0	$500	0.00
0	$100	0.00
0	$20	0.00
0	$10	0.00
1	$5	5.00
1	$1	1.00
2	$0.25	0.50
1	$0.10	0.10
1	$0.05	0.05
2	$0.01	0.02
	total	6.67