cs2223 Class 7

[WPI] [cs2223] [cs2223 text] [News] [Syllabus] [Classes]

cs2223, D97/98 Class 7

More on Proofs

We looked at a few examples which use the techniques discussed in Class 6.

Sorting

Prove that no algorithm can be developed to find the minimum value in an array of random values of length n withcompares. Use proof by contradiction. Assume that an algorithm has been developed which correctly finds the minimum value with compares. Now look for a contradiction.

Since we are interested in behavior with large values of n, assume that n>4.

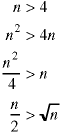
n>4;
n^2 > 4n;
n^2 / 4 > n;
n/2 > sqrt(n)

Thus our algorithm, which uses compares, certainly uses fewer than n/2 compares. But comparison is a binary operation, so the algorithm can compare the values of fewer than n array elements. But the array contains n elements, so the algorithm ignores at least one value. If that value is changed to be the smallest in the array, the algorithm will erroneously show that another value is the minimum. This contradicts our assumption, proving the initial premise.

Factoring of Polynomials

Prove thatevenly dividesfor all values of n and all values of . Use proof by induction.

Basis step:

Inductive step: Assume that evenly divides for some step n. Look at the next step.

Both terms on the right can be evenly divided by , the first term by the inductive assumption and the second because it is the basis step. This completes the proof.

Intersecting Lines

Prove that all non-parallel lines in a plane intersect in the same point. This seems not to be correct - a triangle is a simple counterexample - but we'll complete the proof anyway.

Basis step: It is not meaningful to talk about zero lines intersecting in a common point (no lines means no points) nor about one line intersecting in a common point (all points in the line are in the line; there is no single, common point), so we begin with the case n=2. Two non-parallel lines intersect in a common point, confirming the basis step.

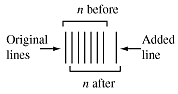
Inductive Step: Assume that a set of n lines all intersect in a common point. Look at the n+1 case. Group the n lines into a single line and a group of n-1. Group those n-1 lines with the new line, forming a new group of n lines - in the figure below, the lines are shown parallel because that is easier to draw, but they really all intersect in the same point. By the inductive assumption, this group of n lines intersect in a common point. Since that is the common point of the original n lines, all n+1 lines intersect in a common point. This completes the proof.

Figure showing n grouped lines plus an 'extra' line; then the lines are regrouped so that the 'extra' line is regrouped with n-1 of the original lines and one of the original lines is now the 'extra'

However, the proof if faulty. Go back to the first step after the basis step, n=3.

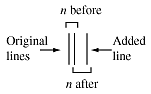
Figure showing two grouped lines plus an 'extra' then the 'extra' is regrouped with one of the original lines to form a group of two with one of the originally-grouped lines becoming the 'extra'

The "group" of size n-1 that we move to group with the new line only has one line in it. We specifically said that a single line has no common point, so the method that we used to show that both groups of n lines have the same common point is wrong when n=3. If we had shown that there were two basis steps - n=1 and n=2 or n=2 and n=3 - then the proof would have been valid for all values on n. However, we used the wrong basis step so the proof is invalid. And, since the "basis step" concept (a common point) does not fit n=1 or n=2, there is no way to patch up this proof. Our notion that the proof was bogus was correct.

Polynomial in n

Prove that the solution to this recurrence relation

Begin by establishing the basis step, n=0.

The basis step has been established. We really should do the inductive step - assume the answer is true for n, show that makes it true for n+1 - but that is a lot of work when dealing with the fourth power of n. Instead, let's just verify the next few terms:

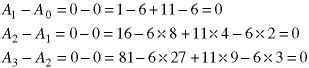
A(1) - A(0) = 0-0 = 1 - 6 + 11 - 6 = 0;
A(2) - A(1) = 0-0 = 16 - 6*8 + 11*4 - 6*2 = 0;
A(3) - A(2) = 0-0 = 81 - 6*27 + 11*9 - 6*3 = 0

The pattern is established so we can declare the proof done.

In fact, this is not a proof, as we can see if we continue one more term:

The point is that a demonstration does not constitute a proof. The difference is between testing a finite number of cases versus proving all cases.

Solution of Recurrence Relations

Be sure to read Section 4.7 of the text and the Recurrence Relations Notes. We will use the solution techniques explained there without the details.

Towers of Hanoi

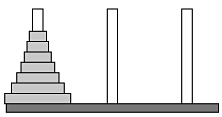
Figure showing three rods with a stack of discs on the left-most rod

This is a classic problem in computer science and it is discussed on p109 of the text.

We want to move a stack of discs from one to another of three rods. The rules of play are: only one disc can be moved at a time; no disc may be placed on top of one which is smaller.

Let M_n be the total number of moves to move a stack of n rings from one rod to another. We looked at the number of steps required to move the n-th ring from the original rod to the empty rod and then move the stack of n-1 rings from the third rod on top of it.

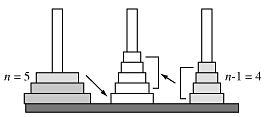
Figure showing n-1 of the discs moved to the right-most rod, the n-th disk moved to the center rod, and the n-1 disks moved from the right-most rod to the center rod to make a stack of size n on the center rod.

From measurements we made in class we concluded that this number of moves is 2^n-1. That lead directly to a recurrence relation for M_n.

The solution to this recurrence relation is:

This is a function which grows very rapidly with n.