Open Questions

1. Does there exist an SI graph G whose complement comp(G) is also SI? Current hypothesis: doubtful since SI graphs show a tendency to consolidate symmetry in a few regions of the graph that is offset by Paths of asymmetry. Also, if [see question 3 below] the ratio of edges to vertices is a fixed constant, then the only graph whose complement has the same property is defined as follows:
   
   Assume |E| / |V| <= k
   |comp(E)| = n(n-1)/2 - |E|
   
   dividing by n (which is |V|) we have:
   
   |comp(E)| / |V| = (n-1)/2 - |E| / |V|
   (n-1)/2 >= |comp(E)| / |V| >= (n-1)/2 - k
   
   but |comp(E)| / |V| must be <= k (our assumption), leaving us with:
   
   (n-1)/2 >= k >= (n-1)/2 - k
   
   which is only true when k >= (n-1)/4, a contradiction if k is a constant. So if |E| / |V| <= k, then comp(G) can't also be SI. 
   
2. Is there a standard recursive algorithm for the G4 embedding?
3. What is the largest number of edges for a SI graph with n vertices? Current hypothesis: 2*n. Is this some constant k? 
4. In a status injective graph, must the two lowest status numbers be adjacent vertices?
5. What is the largest degree vertex in an SI graph?
6. Is there an SI graph that retains its SI property after a new node/edge has been added? YES, but not sure where the graph went.

Solved Questions

1. Question: What is the maximum path extension <v₀,v₁,v₂,v₃, …,v_k> such that deg(v_k)=1, and deg(v_i)=2 for 1 <= i < k) and the graph G may yet be status injective?
   
   
   
   
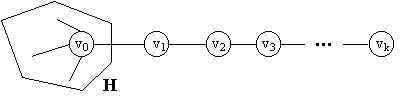
   Answer: Consider a potential SI graph G = (V, E) which is subdivided into H, a subgraph of n vertices, and a path extension of size k emanating from v₀ within H. Note that |V| = n + k. Let the status of vertex v₀ only considering vertices inside H to be s. We shall provide bounds on k and n such that independent of s, the path extension will contain at least two vertices with the same status number. Note: there may yet be vertices inside H whose status is the same as a path extension but we do not have sufficiently powerful techniques to catch these cases.
   
   The status numbers for vertex vi can be calculated as follows:
   

   status (vi) =	(k - i + 1)*(k - i)/2 +	/* contribution from vj to right. */
   	i*(i + 1)/2 +	/* contributions from vj to left. */
   	s + i*(n - 1)	/* contributions from H-v0. */

   Note that the contributions for vertices v_j to the left of v_i include v₀. Since n, k, and s are constant, we redistribute to reach the following quadratic equation:

       i² + (n – k – 1)*i + (k² + k + 2s)/2

   
   For this equation, when k = n-1, the middle term vanishes and the status numbers for the vertices on the path extension are of the form i²+c, which is monotonically increasing, thus ensuring no duplicate status numbers within the path extension. Conceptually, one can envision a positive parabola centered at the y-axis. For values of k<n-1, the parabola shifts to the left and the equation above continues to be of the form i²+c. However, when k>n-2 then the parabola shifts to the right and there will be two values of i that compute to the same value, thus proving that given an SI graph with n+k vertices, there can be no path extension of size k or greater. QED. (Word Document).

2. Can a SI graph have only vertices of degree > 1? Yes! Discovered the first one manually on May 31 2002 (check it out)!

George Heineman (heineman@cs.wpi.edu)
08/29/06 10:42 PM