8.1 Comparison of Algorithms

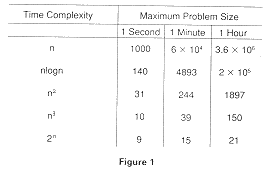
Optimization can't speed up a really slow algorithm by large factors. Figure 1 shows, within multiplication by a constant, the amount of data which can be processed relative to a base value. If 1000 "widgets" can be processed in linear time, then only 140 can be processed using an algorithm which is O(nlogn), etc.

Suppose we are able to optimize a program to produce a speed-up of a factor of 10(an ambitious improvement).

If we let S = problem size, then after a speed-up by a factor of 10:

 
 	Complexity		Problems Size
 
 	Linear (n)		10S
 	nlogn 			10S (for large S)
 	n² 			3.16S
 	n³ 			2.15S
 	2ⁿ 			S + 3.3

We can conclude from this that bad algorithms are not helped much by optimization.

However, clever optimizations of clever code may not improve things either. Knuth (1971) presented an amusing discussion in which he referred to an algorithm which he had developed many years ago which translated a complicated expression to fewer instructions than some other people's algorithm. Years later, he realized that programmers rarely used such complicated expressions, and it isn't worth the compiler's time to optimize them.